ch04 前馈神经网络

4.1 神经元

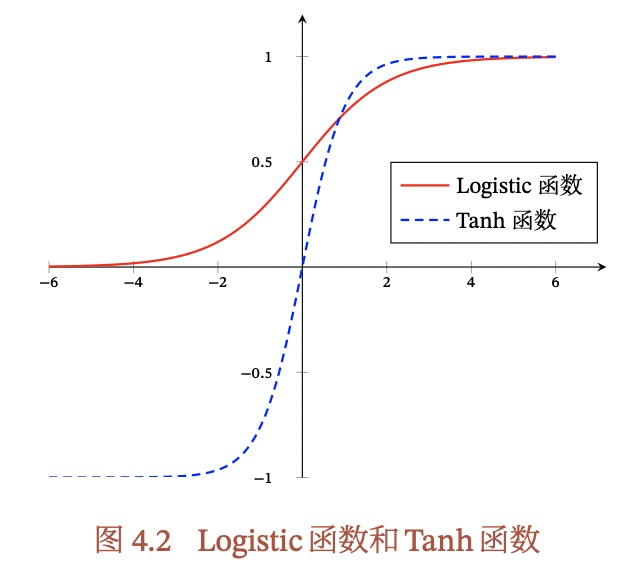
画出logistic函数和tanh函数的图形，哪个是非0中心化的，非0中心化会有什么问题？

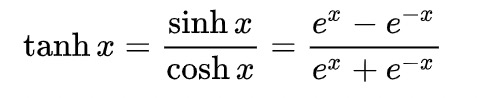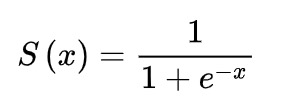logistic函数是非0中心化的，非0中心化的输出会导致其后一层的神经元的输入发生偏置偏移（Bias Shift），并进一步使得梯度下降的收敛速度变慢。简单的说，就是所有参数的都是统一方向的，要么都是正，要么都是负，从而导致产生zig-zag path，导致收敛速度变慢。
以cs231n 2017 Training Neural Networks, part I 为例，假如我们的损失函数为L，预测函数为下图的，那么在反向传播时，根据链式法则，每个参数w的更新公式为：

lr是学习率，通常是一个小的正数，右边的wi是上一轮更新的结果，对任意的wi，都是一样的，可是看做一个常数，xi是上一层神经元的输出，在选择sigmoid作为激活函数时，xi一定是(0,1)之间的数。所以，对于所有的wi来说，他们更新要么都是正值，要么都是负值，这取决于的正负性，也就是上图右边的绿色部分，假如此时最优模型的wi是有正有负的，那么更新就只能走Z字型，从而降低了收敛速度。

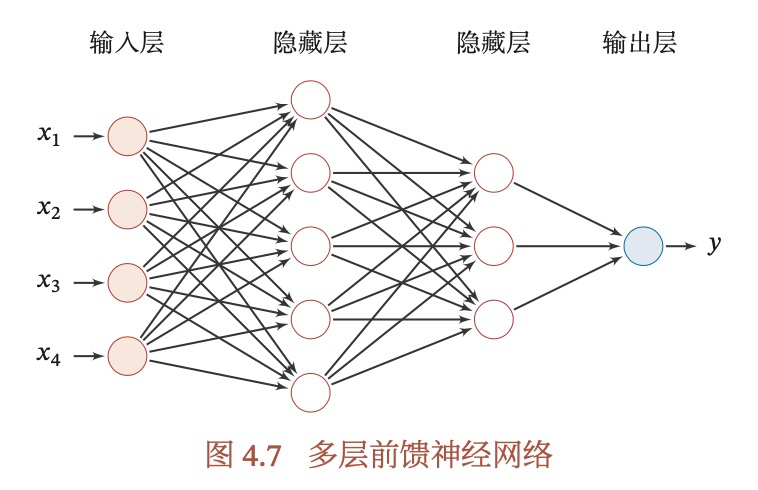
4.3 前馈神经网络（多层感知机Multi-Layer Perceptron）

什么是自回归模型？

用一个变量yt历史的信息来预测自己，是一类常用的时间序列模型。也可能有其他的输入，但是只要有用y来预测y的，就可以是自回归。

什么是仿射变换？

仿射变换是指把向量从一个空间变换到另外一个空间，实际操作=线性变换+平移，即Ax+b，A是矩阵，x是原向量。仿射变换本质是一种线性变换。
仿射变换可以实现线性空间中的旋转，平移，缩放，3种变换。
具有以下性质：

1. 共线性不变：共线的点，在新空间依然共线
2. 比例不变：不同点之间的距离不变
3. 平行性不变：平行线在转换后依然平行
4. 凸性不变：凸集在新空间也是凸的

   4.4 反向传播算法

   什么是链式法则？

   链式法则是求复合函数导数的一种方法，

   什么是反向传播，举一个例子来说明反向传播？

   cs231n 反向传播notes的中文翻译 cs231n 2017 Introduction to Neural Networks-Backpropagation 对应课程在网易云课堂上有中文翻译

链式法则指的是求某个参数梯度的方法，例如从损失函数逐层求导，直到最里层的权重wi。但是如果你每层都采用链式法则独立求导，那么计算会很复杂，反向传播是把整个前向传播的计算过程分解为不同的计算单元，每个计算单元在计算前向传播的同时，计算自己单元内的梯度。然后在反向传播时，每个参数的梯度等于其到loss路径上的每个单元内部的梯度的乘积，如果有多个路径，再求和。

什么是向量的内积，外积？

假如a=[a1,a2,a3,…,an] b=[b1,b2,b3,…,bn]
内积：又称为向量的点乘，结果是一个实数，可以用来计算两个向量的夹角。


外积：又称为向量的叉乘，结果是一个向量，这个向量正交于a和b，与ab所在的坐标平面垂直，也就是ab平面的法向量。

什么是分母布局，什么是分子布局？

• 分子布局：一个标量关于一个向量的导数写成行向量

• 分母布局：一个标量关于一个向量的导数写成列向量

  向量关于向量的偏导数是向量还是矩阵？什么是雅克比矩阵，什么是Hessian矩阵？

  
  雅可比矩阵是两个向量的偏导数矩阵，Hessian矩阵是两个向量的二阶偏导矩阵。
  

  什么是雅克比矩阵？

  https://www.bilibili.com/video/BV1NJ411r7ja?from=search&seid=10463379635545930332&spm_id_from=333.337.0.0
  https://www.bilibili.com/video/BV18J41157X8?from=search&seid=10463379635545930332&spm_id_from=333.337.0.0

  什么是海森矩阵？

  https://www.bilibili.com/video/BV1H64y1T7zQ?from=search&seid=10166108417139825172&spm_id_from=333.337.0.0

  4.5 自动梯度技术

  除了现在广泛采用的自动微分以外，自动梯度常见的技术有哪几种？

  还有啥？

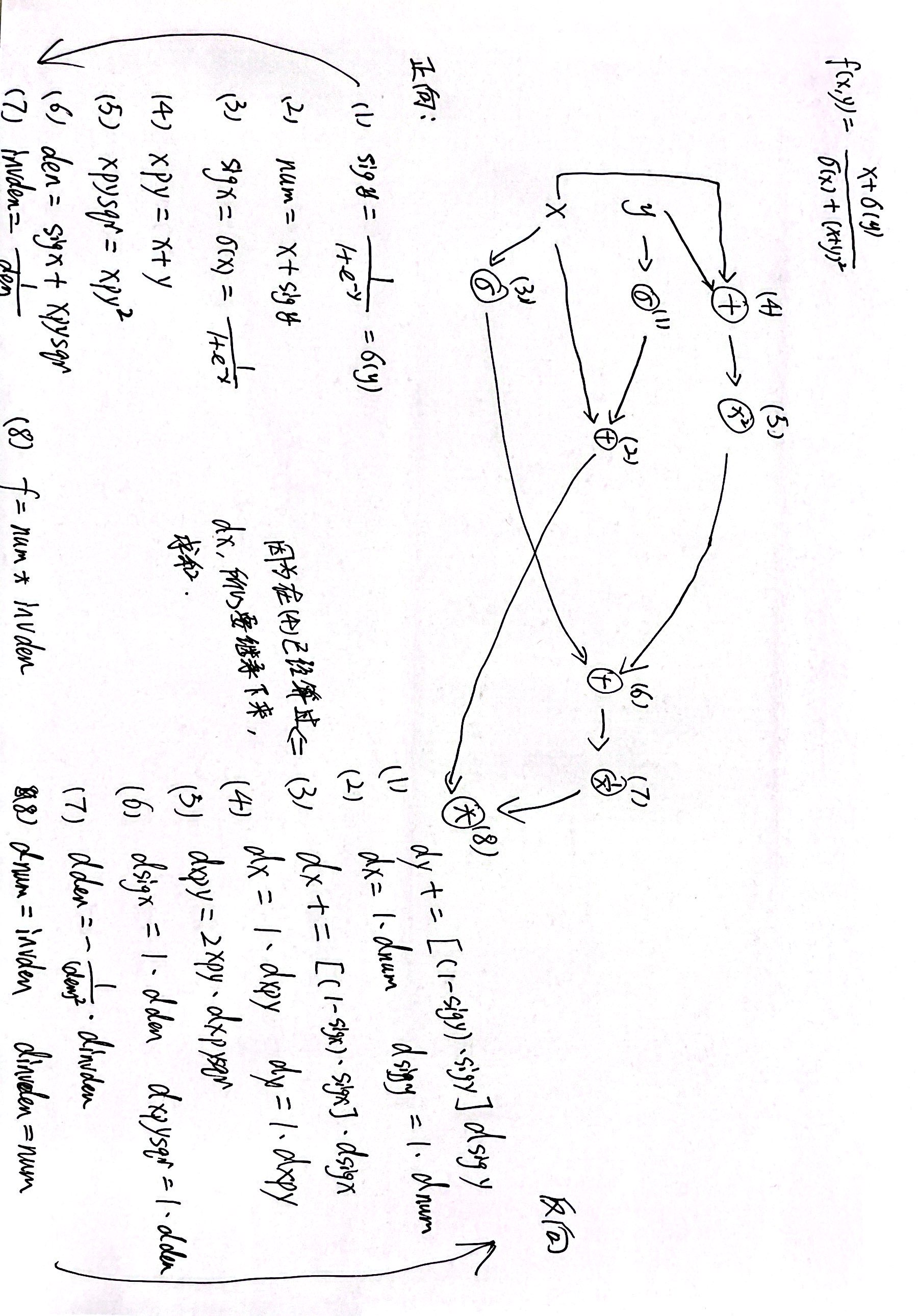
  以下面公式为例，说明自动微分的过程。

  
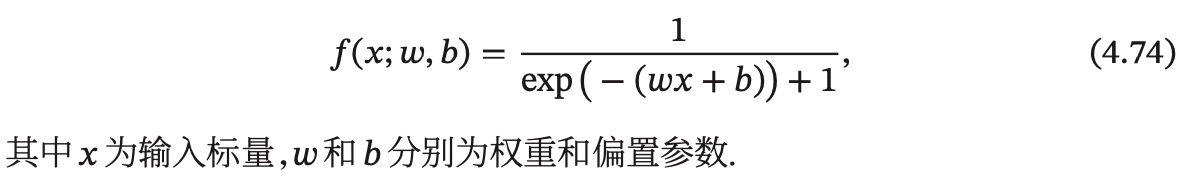
  自动微分的基本原理是所有的计算都可以分解为一些基本操作，如+-*/，sin,cos,log,exp等，然后通过链式法则来自动计算一个复合函数的梯度。如下图是(4.74)的计算图，得到某个导数，只需要对应路径相乘，如果有多个路径，则相加。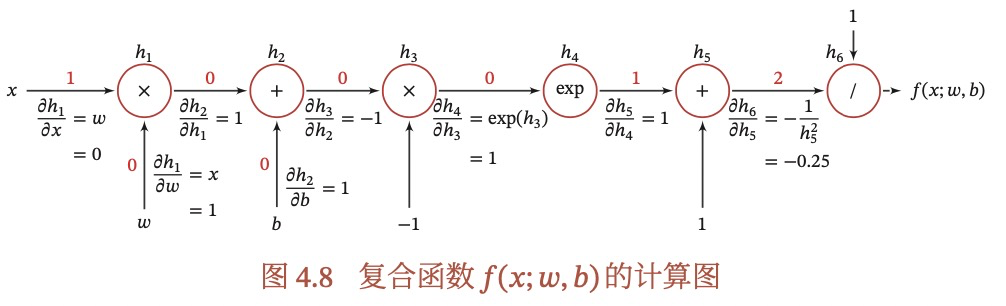
  

  怎么理解静态图和动态图？

• 静态图：程序编译时构建图，之后不能改变，效率高但灵活性差。

• 动态图：程序执行时构建，灵活性高但效率低。

  4.6 优化问题

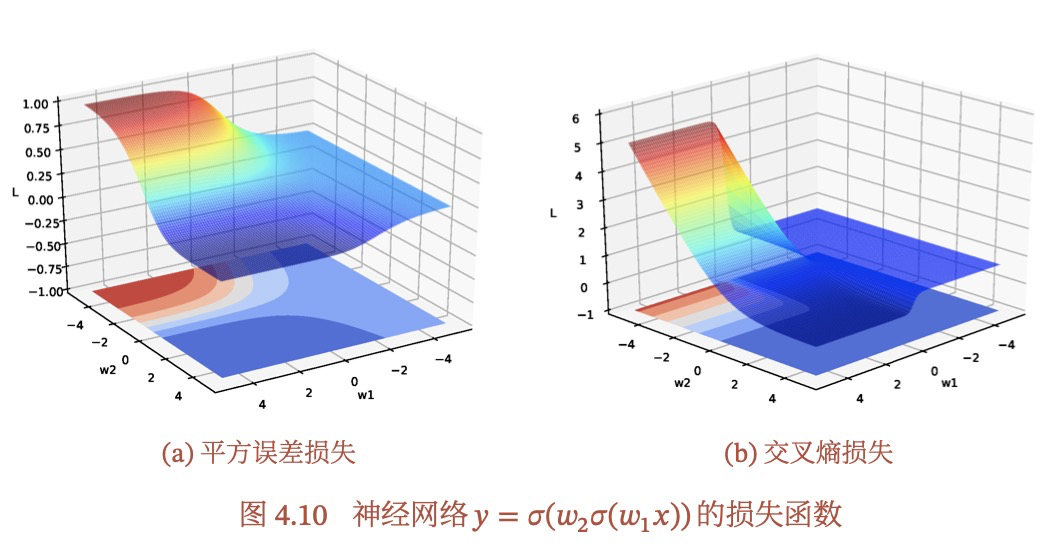
  举例说明，为什么神经网络的优化是非凸优化问题？

  通过简单的举例和画图就可以看出是个非凸优化问题，不一定需要复杂的数学证明，如下图：
  

  什么是梯度消失问题，为什么会有？

  总体来说，梯度消失的产生是因为在反向传播的过程中，梯度会进行连乘，那么如果一直连乘一个小于1的数，梯度的值就会越来越小，导致更新不动，产生梯度消失。如果连乘一个大于1的数，梯度的值就会越来越大，导致梯度爆炸，出现Nan。具体产生的原因可能是因为某些激活函数的梯度性质，如Sigmoid函数，或者是因为参数矩阵的连乘，如RNN中的梯度消失。

  首先，我们来看误差的反向传播公式：
  
  反向传播时，每一层都要乘以该层的激活函数的导数（上式f是激活函数），当使用Sigmoid型函数时：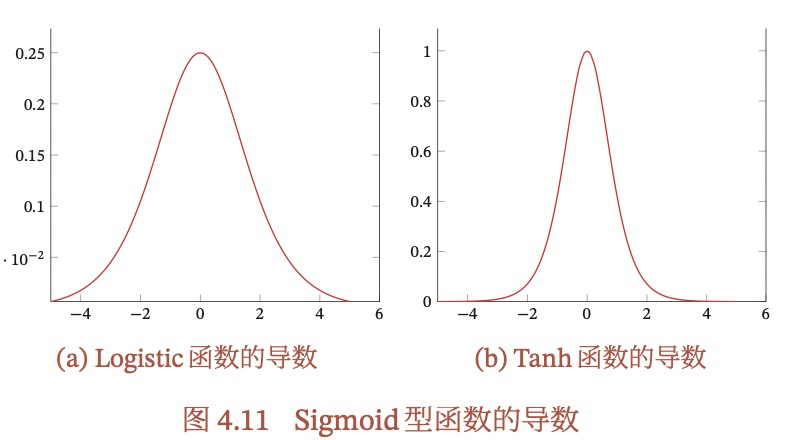
  
  
  由于导数都小于1，尤其在饱和区，甚至接近0，所以误差经过每一层都会不断衰减，当网络层数较深时，梯度就可能接近0，使得整个网络不再更新，这就是所谓的梯度消失问题，也称为梯度弥散问题。
  误差同时还受参数矩阵的影响，如果参数矩阵的初始化不太合理，也有可能发生梯度越来越大的情况，从而发生梯度爆炸。
  其次，在RNN中，也经常会出现梯度消失问题，具体可以见《ch06 循环神经网络》。