ch02 机器学习概述

2.2

损失函数、风险函数，代价函数，期望风险、经验风险、结构风险分别是什么？

1. 损失=风险=代价，损失函数用来衡量模型的好坏
2. 期望风险：理论上的损失，模型与真实分布的差距，永远未知
3. 经验风险：在训练集上的损失

4. 结构风险：带正则化的经验风险

   *损失函数无法求导该怎么样进行优化？

   A: 对于凸函数不可导的情况下，可以使用次梯度。次梯度是个啥？https://www.zhihu.com/question/38846817

   平方损失的公式是什么？可以用于分类问题吗？

   N - 样本数，y - 真实值， y’ - 预测值

5. 如果是多分类，那么每个类别是同地位的，类别之间也是没有连续概念的，所以类别之间的距离没有意义，所以预测值和标签之间的的距离不能反应问题的优化程度。例如：输出空间Y={1,2,3}，某个样本标签为1，如果模型预测为3，那么损失会比预测为2，要大，那显然是不合理的。

6. 如果是2分类问题。假设输出空间只有{-1,1}的情况，那么yy’，即真实标签*预测标签应该是越大越好，但对于平方损失却随着yy’的增大，先减少，再增大，因此不适用于二分类问题，如下图，图中f(x,w)就是y’。

上式能成立，因为我们假设了输出空间为{-1,+1}，因此y2=1。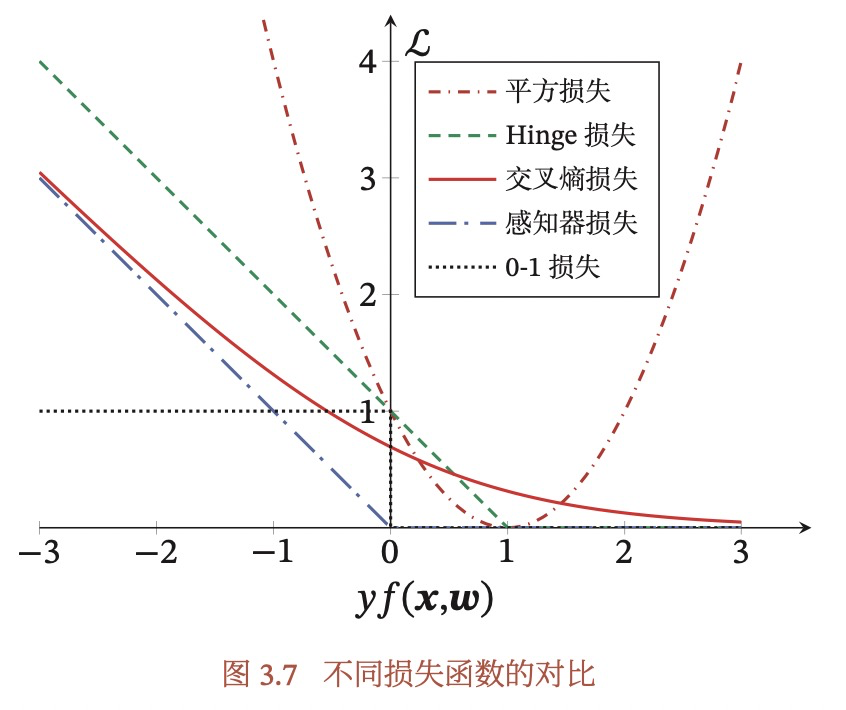

1. 如果输出空间是{0, 1}呢，大部分时候是可以用平方损失作为损失函数的，但是逻辑回归不行。

以下内容主要参考自：Why not Mean Squared Error(MSE) as a loss function for Logistic Regression?
从直观上理解来看，如果一个样本，真实标签是1，预测为0，那么


显然log loss的惩罚更大。
从数学角度看，L_MSE的二阶导如下：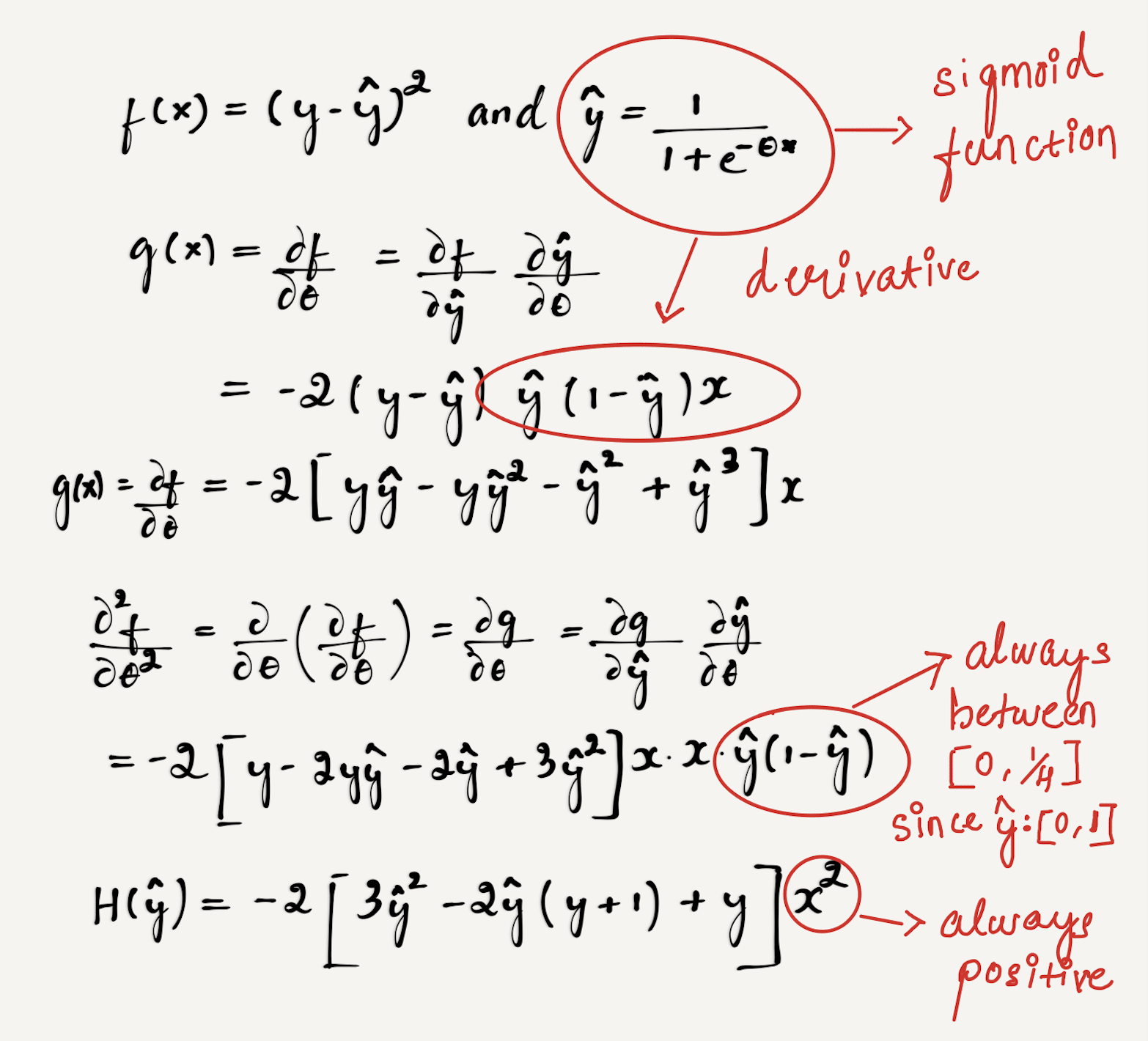

在二阶导的时候，先用代替求导结果，不要着急求出来，然后是可以提取出来的。所以我们需要求的正负性，因为y为[0,1]，所以考虑极端情况：

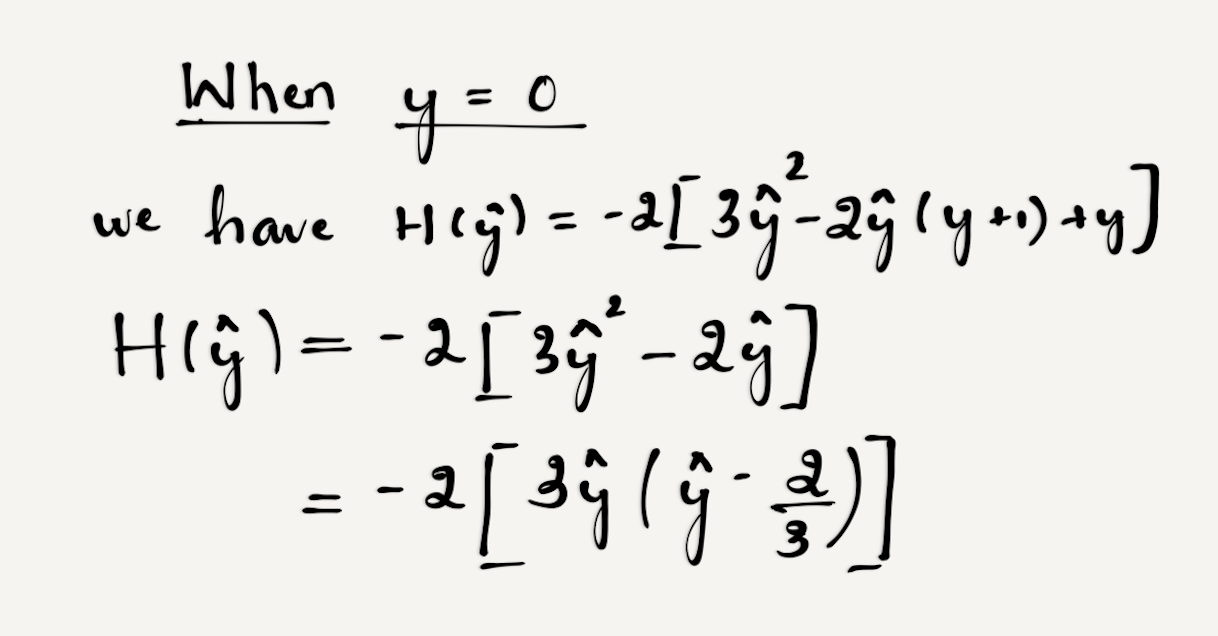
显然，当属于[0, 2/3]时，，此时函数为凸函数（二阶导>=0为凸函数）；当 属于[2/3, 1]时，，函数为非凸。

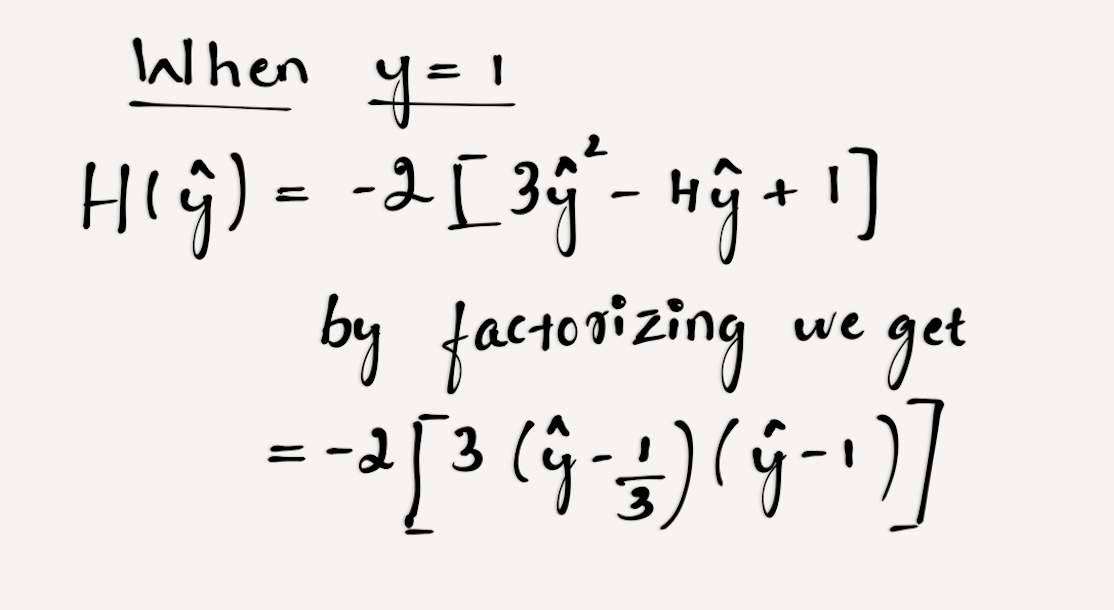
显然，当属于[0, 1/3]时，H(hat y) <=0，此时函数非凸；属于[1/3, 1]时，，此时函数凸。
因此两种情况都表明，L_MSE是一个非凸函数，会陷入局部最优解。如果采用最大似然估计，则Loss函数是高阶连续可导凸函数，就可以通过一些凸优化算法求解，如梯度下降，牛顿法。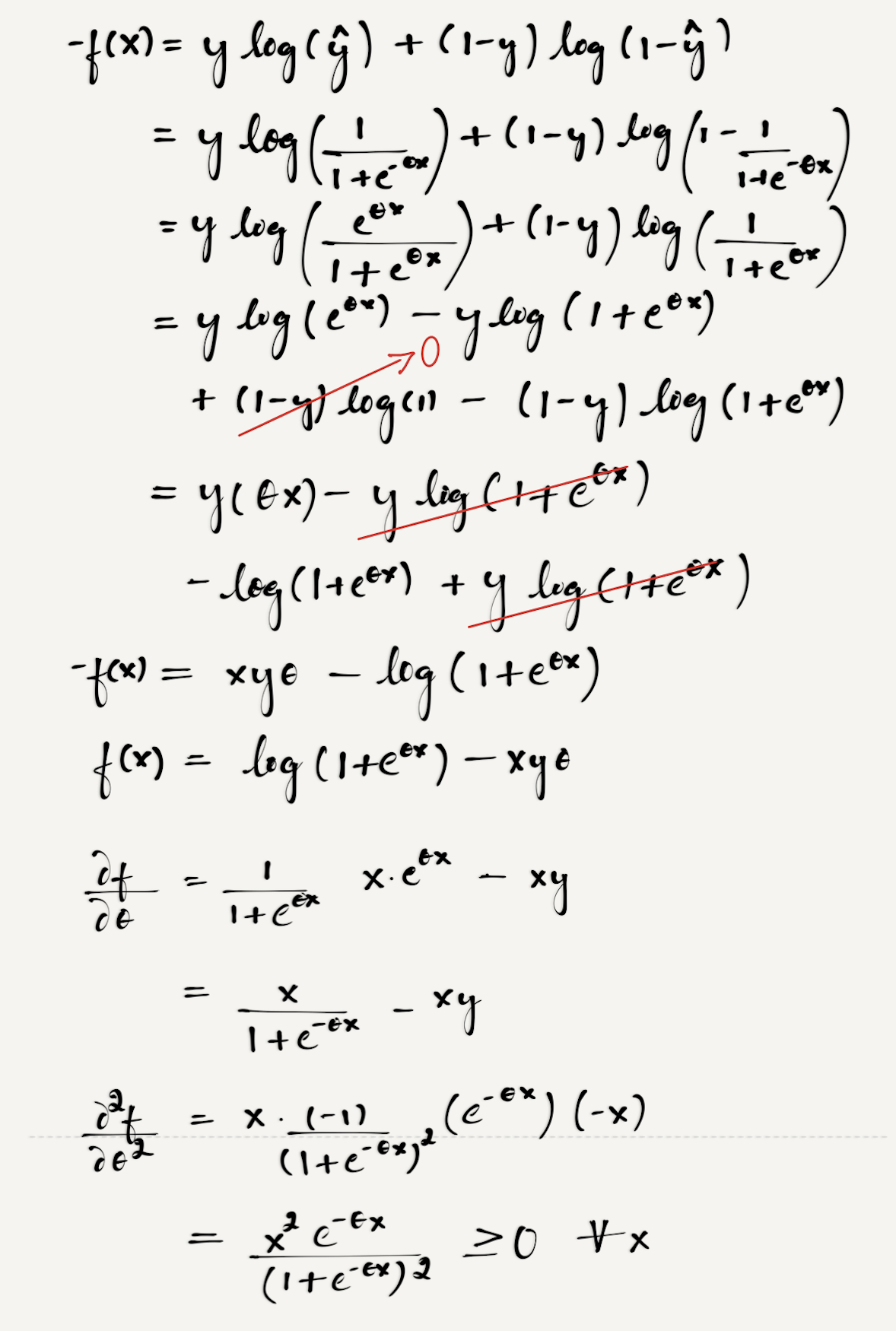

交叉熵损失用在回归还是分类？公式是什么？

交叉熵（cross-entropy）用来衡量两个概率分布的差异，衡量预测概率分布y’能否准确刻画真实的概率分布y，数值越小表示约接近。一般用在分类上，公式为：

y - 真实标签，有c个类别，每个都表示成one-hot形式，只有1个维度为1，其余为0
y’ - 预测标签，是一个在c个类别上的概率分布，即该样本为c个类别的概率，加起来为1
比如对于三分类问题，一个样本的标签向量为𝒚 = [0,0,1]T，模型预测的标签分布为

• y’= [0.1, 0.4, 0.5]T ，则它们的交叉熵为 −(0 × log(0.1) + 0 × log(0.4) + 1 × log(0.5)) = 0.3。
• y’=[0.1, 0.1, 0.8]T，L=-(0 x log(0.1) + 0 x log(0.1) + 1 x log(0.8) =0.1。

显然下面一个概率分布更接近真实值。

什么是对数似然函数？

最大似然，就是求样本出现的最大概率，所以是每个样本出现概率的乘积，为了方便求解，取Log，转化为求和，所以是对数似然。

交叉熵损失函数与对数似然函数有什么区别？

记得上面的交叉熵公式为：

y是一个one-hot向量，只有1个维度是1，其余都是0，因此可以简化为-ylogy’，因为y=1，也就是

这个公式也就是负的对数似然函数。因此交叉熵损失函数就是负的对数似然函数。

*什么是KL散度，JS散度，Wasserstein 距离？

• 交叉熵是按照概率分布q的最优编码对真实分布为p的信息进行编码的长度，定义为：

在给定p,q的情况下，p,q越接近，交叉熵越小，反之越大。

• KL散度(KL-Divergence)，又叫相对熵，是指交叉熵和真实熵的差异，即：

• JS散度是一种对称的衡量两个分布相似度的度量方式：

• wasserstein比较复杂，可以暂时先不了解

  hinge loss的公式是什么?

  这个公式是啥，没看懂？
  y - 真实标签，取值为{-1, +1}
  y’ - 预测标签，实数

  *如何理解从贝叶斯学习角度讲，正则化是引入了参数的先验分布，使其完全不依赖训练数据？

  PRML笔记1-从贝叶斯先验的角度解释正则化
  PRML里应该有关于这个的贝叶斯角度解释。

  什么是过拟合和欠拟合？

  过拟合 - 模型在训练集上表现良好，在测试集上效果不好
  欠拟合- 模型在训练集上表现也不好

  怎么解决过拟合问题？

• 加正则

• 加数据
• 简化模型
• early stop：引入验证集，在验证集上判定模型效果，如果在验证集上错误率不再下降，就停止模型迭代。

  什么是early stop？

  引入验证集，在验证集上判定模型效果，如果在验证集上错误率不再下降，就停止模型迭代。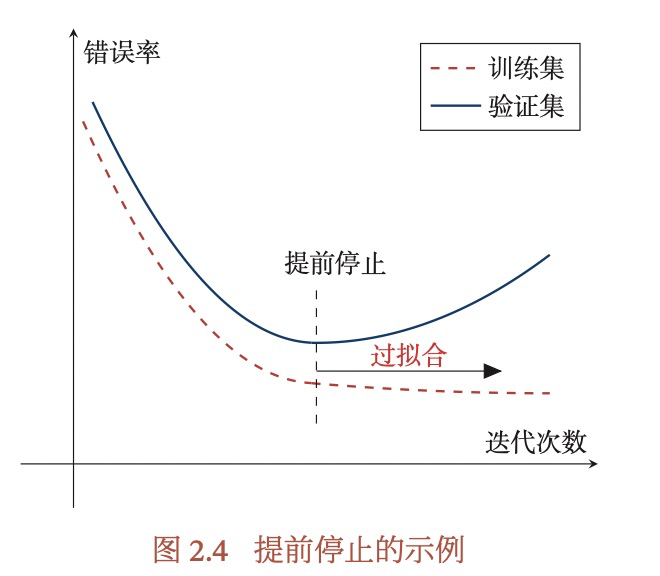
  
  实际是怎么操作的？怎么知道错误率不再下降呢？

  2.3

  什么是最小二乘法？

  以线性模型为例，损失函数为平方损失：

1. 最小二乘法LSM：直接在矩阵上求解w偏导为0时，矩阵的解w。当矩阵X的特征间不是线性相关时，可以先用PCA降维，再用LSM，或采用岭回归方法，给XXT的对角线元素都添加一个常数，使得XXT满秩，岭回归=LSM+L2正则。

2. 最小均方法LMS：通过梯度下降来学习参数。

   什么是似然函数，对数似然，最大似然估计？

   似然函数是关于统计模型的参数的函数。对数似然，是对似然函数取log。最大似然估计是指找到一组参数w，使得似然函数p(x|w)最大。

   似然𝑝(𝑥|𝑤)和概率𝑝(𝑥|𝑤)的区别？

   概率𝑝(𝑥|𝑤)是描述固定参数𝑤时，随机变量 𝑥 的分布情况，而似然 𝑝(𝑥|𝑤) 则是描述 已知随机变量 𝑥 时，不同的参数𝑤对其分布的影响。
   

   最大似然估计的缺点是什么？

   当训练数据比较少时会过拟合。可以引入先验知识，利用贝叶斯公司，将求最大似然估计转化为求参数w的最大后验估计(Maximum A Posteriori Estimation，MAP)。
   

   2.4

   什么是方差和偏差分解？

   假设fD(x)表示单个样本x在不同训练集D上得到的模型，f*(x)表示最优的模型。两者期望的差可以分解为偏差的平方+方差。方差和偏差分解，证明了我们可以通过减少方差和偏差，来优化模型。

   偏差和方差有什么作用？

   偏差(bias)表示模型在不同训练集上的平均性能和最优模型的差距，衡量模型的拟合能力；
   方差(variance)表示模型在不同训练集上的差异，衡量模型是否容易过拟合。
   最小期望错误=最小化（偏差+方差）。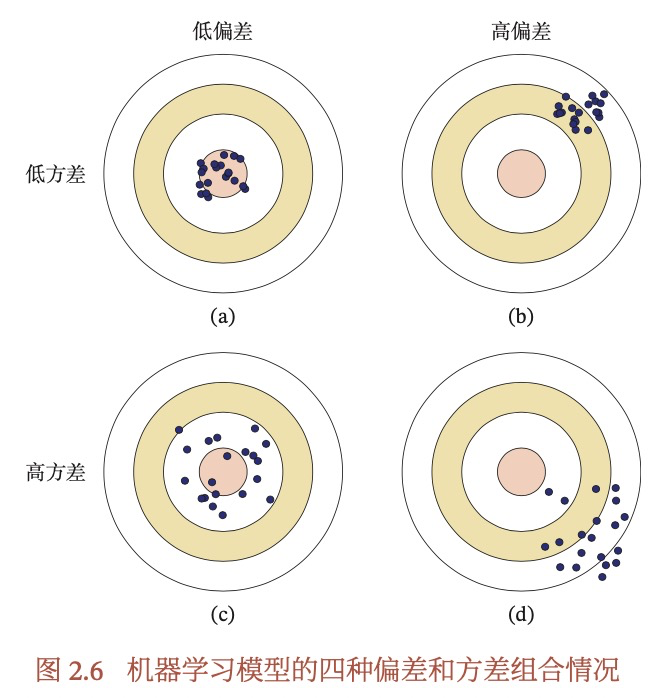
   

   如何减少偏差和方差？

   偏差就是模型欠拟合，学习能力不足，因此可以考虑减少数据，增加模型复杂度（减少正则化程度，或替换更复杂的模型等）。相反，方差表示模型过拟合，因此表现不稳定，可以考虑增加数据，减少模型复杂度或引入先验，还可以使用集成模型，通过多个高方差模型的融合来降低方差。

   PAC学习理论(Probably Approximately Correct)

   模型在有限的样本中，学习到真实的模型是不可能的，因此我们只要求算法可以以一定概率学习到一个近似正确的假设即可，这称之为PAC。一个PAC可学习的算法，指该算法可以在多项式时间内，从合理数量的训练集中学习到一个近似的模型。
   PAC分为两部分：

3. 近似正确：泛化错误小于一个界限

4. 可能：算法有可能以一个较大的概率学习到近似正确的假设。

   什么是表示学习？

   让机器自动的提出取有效的特征，称为特征学习，也叫表征学习。

   2.6

   有什么特征抽取的方法？

• 监督 - LDA（Linear Discriminant Analysis），抽取对一个特定的预测任务最有用的特征
• 无监督- PCA（Principal Component Analysis），自编码（Auto-Encoder）

2.7

什么是宏平均和微平均？

在有多个类别的情况下，每个类别都有自己的Precision，Recall，F1，怎么知道整体效果呢？
宏平均 - 对每个类别的P、R、F1，算均值。
微平均 - 所有样本算作一个类别，重新计算P、R、F1。受样本量大的类影响。

2.8

列举几个常见理论和定理？

• 没有免费午餐定理
• PAC学习理论
• 奥卡姆剃刀定理
• 丑小鸭定理
• 归纳偏置