似然法是在干吗?
假设一枚不均匀的硬币,出现正面的概率是一个参数,假设为,那么通过掷硬币,观察正面出现的次数,来反向推断
的取值,就是似然;而得到最可能的
的取值,就叫做极大似然估计。所以,似然法的目的就是为了找到
。
再举一个例子来看:
比如你妈经常观察到你玩游戏,那么他就会认为你玩游戏的概率大于你学习的概率,然后魔偶天他回家就见到你在玩游戏,她就会说,怎么一天就知道玩。而她的这个估计,就是利用了极大似然的原理,数学上来说,极大似然估计其实是理想地认为,对于极少的样本观测,我们很可能观测到的就是发生概率最大的那次实现。
如何找?
首先,极大似然估计是基于实验的,也就是我们先做一组实验,比如上面的掷硬币,掷硬币10次,结果正面出现6次,这是我们已知的实验结果,根据这个结果,我们可以列出一个用来表示的概率函数,也就是通过
可以计算出,我们当前这次实验结果出现的可能性大小:
%3D%5Cbinom%7B10%7D%7B6%7D%5Ctheta%5E6%20(1-%5Ctheta)%5E4#card=math&code=L%28%5Ctheta%29%3D%5Cbinom%7B10%7D%7B6%7D%5Ctheta%5E6%20%281-%5Ctheta%29%5E4&height=45&width=169),这里的
#card=math&code=L%28%5Ctheta%29&height=20&width=32)就被称之为似然函数。所以,求
的最可能的值,就转化为了求
#card=math&code=%5Cdisplaystyle%20%20%5Carg%5Cmax_%7B%5Ctheta%7D%20L%28%5Ctheta%29&height=28&width=92),
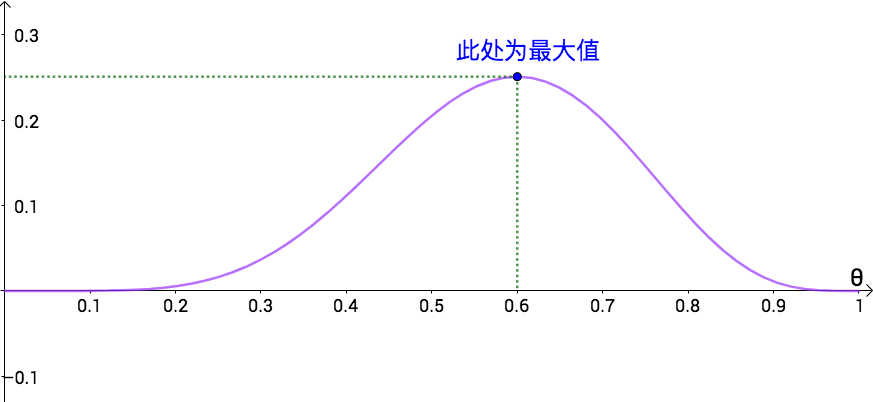
#card=math&code=L%28%5Ctheta%29&height=20&width=32)的概率分布图如下所示,我们的目的就是找到使得
#card=math&code=L%28%5Ctheta%29&height=20&width=32)极大时的
。
机器学习的用法
理解了极大似然估计,对应到机器学习上,也就是说,我们希望找到一组参数,使得训练集出现的可能性是极大的,这组参数在逻辑回归里就是特征的权重。

