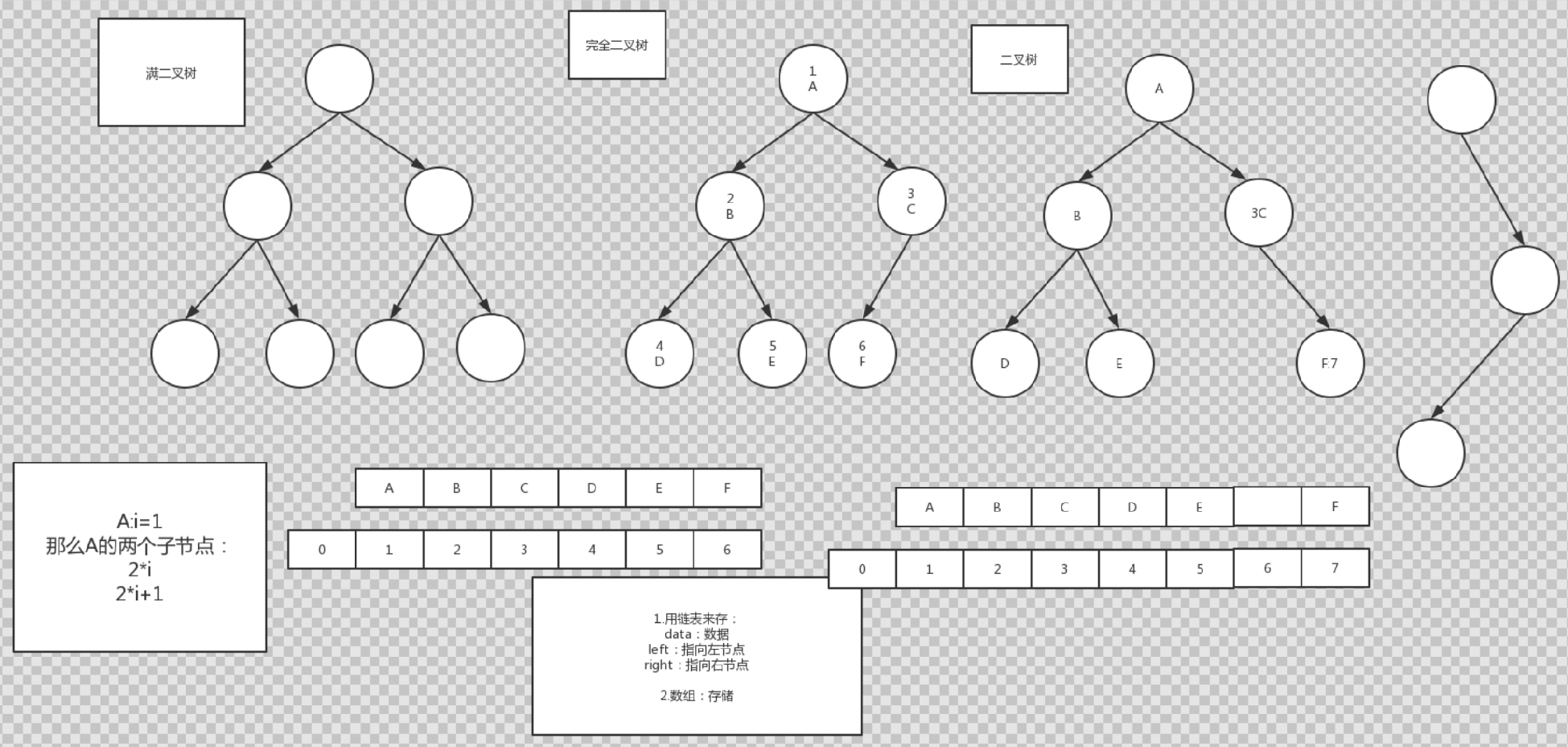
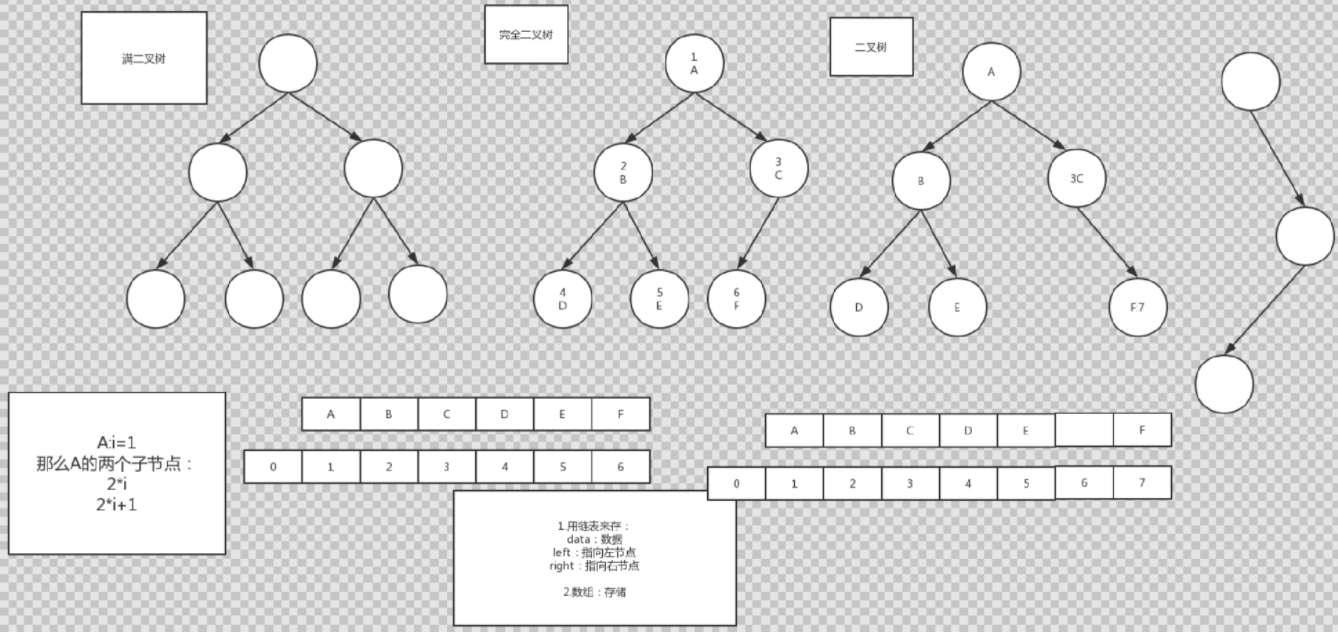
一、二叉树结构(可以用数组,链表实现)
二、二叉树术语
1.结点:树里面的元素。
2.父子关系:结点之间相连的边
3.子树:当结点大于1时,其余的结点分为的互不相交的集合称为子树
4.度:一个结点拥有的子树数量称为结点的度
5.叶子:度为0的结点
6.孩子:结点的子树的根称为孩子结点
7.双亲:和孩子结点对应
8.兄弟:同一个双亲结点
9.森林:由N个互不相交的树构成深林
10.结点的高度:结点到叶子结点的最长路径
11.结点的深度:根结点到该结点的边个数
12.结点的层数:结点的深度加1
13.树的高度:根结点的高度
三、树分类:
1.二叉树
2.二叉查找树
什么是二叉查找树:
根节点的值大于其左子树中任意一个节点的值,小于其右节点中任意一节点的值,这一规则适用于二叉查找树中的每一个节点。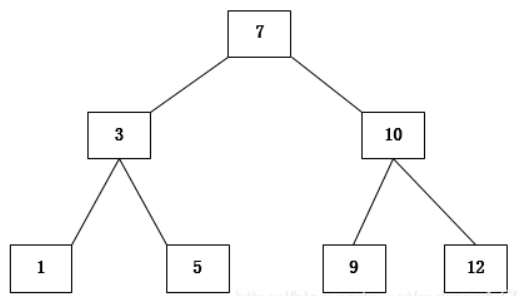
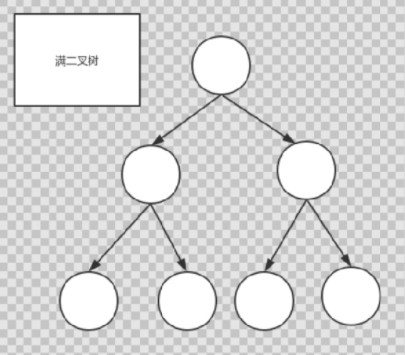
3.满二叉树
4.完全二叉树:堆排序;大顶堆,小顶堆;
完全二叉树:除最后一层外,其他的结点个数必须达到最大,并且最后一层结点都连续靠左排列。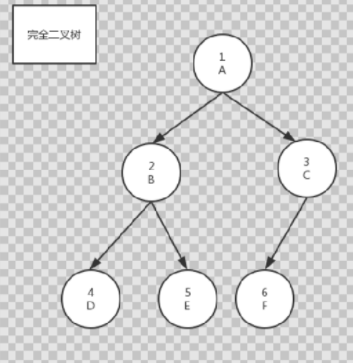
5.平衡二叉树
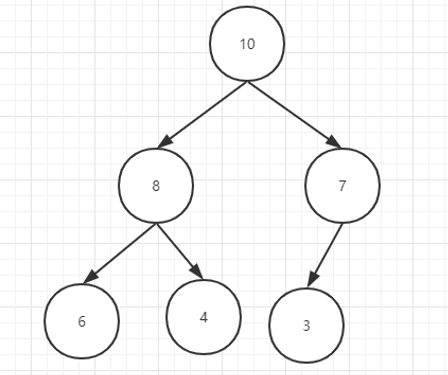
如果我的数据是一个有序的数据,那么二叉查找树就会出现下面的这种链表的情况: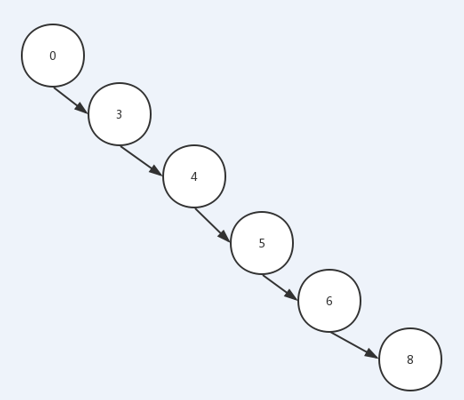
可以看出二叉树的结构就决定了其搜索的性能,那么我们应该怎么优化呢?
因此就有了AVL树和红黑树
AVL树:平衡二叉树,它的左右子树高度之差不超过1
这样确实可以避免一条直线型的结构,但还不是我们最理想的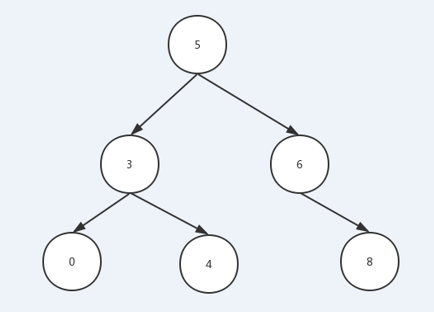
6.红黑树
红黑树,可以认为是理想状态。
由二叉树升级而来,
红黑树的性质(重点):
1.每个结点不是红色就是黑色
2.不可能有连在一起的红色结点(黑色的就可以),每个叶子节点都是黑色的空节点(NIL),也就是说,叶子节点不存储数据
3.根结点都是黑色 root
4.每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点; 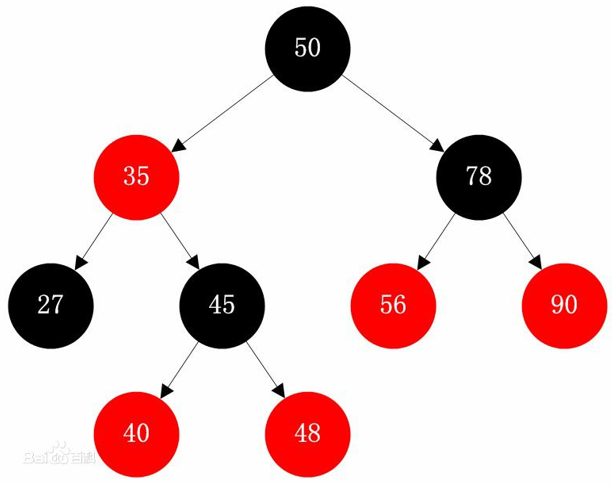
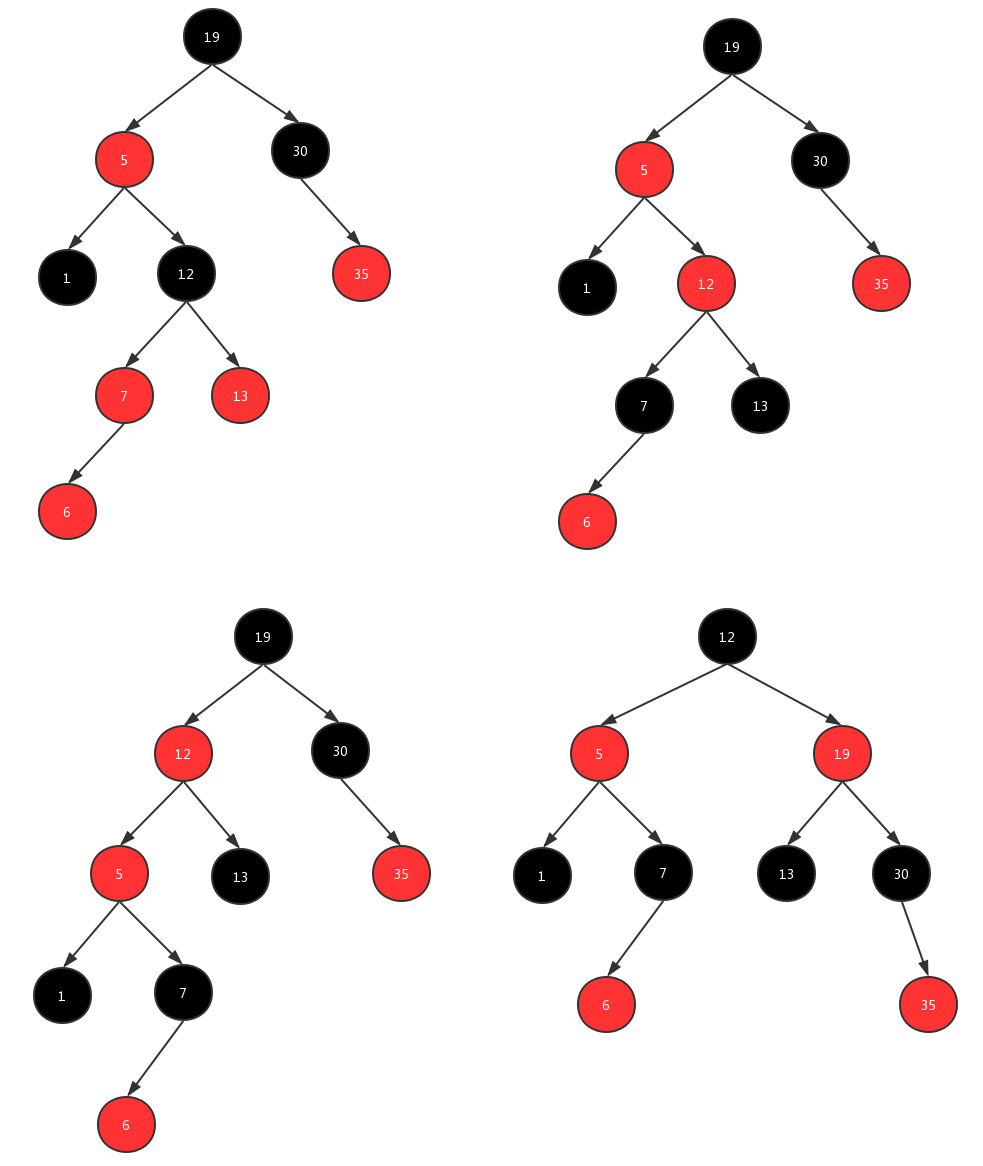
为了满足红黑树的性质,因此出现了旋转:
1.改变颜色:最简单 红变黑 黑变红
2.左旋:针对于点旋,但是点上面的子树也要跟着转。其实就是改变指针的指向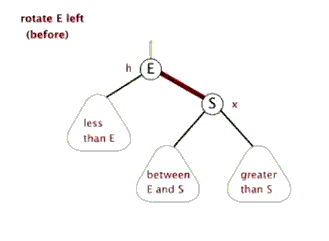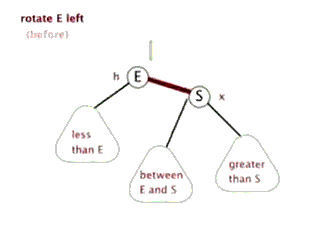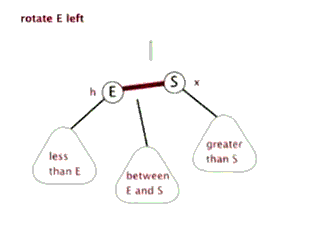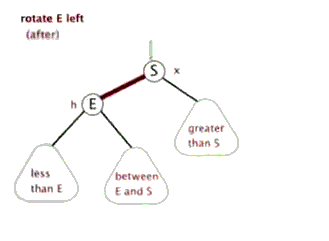
3.右旋: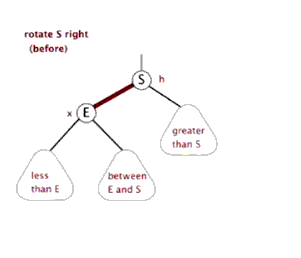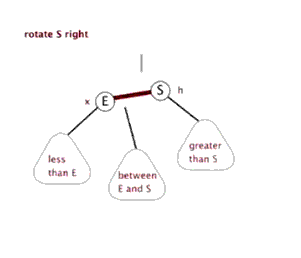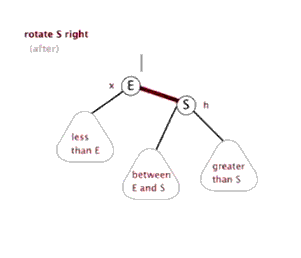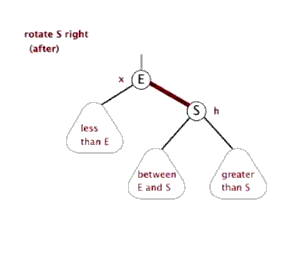
1.HashMap
2.TreeMap
3.Windows底层:查找
4.Linux进程调度,nginx等
7.B树
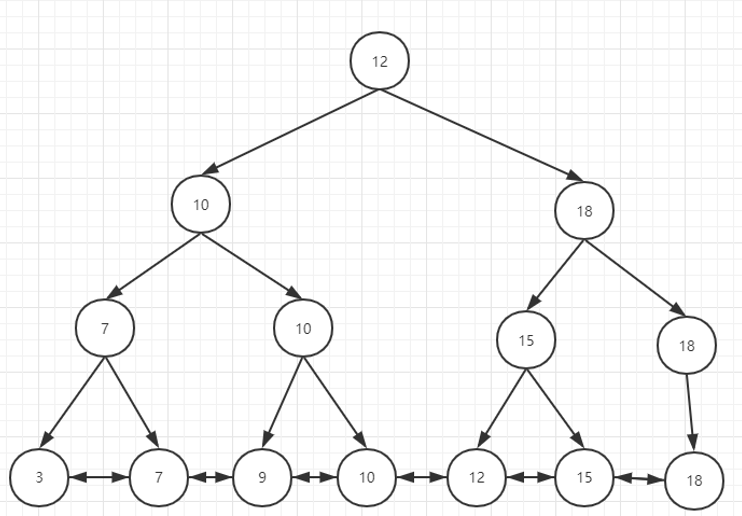
上图的B树其实是改造的二叉搜索树:
执行 select from table where id = 10
执行 select from table where id > 12
select * from table where id > 12 and id < 20
效果:
能解决我们上面所有的sql语句;
效率 logn
2^32=21亿;存储21亿个数据仅用了32层,从理论上很完美,下面分析下性能:
1.IO:指的是从磁盘读取数据。32层就要读取32次,IO的次数很多了。
2.内存,我们知道像mysql会一次把整个表的索引树加载到内存的,而非叶子节点也做数据存储的话内存会撑满溢出。
所以B树如果用来做数据器的数据存储的话还是不行的。
8.B+树
1.M阶的B+Tree:叉树
(1)每个节点最多有m个子节点
(2)除根节点外,每个节点至少有m/2个子节点,注意如果结果除不尽,就向上取整,比如5/2=3。 3/2=ceil(1.5)=2
(3)根节点要么是空,要么是独根,否则至少有2个子节点
(4)有k个子节点的节点必有k个关键码:就是 有m个数据就有m个叉叉;
(5)叶节点的高度一致:这个的 好处是什么?
满树?连续?
2.阶数:
通过上面的分析我们知道这个阶数很重要直接决定了B+Tree的查找效率以及性能,那么在Mysql中我们如何设定这阶数呢?
通过mysql的页大小决定,一般是16k。那么一个主键类型为bigint的字段建索引大约的消耗空间是多少呢?
Int:8字节,指针一个也算4字节。
一页的节点:16kb/(8b+8b)=1k 键值+指针
我们刚举例的3阶B+Tree你们计算下可以存多少索引值?
102410241024=多少?
可想而知如果在理想情况下 我们的mysql查询是不是很高效,一般最多也就4阶左右的B+Tree。
3.B-Tree和B+Tree的区别
1.B-tree所有的节点都会存数据
2.b-tree叶子节点没有链表
我们认为b-tree是b+tree的过度。
9.Trie树&赫夫曼树
给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
10.堆树
堆是什么?堆是一种特殊的树,他需要满足以下两点:
1.是一颗完全二叉树
2.其每一个节点的值都大于等于或者小于等于其左右子节点的值。
二叉搜索树:左节点小于根节点,右节点大于根节点
完全二叉树:除了最后一层,其他层每个节点都是满的且最后一层的节点都要靠左排列。