给定一个二维矩阵 matrix，以下类型的多个请求：

    • 计算其子矩形范围内元素的总和，该子矩阵的 左上角 为 (row1, col1) ，右下角 为 (row2, col2) 。

    实现 NumMatrix 类：

    • NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
    • int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素 总和 。

    示例1：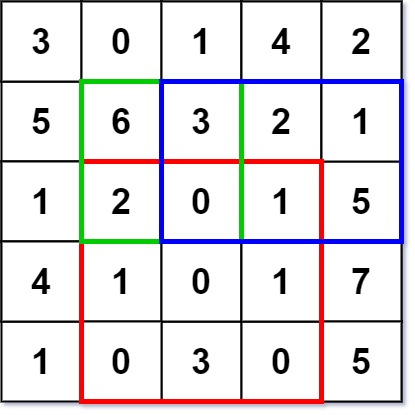
    image.png
    输入:
    [“NumMatrix”,”sumRegion”,”sumRegion”,”sumRegion”]
    [[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
    输出:
    [null, 8, 11, 12]

    解释:
    NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]);
    numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
    numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
    numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)

    常规算法：遍历求和

    1. class NumMatrix {
    3.     private int[][] matrix;
    5.     public NumMatrix(int[][] matrix) {
    6.         this.matrix = matrix;
    7.     }
    9.     public int sumRegion(int row1, int col1, int row2, int col2) {
    10.         int sum = 0;
    11.         for (int i = row1; i <= row2; i++) {
    12.             for (int j = col1; j <= col2; j++) {
    13.                 sum += matrix[i][j];
    14.             }
    15.         }
    16.         return sum;
    17.     }
    18. }

    但是此题可以看做 303. 区域和检索 - 数组不可变 的升级，同理可以考虑使用前缀和技巧

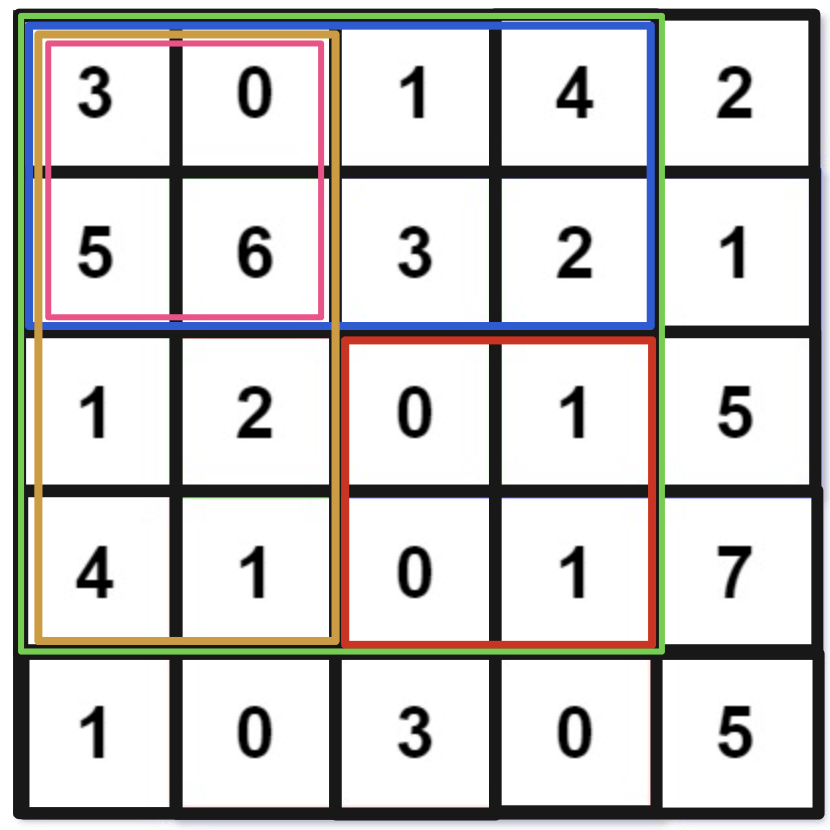
    image.png

    比如想得到红色矩阵的和，可以先分别计算绿色矩阵的和，蓝色矩阵的和，黄色矩阵的和，粉色矩阵的和，那么：
    红色矩阵的和 = 绿色矩阵的和 - 蓝色矩阵的和 - 黄色矩阵的和 + 粉色矩阵的和

    如何构建二维数组的前缀和数组呢？
    构建一维数组的前缀和数组有如下两个模板：

    1. int[] sums;
    3. public NumArray(int[] nums) {
    4.     sums = new int[nums.length + 1];
    5.     // 遍历 nums 初始化 sums
    6.     for (int i = 0; i < nums.length; i++) {
    7.         sums[i + 1] = sums[i] + nums[i];
    8.     }
    9. }
    11. public NumArray(int[] nums) {
    12.     sums = new int[nums.length + 1];
    13.     // 遍历 sums 初始化 sums
    14.     for (int i = 1; i <= sums.length; i++) {
    15.         sums[i] = sums[i - 1] + nums[i - 1];
    16.     }
    17. }

    同理构建二维数组的前缀和数组也有模板：

    1. int[][] sums;
    3. public NumMatrix(int[][] matrix) {
    4.     // 计算行数
    5.     int row = matrix.length;
    6.     // 计算列数(需判断列是否存在)
    7.     int col = row == 0 ? 0 : matrix[0].length;
    8.     sums = new int[row + 1][col + 1];
    9.     // 遍历 sums 构建 sums 
    10.     for(int i = 1; i <= row; i++) {
    11.         for (int j = 1; j <= col; j++) {
    12.             sums[i][j] = sums[i-1][j] + sums[i][j-1] - sums[i-1][j-1] + matrix[i-1][j-1];
    13.         }
    14.     }
    15. }

    利用一维数组前缀和数组求和模板：

    1. public int sumRange(int i, int j) {
    2.     return sums[j + 1] - sums[i];
    3. }

    同理利用二维数组前缀和数组求和模板：

    1. public int sumRegion(int row1, int col1, int row2, int col2) {
    2.     // 红色矩阵的和 = 绿色矩阵的和 - 蓝色矩阵的和 - 黄色矩阵的和 + 粉色矩阵的和
    3.     return sums[row2 + 1][col2 + 1] - sums[rol1][col2 + 1] - sums[rol2 + 1][col1] + sums[row1][col1];
    4. }

    完整算法：

    1. class NumMatrix {
    2.     int[][] sums;
    4.     public NumMatrix(int[][] matrix) {
    5.         // 计算行数
    6.         int row = matrix.length;
    7.         // 计算列数(需判断列是否存在)
    8.         int col = row == 0 ? 0 : matrix[0].length;
    9.         sums = new int[row + 1][col + 1];
    10.         // 遍历 sums 构建 sums
    11.         for(int i = 1; i <= row; i++) {
    12.             for (int j = 1; j <= col; j++) {
    13.                 sums[i][j] = sums[i-1][j] + sums[i][j-1] - sums[i-1][j-1] + matrix[i-1][j-1];
    14.             }
    15.         }
    16.     }
    18.     public int sumRegion(int row1, int col1, int row2, int col2) {
    19.         // 红色矩阵的和 = 绿色矩阵的和 - 蓝色矩阵的和 - 黄色矩阵的和 + 粉色矩阵的和
    20.         return sums[row2 + 1][col2 + 1] - sums[row1][col2 + 1] - sums[row2 + 1][col1] + sums[row1][col1];
    21.     }
    22. }