559. N 叉树的最大深度

给定一个 N 叉树，找到其最大深度。
最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
N 叉树输入按层序遍历序列化表示，每组子节点由空值分隔（请参见示例）。

示例 1：
输入：root = [1,null,3,2,4,null,5,6]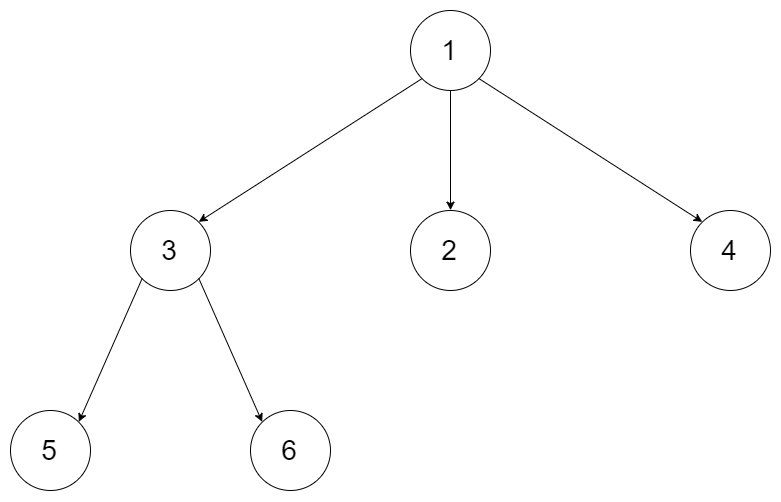

输出：3

示例 2：
输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]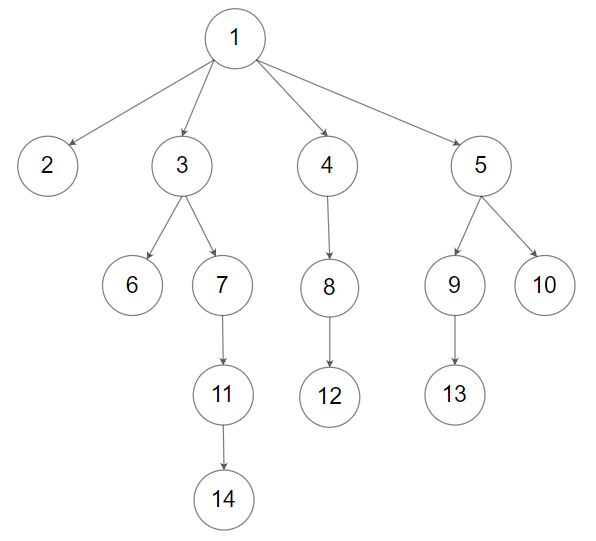

输出：5

�N 叉树的最大深度可以理解为二叉树的最大深度的一种扩展情况：104. 二叉树的最大深度

public int maxDepth(TreeNode root) {
    if(root == null) {
        return 0;
    } else {
        int leftDepth = maxDepth(root.left);
        int rightDepth = maxDepth(root.right);
        return Math.max(leftDepth, rightDepth) + 1;
    }
}

public int maxDepth(TreeNode root) {
    if(root == null) {
        return 0;
    } else {
        return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
    }
}

递归分别计算左子树的深度和右子树的深度，并且做比较，取最大值，最后树的最大深度就是最大值 + 1

那么 N 叉树递归时就是计算子树中的最大深度，然后树的最大深度就是最大值 + 1

public int maxDepth(Node root) {
    if (root == null) {
        return 0;
    } else {
        int maxChildDepth = 0;
        for (Node node : root.children) {
            maxChildDepth = Math.max(maxChildDepth, maxDepth(node));
        }
        return maxChildDepth + 1;
    }
}