106. 从中序与后序遍历序列构造二叉树

二叉树遍历：
先序遍历：对任一子树，先访问根，然后遍历其左子树，最后遍历其右子树。
中序遍历：对任一子树，先遍历其左子树，然后访问根，最后遍历其右子树。
后序遍历：对任一子树，先遍历其左子树，然后遍历其右子树，最后访问根。

二叉树遍历序列特点：
前序遍历序列：[根节点，[左子树]，[右子树]]
中序遍历序列：[[左子树]，根节点，[右子树]]
后序遍历序列：[[左子树]，[右子树]，根节点]

若要构造二叉树，只要能分别构建出根节点，根节点的左子树，根节点的右子树，那么就能完整地构造出二叉树

递归算法框架：

public TreeNode buildTree() {
    // 找到根节点的值
    int rootValue = ?;
    // 构建根节点
    TreeNode root = new TreeNode(rootValue);
    // 构建根节点的左子树
    root.left = buildTree();
    // 构建根节点的右子树
    root.right = buildTree();
    return root;
}

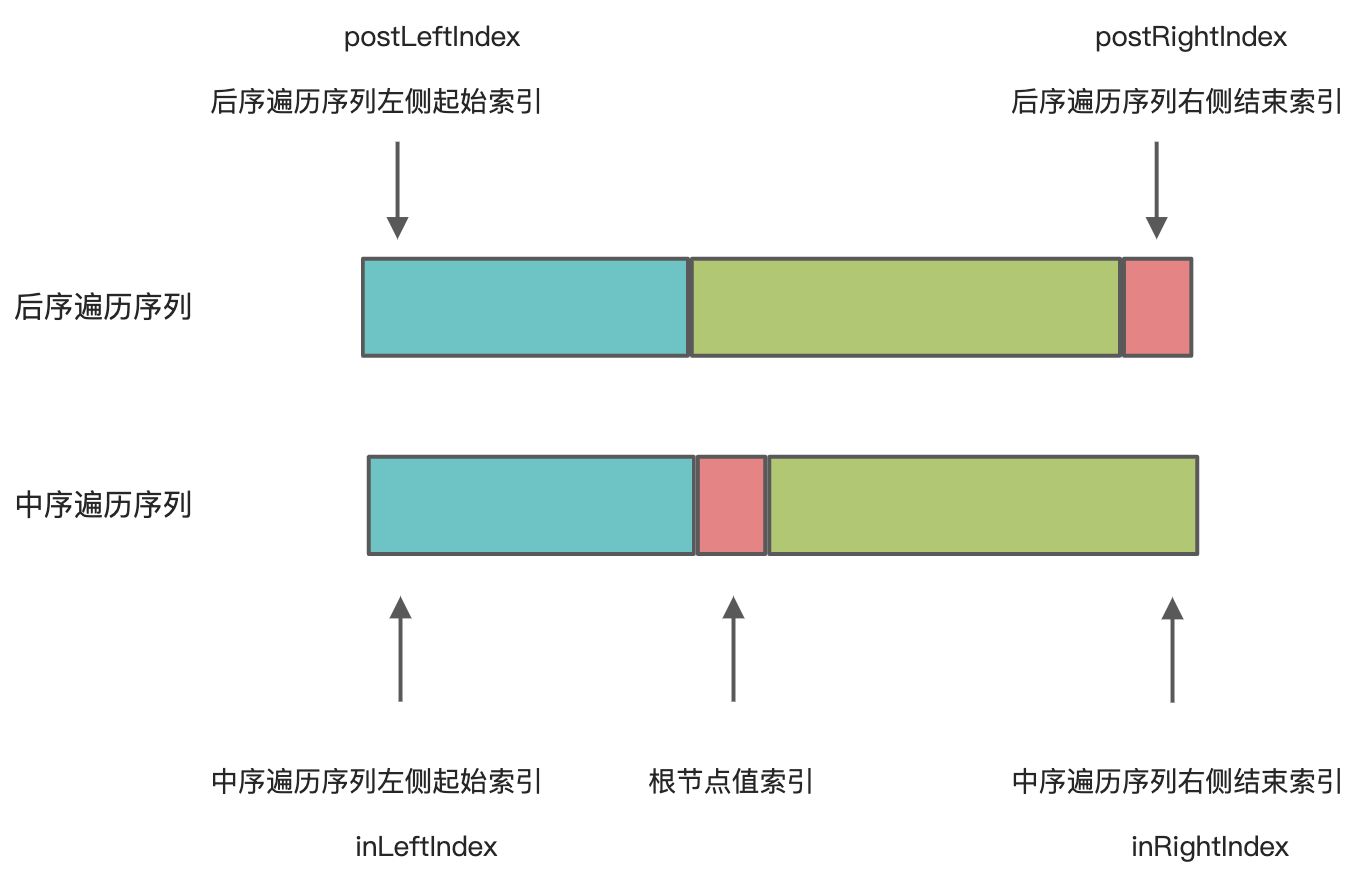
根据题意只要能确定中序遍历序列和后序遍历序列，即可最终构建出一棵二叉树
只要知道中序遍历序列左侧起始索引和中序遍历序列右侧起始索引即可确定中序遍历序列
只要知道后序遍历序列左侧起始索引和后序遍历序列右侧起始索引即可确定后序遍历序列

public TreeNode buildTree(int[] inorder, int[] postorder, 
                          int inLeftIndex, int inRightIndex, 
                          int postLeftIndex, int postRightIndex) {
    // 找到根节点的值
    int rootValue = ?;
    // 找到根节点的索引
    int rootIndex = ?;
    // 构建根节点
    TreeNode root = new TreeNode(rootValue);
    // 构建左子树
    root.left = buildTree(inorder, postorder, ?, ?, ?, ?);
    // 构建右子树
    root.right = buildTree(inorder, postorder, ?, ?, ?, ?);
    return root;
}

public TreeNode buildTree(int[] preorder, int[] inorder) {
    HashMap<Integer, Integer> valueIndexMap = new HashMap();
    for(int i = 0; i < inorder.length; i++) {
        valueIndexMap.put(inorder[i], i);
    }
    return buildTree(preorder, inorder, 
                     0, preorder.length - 1, 
                     0, inorder.length - 1, 
                     valueIndexMap);
}
public TreeNode buildTree(int[] inorder, int[] postorder,
                              int inLeftIndex, int inRightIndex,
                              int postLeftIndex, int postRightIndex,
                              HashMap<Integer, Integer> valueIndexMap) {
    if (preLeftIndex > preRightIndex) {
        return null;
    }
    // 找到根节点的值
    int rootValue = postorder[postRightIndex];
    // 找到根节点的索引
    int rootIndex = valueIndexMap.get(rootValue);
    // 左子树节点数量
    int leftSize = rootIndex - inLeftIndex;
    // 构建根节点
    TreeNode root = new TreeNode(rootValue);
    // 左子树中序遍历序列起始索引
    int leftNextInLeftIndex = inLeftIndex;
    // 左子树中序遍历序列结束索引
    int leftNextInRightIndex = inLeftIndex + leftSize - 1;
    // 左子树后序遍历序列起始索引
    int leftNextPostLeftIndex = postLeftIndex;
    // 左子树后序遍历序列结束索引
    int leftNextPostRightIndex = postLeftIndex + leftSize - 1;
    // 构建左子树
    root.left = buildTree(inorder, postorder,
            leftNextInLeftIndex, leftNextInRightIndex,
            leftNextPostLeftIndex, leftNextPostRightIndex,
            valueIndexMap);
    // 右子树中序遍历序列起始索引
    int rightNextInLeftIndex = rootIndex + 1;
    // 右子树中序遍历序列结束索引
    int rightNextInRightIndex = inRightIndex;
    // 右子树后序遍历序列起始索引
    int rightNextPostLeftIndex = postLeftIndex + leftSize;
    // 右子树后序遍历序列结束索引
    int rightNextPostRightIndex = postRightIndex - 1;
    // 构建右子树
    root.right = buildTree(inorder, postorder,
            rightNextInLeftIndex, rightNextInRightIndex,
            rightNextPostLeftIndex, rightNextPostRightIndex,
            valueIndexMap);
    return root;
}