114. 将二叉树展开为列表

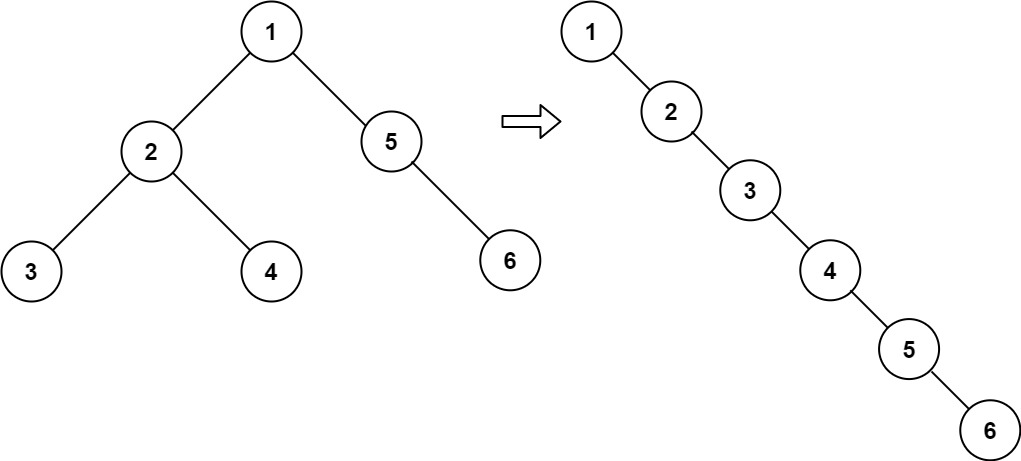
给你二叉树的根结点 root ，请你将它展开为一个单链表：

• 展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
• 展开后的单链表应该与二叉树 先序遍历 顺序相同。

分析过程

假设有一颗树

      1      
    /   \    
  2       3  
 / \     / \ 
4   5   6   7

左子树和右子树需要先变化为

   1            
 /   \         
2      5      
 \      \    
  3       6  
   \       \ 
    4       7

最后根节点进行变化

1            
 \         
  2      
   \    
    3  
     \ 
      4
       \    
        5  
         \ 
          6
           \ 
            7

根节点做了什么？

/**
 * 实现节点的拉平
 */
private void nodeNeedTodo(TreeNode node) {
    // 保存初始左子树
    TreeNode initLeft = node.left;
    // 保存初始右子树
    TreeNode initRight = node.right;
    // 移除左子树
    node.left = null;
    // 将原左子树变成右子树
    node.right = initLeft;
    // 遍历获取节点新右子树最末端的右子节点
    TreeNode temp = node;
    while (temp.right != null) {
        temp = temp.right;
    }
    // 将初始右子树变成新右子树的右子树
    temp.right = initRight;
}

先操作左子树，然后操作右子树，最后操作根节点 ，和后序遍历二叉树是很类似的

完整算法

public void flatten(TreeNode node) {
    if (node == null) {
        return;
    }
    // 先让左子树拉平
    flatten(node.left);
    // 后让右子树拉平
    flatten(node.right);
    // 最后操作根节点拉平
    nodeNeedTodo(node);
}
/**
 * 实现节点的拉平
 */
private void nodeNeedTodo(TreeNode node) {
    // 保存初始左子树
    TreeNode initLeft = node.left;
    // 保存初始右子树
    TreeNode initRight = node.right;
    // 移除左子树
    node.left = null;
    // 将原左子树变成右子树
    node.right = initLeft;
    // 遍历获取节点新右子树最末端的右子节点
    TreeNode temp = node;
    while (temp.right != null) {
        temp = temp.right;
    }
    // 将初始右子树变成新右子树的右子树
    temp.right = initRight;
}