501. 二叉搜索树中的众数

给你一个含重复值的二叉搜索树（BST）的根节点 root ，找出并返回 BST 中的所有众数（出现频率最高的元素）。
如果树中有不止一个众数，可以按 任意顺序 返回。

假定 BST 满足如下定义：

• 结点左子树中所含节点的值 小于等于 当前节点的值
• 结点右子树中所含节点的值 大于等于 当前节点的值
• 左子树和右子树都是二叉搜索树

示例 1：
输入：root = [1,null,2,2]
输出：[2]

示例 2：
输入：root = [0]
输出：[0]

众数（出现频率最高的元素），那么可以先统计值得出现频率次数

public int[] findMode(TreeNode root) {
    Map<Integer, Integer> timesMap = new HashMap<>();
    // 遍历二叉树时统计值的出现次数
    order(root, timesMap);
}
/**
 * 遍历二叉树时统计值的次数
 * @param node
 */
private void order(TreeNode node, Map<Integer, Integer> timesMap) {
    if (node == null) {
        return;
    }
    timesMap.put(node.val, timesMap.getOrDefault(node.val, 0) + 1);
    order(node.left);
    order(node.right);
}

遍历次数结果Map，得到次数最大值

public int[] findMode(TreeNode root) {
    Map<Integer, Integer> timesMap = new HashMap<>();
    // 遍历二叉树时统计值的出现次数
    order(root, timesMap);
    // 找到次数最大值
    int maxTimes = 0;
    for (Map.Entry<Integer, Integer> entry : timesMap.entrySet()) {
        maxTimes = Math.max(entry.getValue(), maxTimes);
    }
}
/**
 * 遍历二叉树时统计值的次数
 * @param node
 */
private void order(TreeNode node, Map<Integer, Integer> timesMap) {
    if (node == null) {
        return;
    }
    timesMap.put(node.val, timesMap.getOrDefault(node.val, 0) + 1);
    order(node.left);
    order(node.right);
}

再次遍历次数结果Map，找到出现最大次数的值，放入 List

public int[] findMode(TreeNode root) {
    Map<Integer, Integer> timesMap = new HashMap<>();
    // 遍历二叉树时统计值的出现次数
    order(root, timesMap);
    // 找到次数最大值
    int maxTimes = 0;
    for (Map.Entry<Integer, Integer> entry : timesMap.entrySet()) {
        maxTimes = Math.max(entry.getValue(), maxTimes);
    }
    // 找到出现次数最多的值
    List<Integer> maxTimesValList = new ArrayList<>();
    for (Map.Entry<Integer, Integer> entry : timesMap.entrySet()) {
        if (entry.getValue() == maxTimes) {
            maxTimesValList.add(entry.getKey());
        }
    }
}
/**
 * 遍历二叉树时统计值的次数
 * @param node
 */
private void order(TreeNode node, Map<Integer, Integer> timesMap) {
    if (node == null) {
        return;
    }
    timesMap.put(node.val, timesMap.getOrDefault(node.val, 0) + 1);
    order(node.left);
    order(node.right);
}

最后将 List 转为 array

public int[] findMode(TreeNode root) {
    Map<Integer, Integer> timesMap = new HashMap<>();
    // 遍历二叉树时统计值的出现次数
    order(root, timesMap);
    // 找到次数最大值
    int maxTimes = 0;
    for (Map.Entry<Integer, Integer> entry : timesMap.entrySet()) {
        maxTimes = Math.max(entry.getValue(), maxTimes);
    }
    // 找到出现次数最多的值
    List<Integer> maxTimesValList = new ArrayList<>();
    for (Map.Entry<Integer, Integer> entry : timesMap.entrySet()) {
        if (entry.getValue() == maxTimes) {
            maxTimesValList.add(entry.getKey());
        }
    }
    // List 转 array
    int[] result = new int[maxTimesValList.size()];
    for (int i = 0; i < maxTimesValList.size(); i++) {
        result[i] = maxTimesValList.get(i);
    }
    return result;
}
/**
 * 遍历二叉树时统计值的次数
 * @param node
 */
private void order(TreeNode node, Map<Integer, Integer> timesMap) {
    if (node == null) {
        return;
    }
    timesMap.put(node.val, timesMap.getOrDefault(node.val, 0) + 1);
    order(node.left);
    order(node.right);
}

优化算法，减少对 Map 的遍历次数：

int maxTimes = 0;
Map<Integer, Integer> timesMap = new HashMap<>();
public int[] findMode(TreeNode root) {
    order(root);
    // 找到出现次数最多的值
    List<Integer> maxTimesValList = new ArrayList<>();
    for (Map.Entry<Integer, Integer> entry : timesMap.entrySet()) {
        if (entry.getValue() == maxTimes) {
            maxTimesValList.add(entry.getKey());
        }
    }
    // List 转 array
    int[] result = new int[maxTimesValList.size()];
    for (int i = 0; i < maxTimesValList.size(); i++) {
        result[i] = maxTimesValList.get(i);
    }
    return result;
}
/**
 * 遍历二叉树时统计值的次数
 * @param node
 */
private void order(TreeNode node) {
    if (node == null) {
        return;
    }
    int times = timesMap.getOrDefault(node.val, 0).intValue() + 1;
    maxTimes = Math.max(maxTimes, times);
    timesMap.put(node.val, times);
    order(node.left);
    order(node.right);
}

上述算法可以找出并返回二叉树（自然也支持二叉搜索树）中的所有众数。

但是题目中既然提到了二叉搜索树，那么二叉搜索树和普通二叉树有什么区别呢？

二叉搜索树的特点：

• 左子树的值都比根节点的值小
• 右子树的值都比根节点的值大

正因为二叉搜索树的特点，那么如果中序遍历二叉搜索树，其遍历结果将是一个有序数组！！！

public int[] findMode(TreeNode root) {
    List<Integer> valList = new ArrayList<>();
    inOrder(root, valList);
}
/**
 * 中序遍历二叉搜索树，得到升序的遍历结果
 * @param node
 */
private void inOrder(TreeNode node, List<Integer> valList) {
    if (node == null) {
        return;
    }
    inOrder(node.left, valList);
    valList.add(node.val);
    inOrder(node.right, valList);
}

那怎么从一个升序的有序数组中获取到众数集合呢？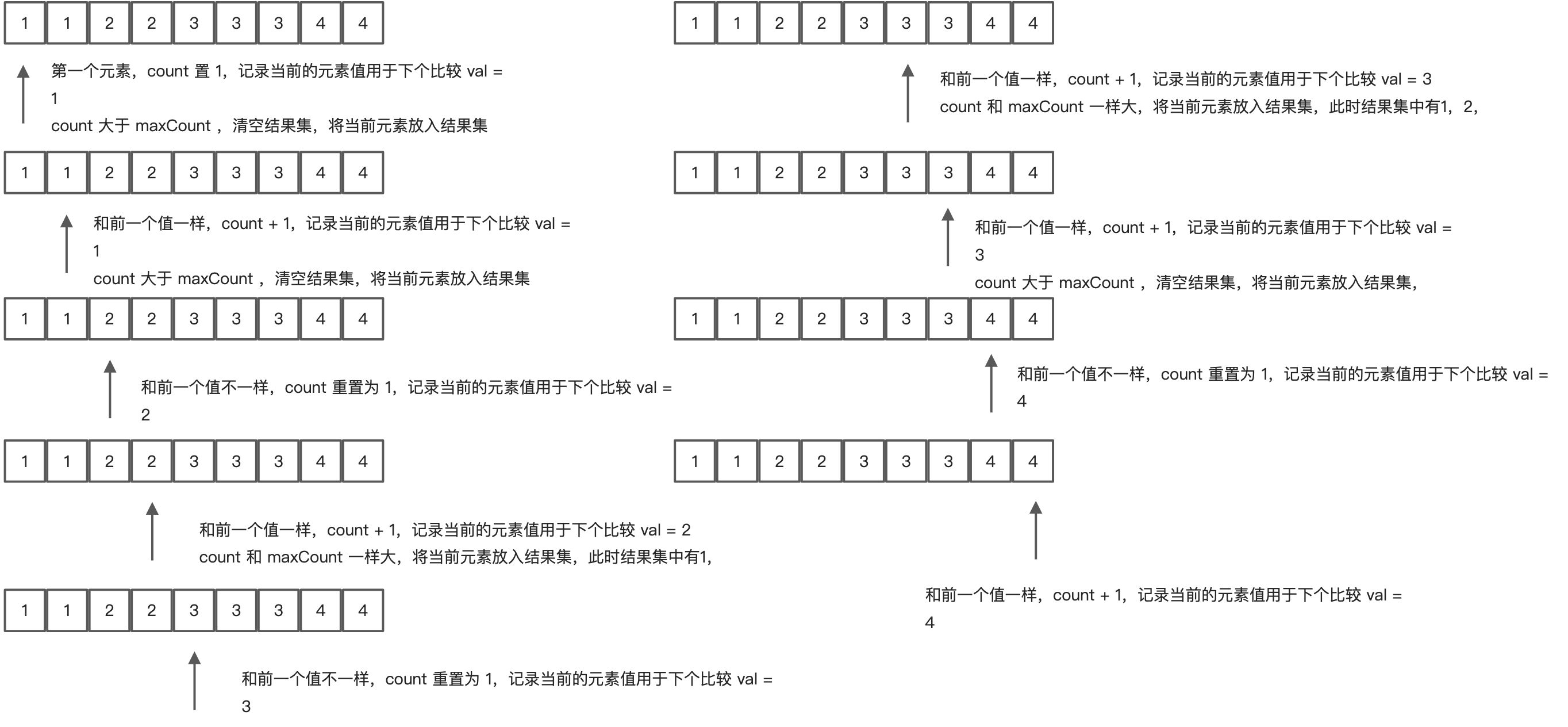

List<Integer> maxValList = new ArrayList<>();
int maxCount = 0;
int preVal = -1;
int count = 0;
for (Integer val : valList) {
    if (preVal == -1) {
        // 初始化为1
        count = 1;
    } else if (preVal == val) {
        // 值相等，次数加1
        count++;
    } else {
        // 值不相等，次数重置为1
        count = 1;
    }
    // 记录当前值用于下一次比较
    preVal = val;
    if (count == maxCount) {
        // 若次数等于最大次数，将当前值放入结果集
        maxValList.add(val);
    }
    if (count > maxCount) {
        // 若次数大于最大次数，清空结果集
        maxValList.clear();
        // 将当前值放入结果集
        maxValList.add(val);
        // 将当前次数作为新的最大次数
        maxCount = count;
    }
}

完整地算法：

public int[] findMode(TreeNode root) {
    List<Integer> valList = new ArrayList<>();
    inOrder(root, valList);
    List<Integer> maxValList = new ArrayList<>();
    int maxCount = 0;
    int preVal = -1;
    int count = 0;
    for (Integer val : valList) {
        if (preVal == -1) {
            // 初始化为1
            count = 1;
        } else if (preVal == val) {
            // 值相等，次数加1
            count++;
        } else {
            // 值不相等，次数重置为1
            count = 1;
        }
        // 记录当前值用于下一次比较
        preVal = val;
        if (count == maxCount) {
            // 若次数等于最大次数，将当前值放入结果集
            maxValList.add(val);
        }
        if (count > maxCount) {
            // 若次数大于最大次数，清空结果集
            maxValList.clear();
            // 将当前值放入结果集
            maxValList.add(val);
            // 将当前次数作为新的最大次数
            maxCount = count;
        }
    }
    // List 转 array
    int[] result = new int[maxValList.size()];
    for (int i = 0; i < maxValList.size(); i++) {
        result[i] = maxValList.get(i);
    }
    return result;
}
private void inOrder(TreeNode node, List<Integer> valList) {
    if (node == null) {
        return;
    }
    inOrder(node.left, valList);
    valList.add(node.val);
    inOrder(node.right, valList);
}

优化算法：

 public int[] findMode(TreeNode root) {
    List<Integer> maxValList = new ArrayList<>();
    inOrder(root, maxValList);
    // List 转 array
    int[] result = new int[maxValList.size()];
    for (int i = 0; i < maxValList.size(); i++) {
        result[i] = maxValList.get(i);
    }
    return result;
}
/**
 * 中序遍历二叉搜索树，得到升序的遍历结果
 * @param node
 */
TreeNode pre = null;
int count;
int maxCount = 0;
public void inOrder(TreeNode node, List<Integer> maxValList) {
    if (node == null) {
        return;
    }
    inOrder(node.left, maxValList);
    if (pre == null) {
        // 第一个节点
        count = 1;
    } else if (node.val == pre.val) {
        // 当前节点和上一个节点值相等
        count++;
    } else {
        // 当前节点和上一个节点值不相等
        count = 1;
    }
    // 记录当前值
    pre = node;
    // 当前值出现次数和最大次数相等
    if (count == maxCount) {
        // 放入当前值到目标集合
        maxValList.add(node.val);
    }
    if (count > maxCount) {
        // 出现新的最大次数
        // 清空集合
        maxValList.clear();
        // 放入当前值到目标集合
        maxValList.add(node.val);
        // 重置最大次数
        maxCount = count;
    }
    inOrder(node.right, maxValList);
}