取向分布函数（orientation distribution function，ODF）是表示晶体（或样品）要素三维空间分布的一种择优取向的表示形式。晶体的取向用bunge-Euler角（7.2 取向（差）分布函数 - 图1，7.2 取向（差）分布函数 - 图2，7.2 取向（差）分布函数 - 图3）表示，并由此建立一个以7.2 取向（差）分布函数 - 图4，7.2 取向（差）分布函数 - 图5，7.2 取向（差）分布函数 - 图6为轴的直角坐标系，称为Euler空间。如果将试样中所有晶粒的取向都标绘在Euler空间，则可得到所测试样的三维取向分布，即用取向分布函数表示试样的织构。此外，由于取向差可以表达为角轴对，根据晶体对称性，角轴对中总可以找到一个旋转角度最小及所对应的旋转轴（也称disorientation），因因而角轴对就可以在三维空间构成一个取向差空间，因而可以描述EBSD扫描区域任意两点之间的取向差（非相关取向差）的空间分布规律，即取向差分布函数（misorientation distribution function, MDF）。在EBSDTool里，用户在主界面点击“Texture”->“ODF & MDF Analysis”或直接点击odf&mdf.png，可以打开图7-3左侧所示的界面。
    对于ODF，提供了8种不同的表示形式，列表中显示默认为“phi2”：

    1. Rodrigues–Frank space：罗德里格斯-弗兰克空间；对于给定一个欧拉角，可以将其转为罗德里格斯矢量，矢量的坐标范围最终可以构成一个空间封闭体积。对于m-3m劳厄群的晶体，如果不考虑样品对称性（Specimen Symmetry 选项为Triclinic），其空间形状为截角立方体；如果考虑样品对称性为Orthorhombic，即正交对称，则空间形状为截角立方体的四分之一。
    2. 3D：以7.2 取向（差）分布函数 - 图8，7.2 取向（差）分布函数 - 图9，7.2 取向（差）分布函数 - 图10为坐标轴所构成的三维空间区域，即取向空间，不同劳厄群对应的三个欧拉角范围不同（表6-1所示），其中7.2 取向（差）分布函数 - 图11没有范围限制，其主要与样品对称性有关，样品对称性为Triclinic，则7.2 取向（差）分布函数 - 图12范围0~360度；如果样品对称性为Orthorhombic，则7.2 取向（差）分布函数 - 图13范围0~90度。
    3. Axis/Angle Projection：角轴对的投影
    4. phi1 section：垂直7.2 取向（差）分布函数 - 图14轴对取向空间进行切片，可以设置切片数量“Section Number”，，也可以定义在某个7.2 取向（差）分布函数 - 图15值处（“Individual Section (deg)”）进行切片
    5. Phi section：垂直7.2 取向（差）分布函数 - 图16轴对取向空间进行切片，可以设置切片数量“Section Number”，也可以定义在某个7.2 取向（差）分布函数 - 图17值处（“Individual Section (deg)”）进行切片
    6. phi2 section：垂直7.2 取向（差）分布函数 - 图18轴对取向空间进行切片，可以设置切片数量“Section Number”，也可以定义在某个7.2 取向（差）分布函数 - 图19值处（“Individual Section (deg)”）进行切片。如图7-3右侧显示。这种表达方式是最常见的，也是大多数论文中所使用的。
    7. gamma section：Matthies 欧拉角
    8. sigma：7.2 取向（差）分布函数 - 图20分布

    对于MDF，列表中只有两种表达方式，一种是Rodrigues–Frank space，将MDF表达在取向差Rodrigues–Frank空间中；另一种是将取向差角切片，然后将对应的旋转轴表达在反极图中。
    其他的显示设置选项，与7.1节界面类似，不再详细介绍。
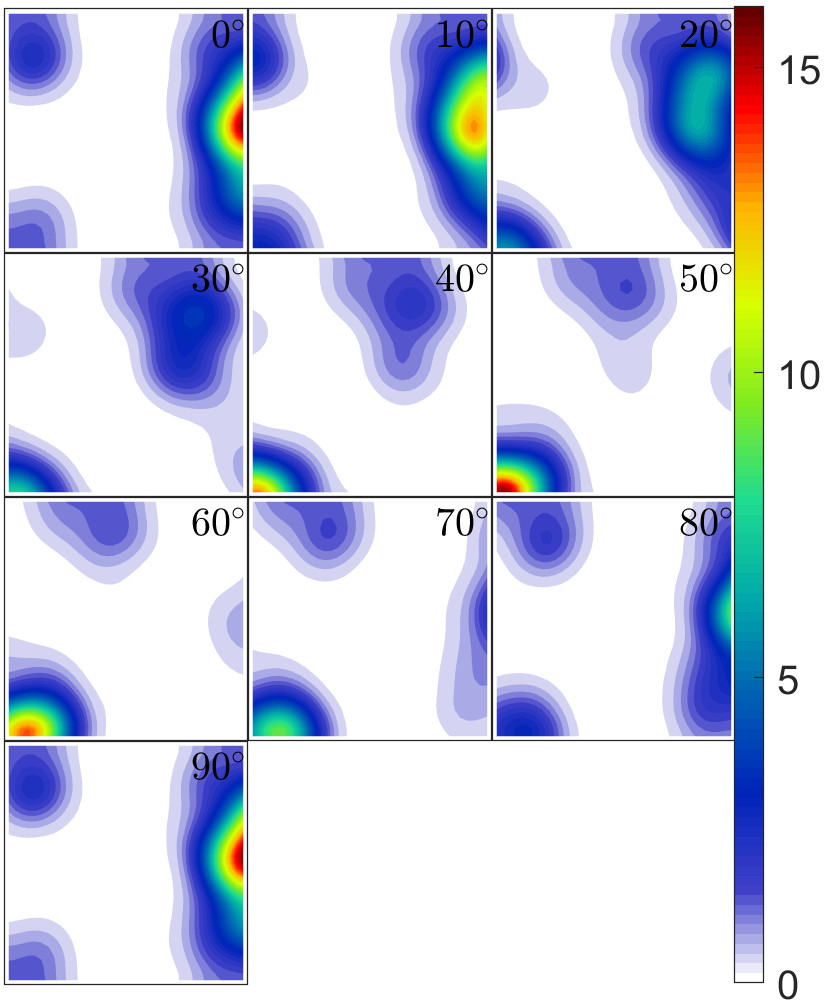
    image.pngimage.png
    图7-3 取向（差）分布函数界面