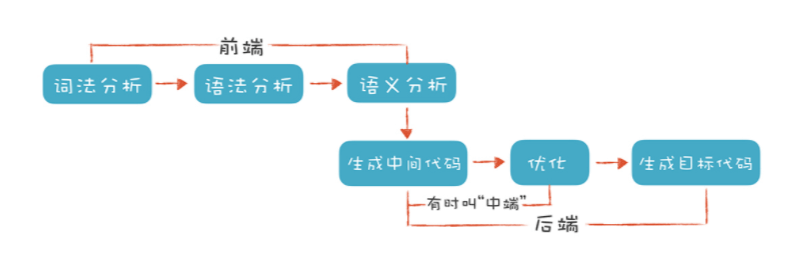
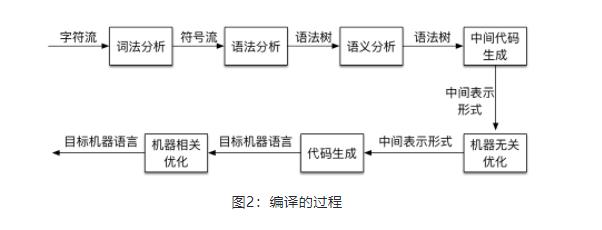
词法分析
Lexical Analysis takes the raw code and splits it apart into these things called tokens by a thing called a tokenizer (or lexer). Tokens are an array of tiny little objects that describe an isolated piece of the syntax. They could be numbers, labels, punctuation, operators, whatever.
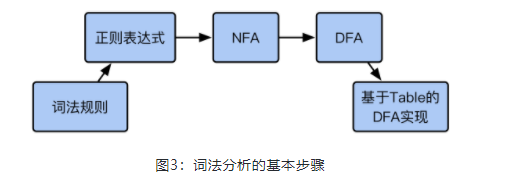
- 通过从左往右阅读源码将字符解析为一个个词法单位(token)
- 利用向前看(lookahead)操作来确定当前的词素是否结束以及下一个词素是否开始
有限自动机
依据构造好的有限自动机,在不同的状态中迁移,从而解析出 Token 来
正则表达式
常用的词法都用正则表达式描述出来的

//Tokens might look something like this:[{ type: 'paren', value: '(' },{ type: 'name', value: 'add' },{ type: 'number', value: '2' },{ type: 'paren', value: '(' },{ type: 'name', value: 'subtract' },{ type: 'number', value: '4' },{ type: 'number', value: '2' },{ type: 'paren', value: ')' },{ type: 'paren', value: ')' },]
看了这里的转换才知道那些 XXX括号的算法题是干嘛用的了
// We start by accepting an input string of code, and we're gonna set up two// things...function tokenizer(input) {// A `current` variable for tracking our position in the code like a cursor.let current = 0;// And a `tokens` array for pushing our tokens to.let tokens = [];// We start by creating a `while` loop where we are setting up our `current`// variable to be incremented as much as we want `inside` the loop.//// We do this because we may want to increment `current` many times within a// single loop because our tokens can be any length.while (current < input.length) {// We're also going to store the `current` character in the `input`.let char = input[current];// The first thing we want to check for is an open parenthesis. This will// later be used for `CallExpression` but for now we only care about the// character.//// We check to see if we have an open parenthesis:if (char === '(') {// If we do, we push a new token with the type `paren` and set the value// to an open parenthesis.tokens.push({type: 'paren',value: '(',});// Then we increment `current`current++;// And we `continue` onto the next cycle of the loop.continue;}// Next we're going to check for a closing parenthesis. We do the same exact// thing as before: Check for a closing parenthesis, add a new token,// increment `current`, and `continue`.if (char === ')') {tokens.push({type: 'paren',value: ')',});current++;continue;}// Moving on, we're now going to check for whitespace. This is interesting// because we care that whitespace exists to separate characters, but it// isn't actually important for us to store as a token. We would only throw// it out later.//// So here we're just going to test for existence and if it does exist we're// going to just `continue` on.let WHITESPACE = /\s/;if (WHITESPACE.test(char)) {current++;continue;}// The next type of token is a number. This is different than what we have// seen before because a number could be any number of characters and we// want to capture the entire sequence of characters as one token.//// (add 123 456)// ^^^ ^^^// Only two separate tokens//// So we start this off when we encounter the first number in a sequence.let NUMBERS = /[0-9]/;if (NUMBERS.test(char)) {// We're going to create a `value` string that we are going to push// characters to.let value = '';// Then we're going to loop through each character in the sequence until// we encounter a character that is not a number, pushing each character// that is a number to our `value` and incrementing `current` as we go.while (NUMBERS.test(char)) {value += char;char = input[++current];}// After that we push our `number` token to the `tokens` array.tokens.push({ type: 'number', value });// And we continue on.continue;}// We'll also add support for strings in our language which will be any// text surrounded by double quotes (").//// (concat "foo" "bar")// ^^^ ^^^ string tokens//// We'll start by checking for the opening quote:if (char === '"') {// Keep a `value` variable for building up our string token.let value = '';// We'll skip the opening double quote in our token.char = input[++current];// Then we'll iterate through each character until we reach another// double quote.while (char !== '"') {value += char;char = input[++current];}// Skip the closing double quote.char = input[++current];// And add our `string` token to the `tokens` array.tokens.push({ type: 'string', value });continue;}// The last type of token will be a `name` token. This is a sequence of// letters instead of numbers, that are the names of functions in our lisp// syntax.//// (add 2 4)// ^^^// Name token//let LETTERS = /[a-z]/i;if (LETTERS.test(char)) {let value = '';// Again we're just going to loop through all the letters pushing them to// a value.while (LETTERS.test(char)) {value += char;char = input[++current];}// And pushing that value as a token with the type `name` and continuing.tokens.push({ type: 'name', value });continue;}// Finally if we have not matched a character by now, we're going to throw// an error and completely exit.throw new TypeError('I dont know what this character is: ' + char);}// Then at the end of our `tokenizer` we simply return the tokens array.return tokens;}
语法分析
在这里将词法分析之后的 token 转换为 AST 树,在这里就看出递归算法、回溯算法的作用了,手动狗头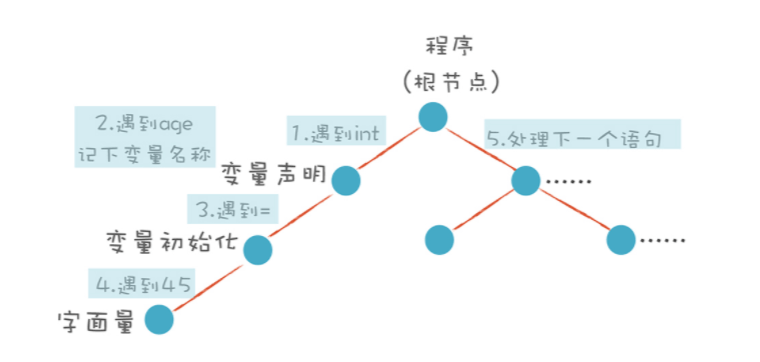
// And an Abstract Syntax Tree (AST) might look like this:{type: 'Program',body: [{type: 'CallExpression',name: 'add',params: [{type: 'NumberLiteral',value: '2',}, {type: 'CallExpression',name: 'subtract',params: [{type: 'NumberLiteral',value: '4',}, {type: 'NumberLiteral',value: '2',}]}]}]}
// Okay, so we define a `parser` function that accepts our array of `tokens`.function parser(tokens) {// Again we keep a `current` variable that we will use as a cursor.let current = 0;// But this time we're going to use recursion instead of a `while` loop. So we// define a `walk` function.function walk() {// Inside the walk function we start by grabbing the `current` token.let token = tokens[current];// We're going to split each type of token off into a different code path,// starting off with `number` tokens.//// We test to see if we have a `number` token.if (token.type === 'number') {// If we have one, we'll increment `current`.current++;// And we'll return a new AST node called `NumberLiteral` and setting its// value to the value of our token.return {type: 'NumberLiteral',value: token.value,};}// If we have a string we will do the same as number and create a// `StringLiteral` node.if (token.type === 'string') {current++;return {type: 'StringLiteral',value: token.value,};}// Next we're going to look for CallExpressions. We start this off when we// encounter an open parenthesis.if (token.type === 'paren' &&token.value === '(') {// We'll increment `current` to skip the parenthesis since we don't care// about it in our AST.token = tokens[++current];// We create a base node with the type `CallExpression`, and we're going// to set the name as the current token's value since the next token after// the open parenthesis is the name of the function.let node = {type: 'CallExpression',name: token.value,params: [],};// We increment `current` *again* to skip the name token.token = tokens[++current];while ((token.type !== 'paren') ||(token.type === 'paren' && token.value !== ')')) {// we'll call the `walk` function which will return a `node` and we'll// push it into our `node.params`.node.params.push(walk());token = tokens[current];}// Finally we will increment `current` one last time to skip the closing// parenthesis.current++;// And return the node.return node;}// Again, if we haven't recognized the token type by now we're going to// throw an error.throw new TypeError(token.type);}// Now, we're going to create our AST which will have a root which is a// `Program` node.let ast = {type: 'Program',body: [],};while (current < tokens.length) {ast.body.push(walk());}// At the end of our parser we'll return the AST.return ast;}

