image.png

  1. @inproceedings{park2019relational,
  2.   title={Relational Knowledge Distillation},
  3.   author={Park, Wonpyo and Kim, Dongju and Lu, Yan and Cho, Minsu},
  4.   booktitle={Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition},
  5.   pages={3967--3976},
  6.   year={2019}
  7. }

主要工作

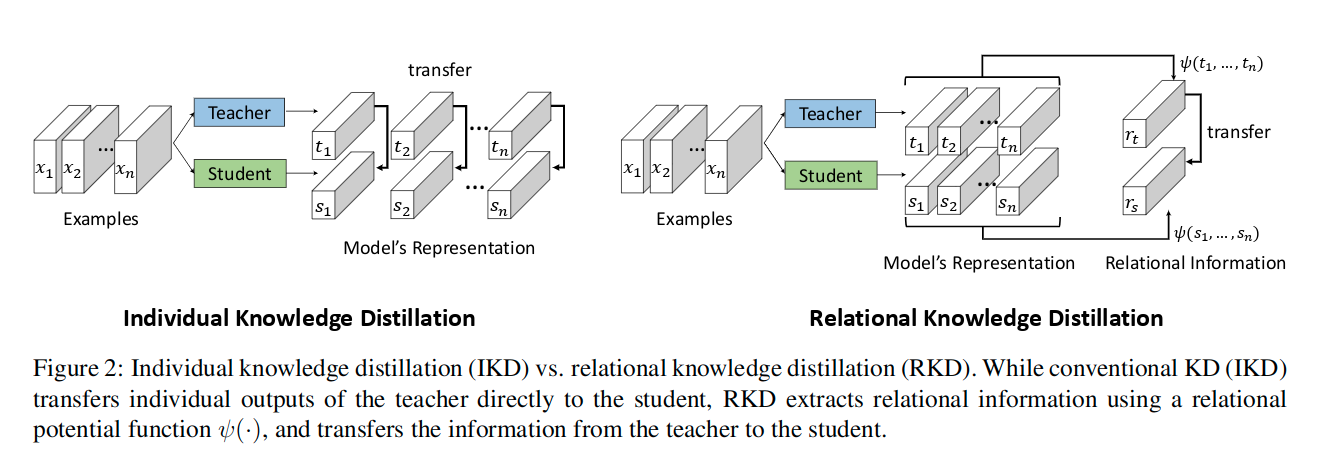
这里表示的是通过对于输入的样本之间的关系进行挖掘，进而获取更多的具有不变性的高阶信息。

我们工作的核心原则是，学习到的数据的表征关系比单独的信息能更好地呈现知识的构成，单个数据示例（例如，图像）能获得与表征系统中的其他数据示例相关或相反的含义，因此主要信息位于数据嵌入空间的结构中。

主要结构

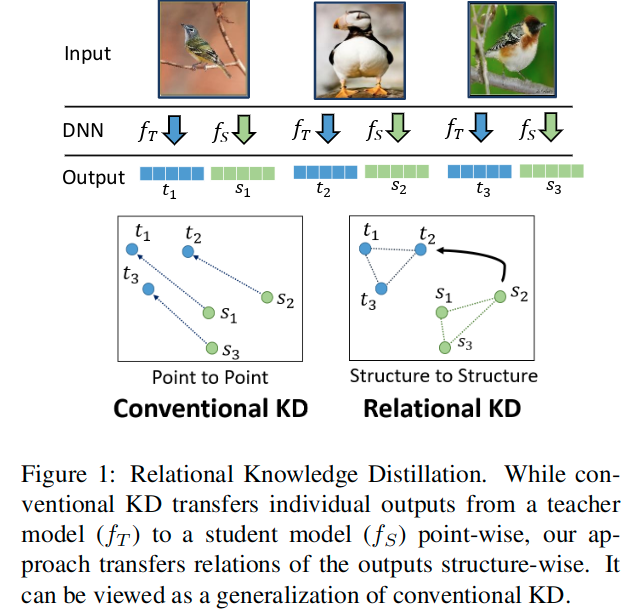
image.png

image.png

损失函数

这里提出了两种蒸馏损失函数，一种是使用batch中的两个样本的输出计算的距离损失，另一个使用三个样本计算的角度损失。这里的(CVPR 2019) Relational Knowledge Distillation - 图4表示包含n个样本的数据元组。

In sampling tuples of examples for the proposed distillation losses, we simply use all possible tuples (i.e., pairs or triplets) from examples in a given mini-batch.

For RKD, the distillation target function f can be chosen as output of any layer of teacher/student networks in principle. However, since the distance/angle-wise losses do not transfer individual outputs of the teacher, it is not adequate to use them alone to where the individual output values themselves are crucial, e.g., softmax layer for classification. In that case, it needs to be used together with IKD losses or task-specific losses. In most of the other cases, RKD is applicable and effective in our experience.

这里用到了Huber Loss（smooth l1 loss）：

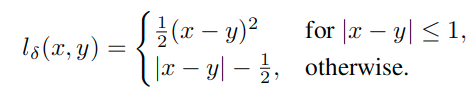
image.png

下面的式子中的范数表示的都是L2范数。因为内部都是矢量。

Distance-wise distillation loss

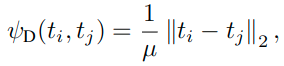
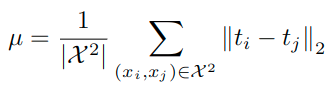
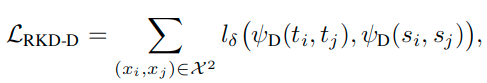
image.png
image.png
image.png

Angle-wise distillation loss

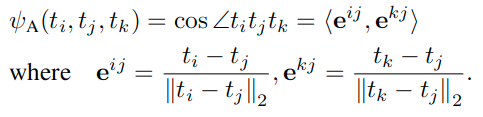
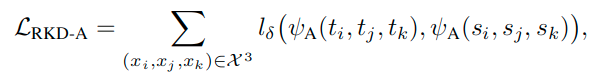
image.png
image.png

这里实际上在在训练过程中，多个蒸馏损失函数，包括提出的RKD损失，可以单独使用，也可以与特定任务的损失函数(如交叉熵)一起使用。

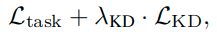
image.png

  1. class RKdAngle(nn.Module):
  2.     def forward(self, student, teacher):
  3.         # 输入 student, teacher：N x C
  5.         with torch.no_grad():
  6.             # 使用广播机制实现了各个样本（任意的一个i和任意的一个j）间的差值的计算
  7.             td = (teacher.unsqueeze(0) - teacher.unsqueeze(1))  # N x N x C
  8.             # 沿着dim=2维度除以p范数进行归一化，也就是对通道归一化
  9.             norm_td = F.normalize(td, p=2, dim=2)  # N x N x C
  10.             # 计算夹角
  11.             t_angle = torch.bmm(norm_td, norm_td.transpose(1, 2)).view(-1)
  13.         sd = (student.unsqueeze(0) - student.unsqueeze(1))
  14.         norm_sd = F.normalize(sd, p=2, dim=2)
  15.         s_angle = torch.bmm(norm_sd, norm_sd.transpose(1, 2)).view(-1)
  17.         loss = F.smooth_l1_loss(s_angle, t_angle, reduction='elementwise_mean')
  18.         return loss
  20. def pdist(e, squared=False, eps=1e-12):
  21.     # e：N x C
  22.     # 计算成对距离，也就是计算e中的N个C为矢量之间任意一对儿的欧式距离，这里使用矩阵乘法实现
  23.     e_square = e.pow(2).sum(dim=1)  # N x 1
  24.     prod = e @ e.t()  # N x N，这部分计算的是`(A-B)^2`展开式中的`AB`的结果
  25.     # 计算了`(A-B)^2`，即成对距离
  26.     res = (e_square.unsqueeze(1) + e_square.unsqueeze(0) - 2 * prod).clamp(min=eps)
  28.     if not squared:
  29.         res = res.sqrt()
  31.     res = res.clone()
  32.     res[range(len(e)), range(len(e))] = 0
  33.     return res
  36. class RkdDistance(nn.Module):
  37.     def forward(self, student, teacher):
  38.         with torch.no_grad():
  39.             # 计算了任意一对儿样本输出对应的距离
  40.             t_d = pdist(teacher, squared=False)
  41.             # 只针对非零距离进行计算
  42.             mean_td = t_d[t_d>0].mean()
  43.             t_d = t_d / mean_td
  45.         d = pdist(student, squared=False)
  46.         mean_d = d[d>0].mean()
  47.         d = d / mean_d
  49.         loss = F.smooth_l1_loss(d, t_d, reduction='elementwise_mean')
  50.         return loss

个人想法

19年ICCV的文章Similarity-Preserving Knowledge Distillation和该文想法很相似，都是考虑的batch内样本之间的相似性。

Similarity-Preserving Knowledge Distillation · 语雀

相关链接