这篇文章则主要通过卷积的group操作以及在训练时候的剪枝来达到降低显存提高速度的目的。
作者的实验证明,CondenseNet可以在只需要DenseNet的1/10训练时间的前提下,达到和DenseNet差不多的准确率。
总结下这篇文章的几个特点:
- 引入组卷积操作,而且在1*1卷积中引入可学习组操作时做了改进。
- 训练一开始就对权重做剪枝,而不是对训练好的模型做剪枝。
- 在DenseNet基础上引入跨block的密集连接。
动机
为了在计算资源有限的设备上使用现有的CNN网络, 来实现一些类似于机器人/自动驾驶或者移动设备上的实时推理的应用, 现在人们已经开发尝试了很多的方法, 包括剪除冗余连接, 使用低准确率或者量化后的权重, 或者使用更为有效的网络结构.
对于在移动设备上应用深度学习, 一个好的结构应该是允许在训练期间可以快速的并行计算, 而测试时它可以很紧凑, 使用更少的资源.
最近的工作 [4,20] 表明 CNNs 有很多冗余。逐层连接模式强制网络从整个网络的早期层复制特征。DenseNet 架构 [19] 通过直接将每个层与之前的所有层连接起来,从而减轻了对特征复制的需求,从而导致特征重用。虽然效率更高,但我们仍然可以假设,当后期不需要某些早期特征时,密集连接会引入冗余。
贡献
提出了一种新的方法来修剪层之间的冗余连接,然后引入一个更有效的架构。与以前的修剪方法相比,提出的方法在训练过程中自动学习稀疏网络,并产生一个常规的连接模式,可以有效地使用组卷积实现。具体来说,我们将一个层的过滤器分成多个组,并在训练过程中逐步删除每个组不太重要的特征的连接。重要的是,传入特征的组不是预定义的,而是学习的。由此产生的模型,称为CondenseNet,可以有效地在GPU上训练,并在移动设备上具有较高的推理速度。
剪枝与分组卷积
CondenseNet也依赖剪枝技术,但在两个主要的方式上, 不同于以前的方法:
- 权重剪枝是在训练的早期阶段开始, 这比整个使用 L1 正则化更有效和有效。
- CondenseNet具有比滤波器级别剪枝更高的稀疏度,可以产生高效的组卷积-达到稀疏性和规律性之间的平衡(sweet spot)。
CondenseNet依赖于深度上的分组卷积, 但是相比于MobileNet, ShuffleNet, NASNet等所使用的深度可分离卷积, 计算更高效.
(个人理解, 可以简单计算一下, 对于输入的特征图 NxCxHxW, 要获得输出NxCxHxW, 若使用深度可分离卷积, 假定逐通道卷积核大小为1x3x3x1, 共有C个, 需要计算乘法次数为: NxHxWx3x3xC+NxHxWxCx1x1xC=NxHxWxCx(9+C), 而分组卷积, 假定分为2组卷积核为C/4x3x3xC/4, 计算乘法次数为: NxHxWxC/4x3x3xC/4x4=NxHxWxCx(9/4xC), 这种情况下, C<=7使, 计算量上分组卷积会更少, 但是至于C更大的时候, 可以再尝试计算. 这里如此描述”更高效”, 作者解释说, 深度可分离卷积当前还没有被大多数深度学习平台有效的实现. 而分组卷积相较而言, 支持更为完善).
架构无关的有效推理也已被一些先前的研究探索。例如,知识蒸馏 [3,15] 训练小型 “学生” 网络,重现大型 “教师” 网络的输出,以降低测试时间成本。动态推理方法 [2,7, 8,17] 将推理自适应于每个特定的测试示例,跳过单元甚至整个层以减少计算。在这里没有探索这种方法,但相信它们可以与CondenseNet一起使用。
可学习组卷积
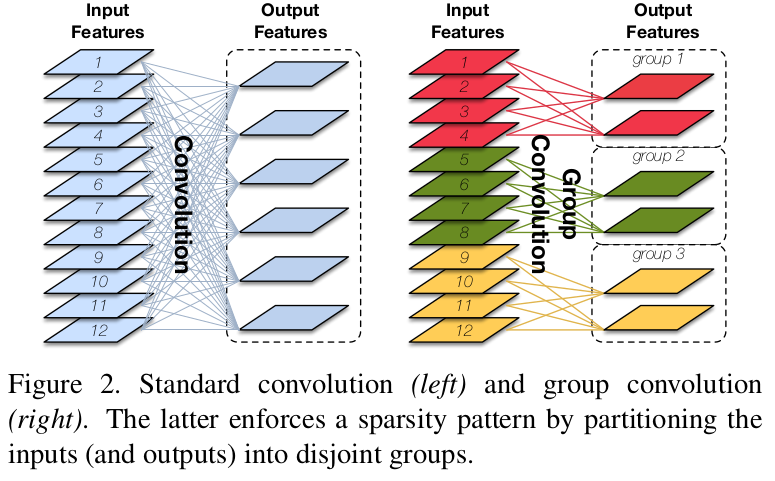
左面是一般的卷积, 可以认为计算损耗是RxO, 其中, R为输入通道数, O为输出通道数. 而右边是分组卷积, 可以认为计算损耗是RxO/G, 减少了G(分组数)倍.
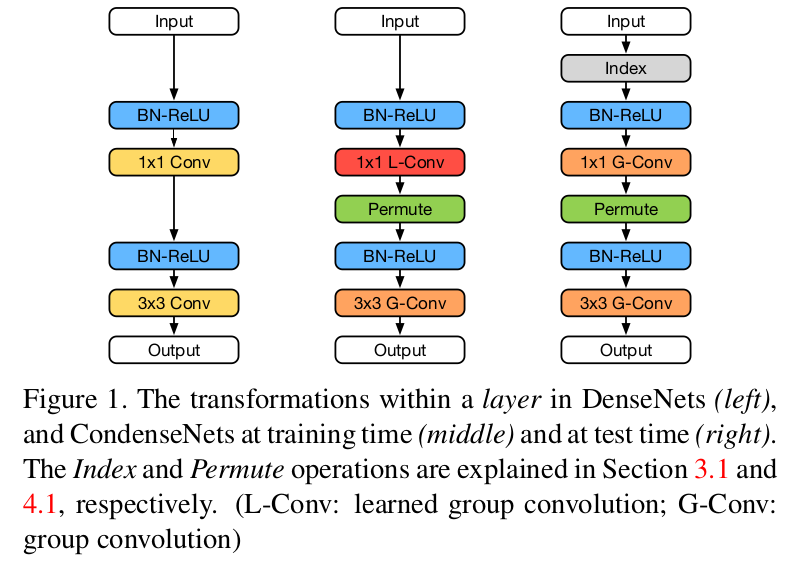
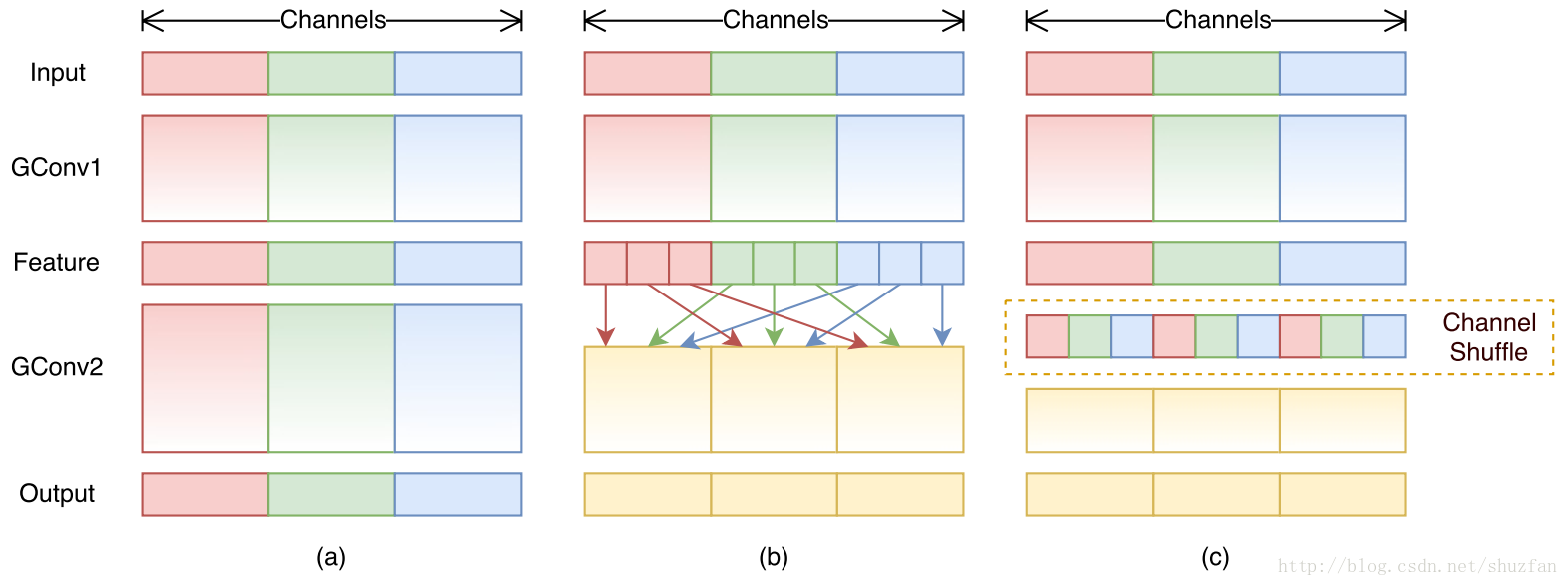
- Figure1中左边图是DenseNet的结构。11 Conv主要起到channel缩减的作用, 33 Conv生成k个channel的输出。
- Figure1中间图是CondenseNet在训练时候的结构,Permute层的作用是为了降低引入1*1 L-Cconv对结果的不利影响,实现的是channel之间的调换过程。
- 11 Conv => 11 L-Conv(learned group convolution)
- 33 Conv => 33 G-Conv(group convolution)
- Figure1中右边图是CondenseNet测试时候的结构,其中的Index层的作用在于feature selection,具体要选择哪些feature map,是在Figure1中间图中训练完的时候就确定的,因此index层只是一个类似0-1操作。
- 由于添加了Index层,所以原来Figure1中间图中的11 L-Conv层在Figure1右边图中替换成常规的卷积group层:11 G-Conv,这是训练和测试时候的一个不同点。
Learn Group Convolution,这个和普通的group convolution有什么不同呢?
这得从11卷积讲起。 作者想要在DenseNet的卷积操作中引入group,在33卷积中问题不大,但是在11卷积中发现直接这样做对最后的结果影响较大,作者推测原因是:_We surmise that this is caused by the fact that the inputs to the 11 layer are concatenations of feature maps generated by preceding layers. Therefore, they differ in two ways from typical inputs to convolutional layers: 1. they have an intrinsic order; and 2.they are far more diverse. _什么意思呢?个人理解:一般1*1卷积层的作用是对前面层的输出特征做channel上的融合,因此如果加入group,那么融合的输入就少了许多,因此输出的多样性就得不到保证。所以如果能弄个像ShuffleNet那样的shuffle操作,就能增加输出多样性。因此作者通过添加Permute层(该层是变换通道顺序的作用,类似shuffle操作,这样后面每个group的33卷积的输入就可以包含11卷积的所有group输出),这可以在一定程度上降低在11卷积中引入group操作对结果的影响.当然作者也说了,虽然使用随机变换, *这样做的效果还是不如相同计算量下的直接用更小的DenseNet网络的效果。
之前的文章中表示,对于有效的特征重用而言, 使用可以获得的早期特征作为后面层的输入, 是有效的. 虽然不是所有的先验特征在每个后续层都需要,而且很难预测哪些特征应该利用在什么时候。为了解决这个问题,我们开发了一种在训练过程中自动学习输入特征分组的方法。学习分组结构允许每个铝箔器组选择自己的一组最相关的输入。此外,我们允许多个组共享输入特征,也允许特征被所有组忽略。
这样就和传统的分组卷积不一样了, 传统的分组中是不允许跨组使用特征的. shufflenet就是对于各组进行抽取重排, 获得了一定的效果.
请注意,在 DenseNet 中,即使输入特征被特定层中的所有组忽略,它仍然可以被不同层的某些组使用。为了区分它与一般的组卷积,我们将我们的方法称为学习组卷积(learned group convolution)。
提出的新的组卷积配合DenseNet的特殊结构, 会使得特征的利用更为灵活.
如何修剪
在训练过程中,逐渐为每一组筛选出不那么重要的输入特征子集。
滤波器组g的第j个输入特征图的重要性是通过组内与之关联所有输出对应的权重的平均绝对值来评估的,即, 其中的
表示组g内第j个输入与第i个输出之间的权重. 本质上就是在求L1范数.
换句话说,如果中的某一列的L1范数小于其他列的L1范数,我们就删除它们(通过将它们归零)。这将导致卷积层在结构上是稀疏的: 来自相同组的滤波器总是接收相同的特征集作为输入.
训练测试过程
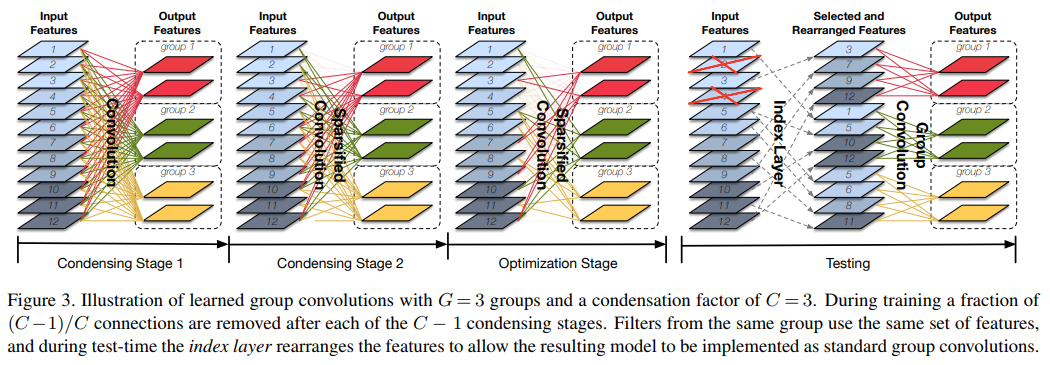
正常的分组卷积,只要输入通道数确定了,那么每一组的输入通道数也就固定了。如,输入通道为256,分为4组,那么每一组的输入通道为256/4=64。 论文设置了一个condensation factor。这个因子的作用是什么呢,举个例子:假设输入通道总数为12,condensation factor=4,分成3组,那么每一组的输入通道数为12/4=3(正常的分组卷积,每一组的输入通道数应该为12/3=4)。也就是这个condensation fractor控制着每一个分组的输入通道数,这样就能够进一步压缩网络, 方便以分组内部滤波器的角度来控制输入通道数.
图中的condensation factor=3,这样一共有3个训练阶段。分别是:
- 一开始的condensing stage 1,这个阶段没有进行裁剪。
- Condensing Stage 2,这个阶段裁剪了1/3 的卷积核(从1223到823)。
- 以及最后的Optimization Stage,这个阶段将卷积核个数裁剪到剩下(1/C=1/3)。也就是按照图片文字描述的, 在(C-1=2)步之后, 移除了(C-1=2)/(C=3)的连接.
我们可以看到:
- 训练阶段可学习的分组卷积最后的每一组的输入通道是会有交叉的。
- 在测试的时候,将剩下的输入特征图rearray一下,就能用正常的分组卷积操作了。
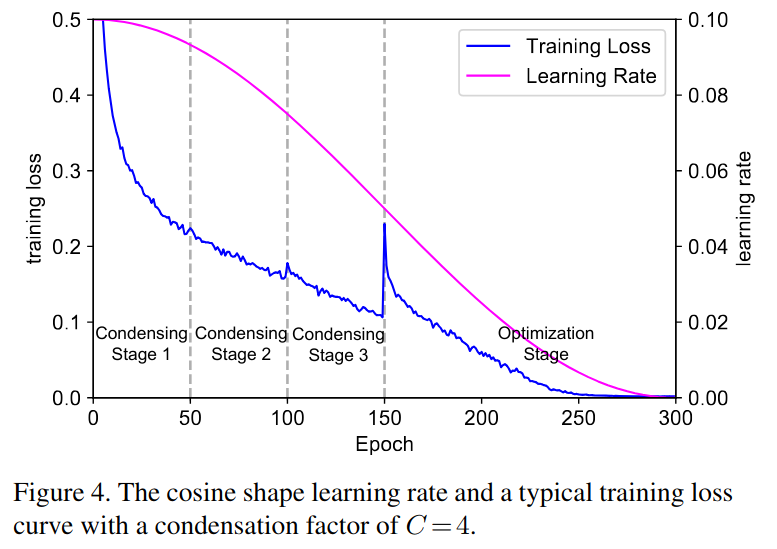
- 训练迭代的前半部分包括condensing阶段。在这里,我们反复训练网络,引入稀疏性,进行固定次数的迭代,然后丢弃不重要的低权重滤波器。
- 训练的后半部分包括优化阶段. 在分组固定后,我们学习滤波器。执行剪枝时,我们确保来自同一组的过滤器共享相同的稀疏模式。
- 因此,一旦训练完成(测试阶段),可以使用标准组卷积来实现稀疏化层。由于许多深度学习库有效地实现了分组卷积,因此在理论和实践中都可以高度节省计算。
这给出了具体的学习率和损失的对应曲线. 其中在150epoch的时候, 开始进入优化阶段, 损失的突然增加是由于最后的condensing操作造成的,该操作去掉了剩余权重的一半。然而,从图中可以看出,模型在优化阶段逐渐从这一修剪步骤中恢复过来。
在我们所有的实验中,我们将每个condensing阶段(一共有C-1个)的训练时间设置为M/(2x(C-1)),其中M表示训练总周期数. 这样训练时间的前半部分用于condenseing。在训练过程的后半部分,即优化阶段,我们对稀疏模型进行了训练. 这里使用的是余弦形式的学习率衰减, 可以平滑地退火学习率.
实现与论文的差异
在我们的训练过程的实现中,我们实际上并没有删除修剪后的权值,而是用一个同样大小的二元掩码张量M用元素级乘法来屏蔽滤波器F。掩码初始化时仅使用1,并且将与修剪权值对应的元素设置为零。这种通过屏蔽的实现在gpu上更有效, 因为不需要稀疏矩阵运算。在实际操作中,这样的剪枝几乎不会增加训练中执行向前以及向后传递所需的挂钟时间时间。
wall time字面意思是挂钟时间,实际上就是指的是现实的时间
group-lasso正则化器
为了减少权值剪枝对精度带来的负面影响,通常采用L1正则化来产生稀疏性[29,32]。在CondenseNet中,我们鼓励来自相同组的卷积过滤器使用相同的输入特征子集,即引入组级稀疏性(group-level sparsity)。为此,我们在训练中使用了下面的group-lasso正则化器[Model selection and estimation in regression with grouped variables]: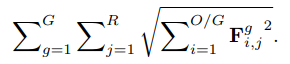
相当于就是对所有的分组, 所有的输入特征进行累计计算总体的L1范数结果. group-lasso正则化器同时将F^g一列的所有元素都推到零,因为平方根项由该列中最大的元素控制。这就导致了我们所追求的组稀疏性.
索引层的使用
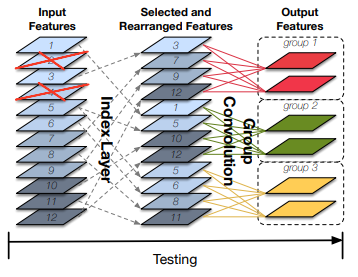
经过训练后,我们删除修剪后的权值,并将稀疏模型转换为具有规则连接模式的网络,该网络可以有效地部署在计算能力有限的设备上。因此,我们引入了一个索引层,它实现了特征选择和重新排序操作(参见图3,右侧)。
索引层输出中的卷积滤波器被重新排列,以适应现有的(高度优化的)正则组卷积实现。
图1显示了训练期间(中间)和测试期间(右边)CondenseNet层的转换。在训练过程中,1x1个卷积是一个learned group convolution(L-Conv),但在测试过程中,在索引层的帮助下,它变成了一个standard group convolution(G-Conv)。
其他的设计
除了上面介绍的使用学习组卷积外,我们还对常规DenseNet体系结构做了两个更改。这些更改旨在进一步简化体系结构并提高其计算效率。图5说明了我们对DenseNet体系结构所做的两个更改.
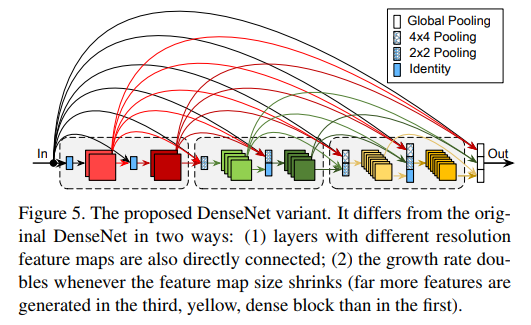
- 不同block的feature map也相互连接(DenseNet中只有一个block内部的几个层之间有dense connection)
- 在Figure5中看到一些22 pooling或44pooling层就是为了解决不同block的feature map连接时候的尺寸问题
- 相比比原DenseNet架构, 这里更加鼓励特征重用. 输入层连接到所有后续网络层中, 即使这些层位于不同的dense块(见图5). 因为密集的block有不同的特征分辨率, 在这里对高分辨率特征图使用平均池化来下采样到较低分辨率。
- 另一个是随着网络的加深增大了growth rate
- growth rate是DenseNet中每一层的输出channel数量
- 假设有m个block,k0为常量(也是第0个block的growth rate), 那么第m个block的growth rate就是:
。因此最终的结果就是加宽了网络。
- 如[Densely connected convolutional networks]所示,DenseNet中更深的层更倾向于依赖高级特性,而不是低级特性。这促使我们通过加强短期联系来改善网络。我们发现这可以通过随着深度的增加而逐渐增加增长率来实现。这种设置增长率的方法不会引入任何额外的超参数。增长速率(IGR)策略增加了来自较靠后的层的特征相对于来自较靠前层的特征的比例。这大大提高了计算效率,但在某些情况下可能会降低参数效率。根据特定的硬件限制,权衡两者可能是有利的.
ImageNet上的结构
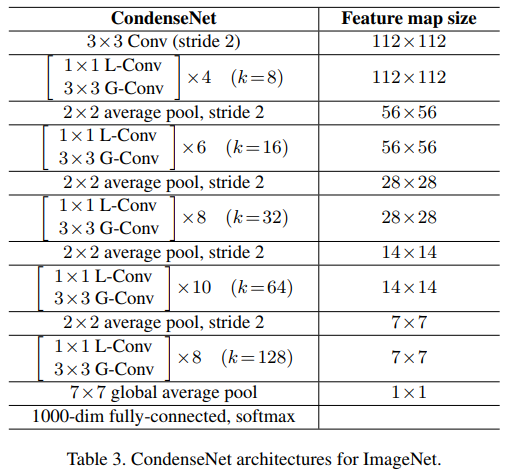
表现
实验在CIFAR-10,CIFAR-100和ImageNet(ILSVRC 2012)数据集上进行。
组件分析
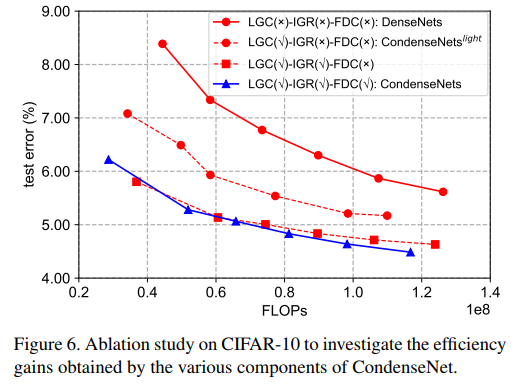
首先是验证前面提到的一些操作的效果,分别是LGC(learned group convolution)、IGR(increasing learning rate)和FDC(full dense connectivity)。可以看出三者都不加的情况就是原来的DenseNet网络,三者都加的情况就是本文的CondenseNet,前两者效果还是比较明显的,FDC的提升比较有限。
和其他结构的比较
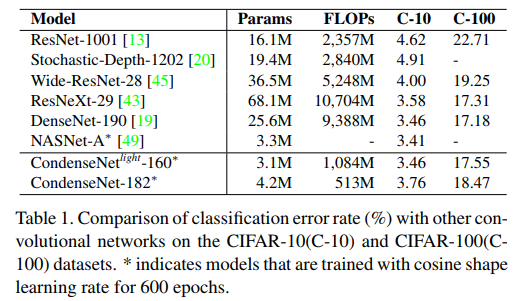
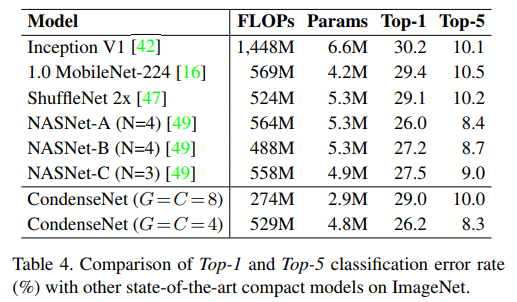
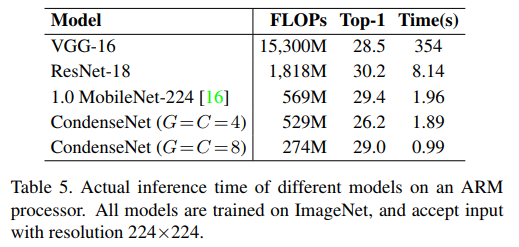
和目前优秀算法的对比,可以看出在基本不影响准确率的情况下,参数量和计算量的下降还是比较明显的
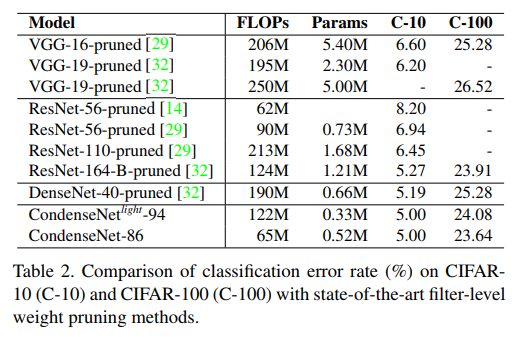
和其他基于filter的剪枝算法的对比。