image.png

主要工作

这是图森的一篇工作。

首先训练好较大的teacher模型，再开始训较小的student模型。不同于hinton那篇文章在最后output层做constraint，这篇文章在student模型和teacher模型的feature maps之间计算一个Maximum Mean Discrepancy作为constraint，希望student模型的features和teachers的尽可能相似。自然，这样的student模型可以有接近teacher的性能，同时保持较少的参数，于是实现了model compression。【参考自“相关链接”中的知乎回答】

主要结构

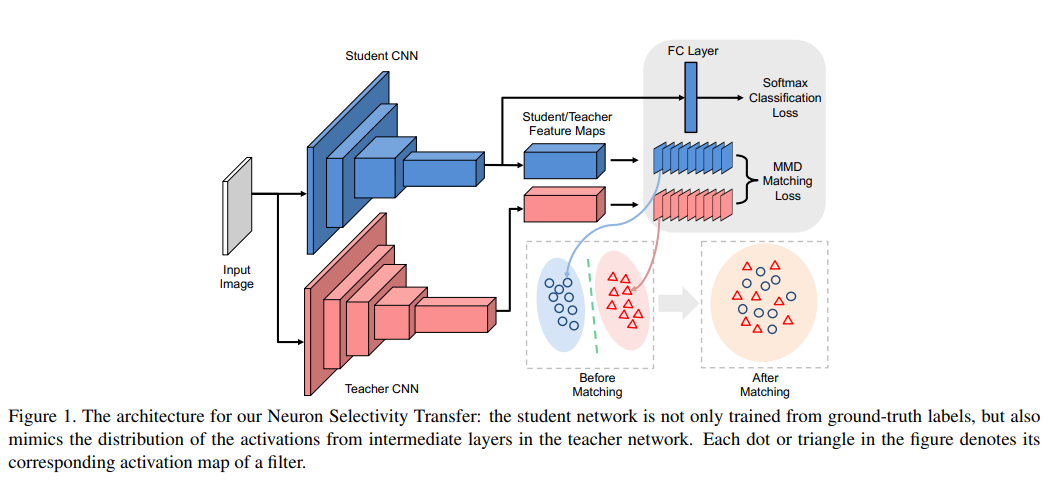
image.png

损失函数

关键在于这里的MMD，MMD 是用来衡量sampled data之间分布差异的距离量度。假设有两个样本集(Arxiv 2017) Like What You Like - Knowledge Distill via Neuron Selectivity Transfer - 图3和(Arxiv 2017) Like What You Like - Knowledge Distill via Neuron Selectivity Transfer - 图4，分别采样自分布p和q，那么p和q对应的平方MMD（最大均值差异）距离可以表示为：
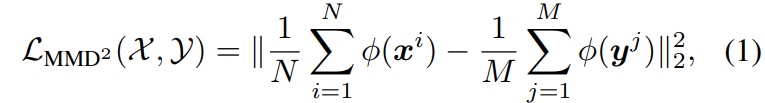
image.png
这里的(Arxiv 2017) Like What You Like - Knowledge Distill via Neuron Selectivity Transfer - 图6是一个显式映射函数，通过进一步扩展，并使用kernel trick，(Arxiv 2017) Like What You Like - Knowledge Distill via Neuron Selectivity Transfer - 图7，可以重新表示为：
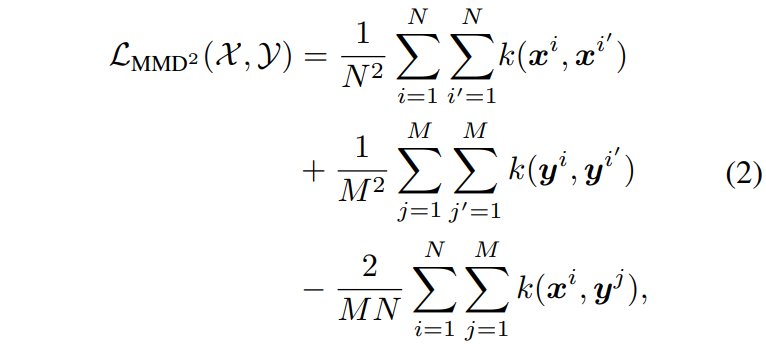
image.png
这里的(Arxiv 2017) Like What You Like - Knowledge Distill via Neuron Selectivity Transfer - 图9表示一个核函数，将样本矢量映射到一个更高或者无限维的特征空间中。

因为当特征空间对应于一个一般的RKHS（再生核希尔伯特空间）时，MMD损失当且仅当p=q时为零，最小化MMD等价于最小化p和q的距离。从而可以使用MMD来衡量Student模型和Teacher模型中间输出的激活feature map的相似程度。通过优化这个损失函数，使得S的输出分布接近T。

通过引入MMD，将NST loss定义如下，下标S表示Student的输出，T表示Teacher的输出。第一项H是指由样本类别标签计算的CrossEntropy Loss。第二项即为上述的MMD Loss。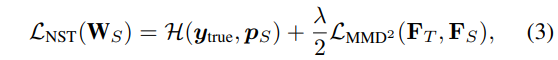
image.png

Considering the activation of each spatial position as one feature, then the flattened activation map of each filter is an sample the space of neuron selectivities of dimension HW. 可以知道，这里的 **f=F.view(N, C, -1)**

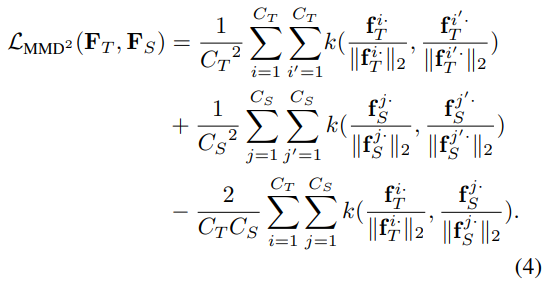
image.png
这里使用fk的L2归一化版本替换了原始的fk，来确保每个样本有着相同的尺度。最小化MMD损失等价于从教师向学生迁移neuron selectivity knowledge。

关于核函数的选择，这里考虑了三种情况。
image.png

相关链接