(NIPS 2017) Learning Efficient Object Detection Models with Knowledge Distillation

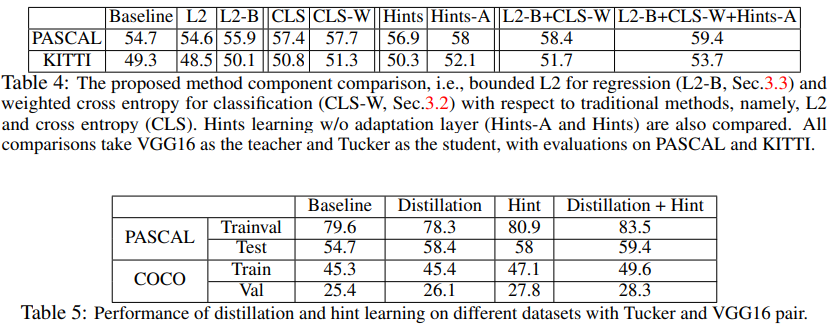
这是NIPS 2017的一篇文章。使用了蒸馏学习处理目标检测问题。

主要工作

这里以Faster RCNN为基础，使用蒸馏学习来得到一个小网络。主要使用的蒸馏的方法都是已有的，包括soft target、hint learing，只是这里：

1. 将其迁移到了目标检测网络中
2. 对其进行了修改：
   1. 使用adaptation调整特征使用hint learning
   2. 使用学生与教师之间的加权交叉熵作为原始的分类交叉熵的辅助损失
   3. 使用教师损失作为上界，辅助原始的用于回归的平滑L1损失

主要结构

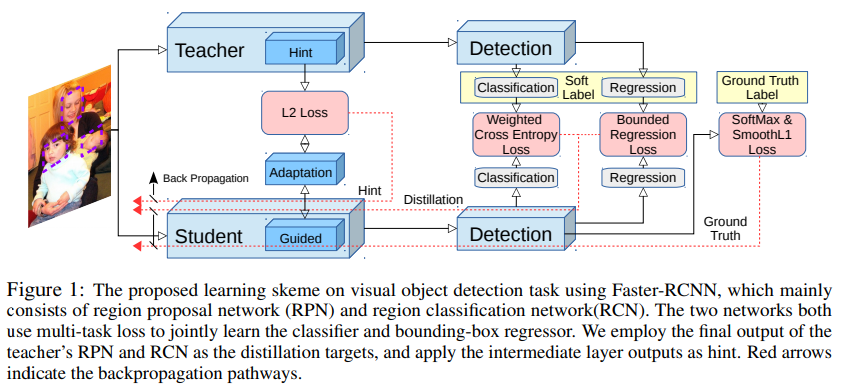
损失函数

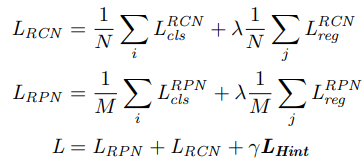
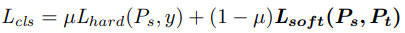
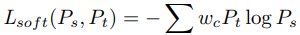
由于检测器需要鉴别的不同类别之间存在样本不均衡（imbalance），因此在中需要对不同类别的交叉熵分配不同的权重，其中背景类的权重为1.5（较大的比例），其他分类的权重均为1.0。In the above, λ and γ are hyper-parameters to control the balance between different losses. We fix them to be 1 and 0.5, respectively, throughout the experiments.

这里的温度参数设置为1，文章的分析： When Pt is very similar to the hard label, with probability for one class very close to 1 and most others very close to 0, the temperature parameter T is introduced to soften the output. Using higher temperature will force t to produce softer labels so that the classes with near-zero probabilities will not be ignored by the cost function. This is especially pertinent to simpler tasks, such as classification on small datasets like MNIST. But for harder problems where the prediction error is already high, a larger value of T introduces more noise which is detrimental to learning. Thus, lower values of T are used in [20] for classification on larger datasets. For even harder problems such as object detection,

we find using no temperature parameter at all (equivalent to T = 1) in the distillation loss works the

best in practice (see supplementary material for an empirical study).

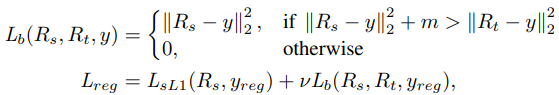
Unlike distillation for discrete categories, the teacher’s regression outputs can provide very wrong guidance toward the student model, since the real valued regression outputs are unbounded. In addition, the teacher may provide regression direction that is contradictory to the ground truth direction. Thus, instead of using the teacher’s regression output directly as a target, we exploit it as an upper bound for the student to achieve. The student’s regression vector should be as close to the ground truth label as possible in general, but once the quality of the student surpasses that of the teacher with a certain margin, we do not provide additional loss for the student. We call this the teacher bounded regression loss, Lb. The teacher bounded regression loss Lb only penalizes the network when the error of the student is larger than that of the teacher. Note that although we use L2 loss inside Lb, any other regression loss such as L1 and smoothed L1 can be combined with Lb. Our combined loss encourages the student to be close to or better than teacher in terms of regression, but does not push the student too much once it reaches the teacher’s performance.

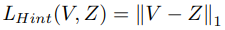
实验效果

相关链接

• 论文：https://papers.nips.cc/paper/6676-learning-efficient-object-detection-models-with-knowledge-distillation.pdf
• 解析：https://blog.csdn.net/nature553863/article/details/82463249