• 【2017-01-30】Adam：A method for stochastic optimization
• We have introduced a simple and computationally efficient algorithm for gradient-based optimization of stochastic objective functions. Our method is aimed towards machine learning problems with large datasets and/or high-dimensional parameter spaces. The method combines the advantages of two recently popular optimization methods:
  • the ability of AdaGrad to deal with sparse gradients
  • and the ability of RMSProp to deal with non-stationary objectives.

• The method is straightforward to implement and requires little memory. The experiments confirm the analysis on the rate of convergence in convex problems. Overall, we found Adam to be robust and well-suited to a wide range of non-convex optimization problems in the field machine learning.

  0、背景介绍

• Stochastic gradient-based optimization is of core practical importance in many fields of science and engineering. Many problems in these fields can be cast as the optimization of some scalar parameterized objective function requiring maximization or minimization with respect to its parameters.

• If the function is differentiable（可微分的） w.r.t.（with respect to，关于；谈及，谈到）its parameters, gradient descent is a relatively efficient optimization method, since the computation of first-order partial derivatives（一阶偏微分方程）w.r.t. all the parameters is of the same computational complexity as just evaluating the function.
• Often, objective functions are stochastic（随机的）. For example, many objective functions are composed of a sum of subfunctions evaluated at different subsamples of data; in this case optimization can be made more efficient by taking gradient steps w.r.t. individual subfunctions, i.e. stochastic gradient descent (SGD) or ascent.
• SGD（随机梯度下降）proved itself as an efficient and effective optimization method that was central in many machine learning success stories, such as recent advances in deep learning.

• Objectives may also have other sources of noise than data subsampling（次取样，分阶抽样）, such as dropout regularization. For all such noisy objectives, efficient stochastic optimization techniques are required.

  1、本文方法

• The focus of this paper is on the optimization of stochastic objectives with high-dimensional parameters spaces. In these cases, higher-order optimization methods are ill-suited（不合适）, and discussion in this paper will be restricted to first-order methods.

• We propose Adam, a method for efficient stochastic optimization that only requires first-order gradients with little memory requirement.

  • The method computes individual adaptive learning rates for different parameters from estimates of first and second moments of the gradients.
  • The name _Adam _is derived from adaptive moment estimation.
  • Our method is designed to combine the advantages of two recently popular methods:
    • AdaGrad：works well with sparse gradients
      • 【2011-00-00】Adaptive Subgradient Methods for Online Learning and Stochastic Optimization
    • RMSProp：works well in on-line and non-stationary settings
  • Some of Adam’s advantages are that the magnitudes of parameter updates are invariant to rescaling of the gradient, its stepsizes are approximately bounded by the stepsize hyperparameter, it does not require a stationary objective, it works with sparse gradients, and it naturally performs a form of step size annealing（退火）.

    （1）Adam 算法（Algorithm 1）：pseudo-code

    

• 参数解析

  • indicates the elementwise square
  • Good default settings for the tested machine learning problems are：、、、
  • All operations on vectors are element-wise
  • 和：andto the power
  • ：a noisy objective function（a stochastic scalar function）that is differentiable w.r.t. parameters
    • ：the expected value of ，We are interested in minimizing it w.r.t. its parameters
    • ：the realisations of the stochastic function at subsequent timesteps，The stochasticity might come from the evaluation at random subsamples (minibatches) of datapoints, or arise from inherent function noise
  • ：the gradient, i.e. the vector of partial derivatives of, w.r.tevaluated at timestep
• The algorithm updates exponential moving averages of the gradient () and the squared gradient () where the hyper-parameterscontrol the exponential decay rates of these moving averages.
  • The moving averages themselves are estimates of themoment (the mean) and the raw moment (the uncentered variance) of the gradient.
  • However, these moving averages are initialized as (vectors of) 0’s, leading to moment estimates that are biased towards zero, especially during the initial timesteps, and especially when the decay rates are small (i.e. theare close to 1).
  • The good news is that this initialization bias can be easily counteracted, resulting in bias-corrected estimatesand。参见：（3）Initialization Bias Correction
• Note that the efficiency of algorithm 1 can, at the expense of clarity, be improved upon by changing the order of computation, e.g. by replacing the last three lines in the loop with the following lines:

and

（2）Adam’s update rule

• An important property of Adam’s update rule is its careful choice of stepsizes.
• Assuming：
  • the effective step taken in parameter space at timestep is：

• The effective stepsize has two upper bounds:
  • 当时：
    • 
    • only happens in the most severe case of sparsity：when a gradient has been zero at all timesteps except at the current timestep
  • 当时：
    • 
    • For less sparse cases, the effective stepsize will be smaller.
  • 当时：
    • 由于，因此
• 通常情况下，因为
• The effective magnitude of the steps taken in parameter space at each timestep are approximately bounded by the stepsize setting，i.e.,
  • This can be understood as establishing a _trust region _around the current parameter value, beyond which the current gradient estimate does not provide sufficient information.
  • This typically makes it relatively easy to know the right scale ofin advance.
    • For many machine learning models, for instance, we often know in advance that good optima are with high probability within some set region in parameter space; it is not uncommon, for example, to have a prior distribution over the parameters.
    • Sincesets (an upper bound of) the magnitude of steps in parameter space, we can often deduce the right order of magnitude ofsuch that optima can be reached fromwithin some number of iterations.
    • With a slight abuse of terminology, we will call the ratiothe signal-to-noise _ratio (_SNR).
    • With a smaller SNR the effective stepsizewill be closer to zero.
• This is a desirable property, since a smaller SNR means that there is greater uncertainty about whether the direction ofcorresponds to the direction of the true gradient.
• For example, the SNR value typically becomes closer to 0 towards an optimum, leading to smaller effective steps in parameter space: a form of automatic annealing.
  • The effective stepsizeis also invariant to the scale of the gradients; rescaling the gradientswith factorwill scalewith a factorandwith a factor，which cancel out：

    （3）Initialization Bias Correction

• Adam utilizes initialization bias correction terms. We will here derive the term for the second moment estimate; the derivation for the first moment estimate is completely analogous.
• Letbe the gradient of the stochastic objective, and we wish to estimate its second raw moment (uncentered variance) using an exponential moving average of the squared gradient, with decay rate.
• Letbe the gradients at subsequent timesteps, each a draw from an underlying gradient distribution
• Let us initialize the exponential moving average as(a vector of zeros).
• First note that the update at timestepof the exponential moving averagecan be written as a function of the gradients at all previous timesteps:
  • 
• We wish to know how（the expected value of the exponential moving average at timestep）relates to the true second moment, so we can correct for the discrepancy（差异）between the two.
• 根据以上公式，可得：
  • 

    - ![](https://cdn.nlark.com/yuque/__latex/71a78217bae64ffb9362bdae14a8b5fe.svg#card=math&code=%3D%5Cmathbb%7BE%7D%5Bg_t%5E2%5D%20%5Ccdot%20%281-%5Cbeta_2%29%5Csum_%7Bi%3D1%7D%5E%7Bt%7D%5Cbeta_2%5E%7Bt-i%7D%2B%5Czeta%20&id=eT8Pk)
    - ![](https://cdn.nlark.com/yuque/__latex/2b46f22729d540cbc108de9cff6aecfd.svg#card=math&code=%3D%5Cmathbb%7BE%7D%5Bg_t%5E2%5D%20%5Ccdot%20%281-%5Cbeta_2%5E%7Bt%7D%29%2B%5Czeta%20&id=xGURs)

  • if the true second momentis stationary，，Otherwisecan be kept small since the exponential decay ratecan (and should) be chosen such that the exponential moving average assigns small weights to gradients too far in the past.
  • What is left is the termwhich is caused by initializing the running average with zeros. In algorithm 1 we therefore divide by this term to correct the initialization bias.

• In case of sparse gradients, for a reliable estimate of the second moment one needs to average over many gradients by chosing a small value of; however it is exactly this case of smallwhere a lack of initialisation bias correction would lead to initial steps that are much larger.

  （4）Convergence Analysis

• We analyze the convergence of Adam using the online learning framework proposed in：

  • 【2003-00-00】Online convex programming and generalized infinitesimal gradient ascent
• Given an arbitrary, unknown sequence of convex cost functions ，At each time, our goal is to predict the parameterand evaluate it on a previously unknown cost function.
• Since the nature of the sequence is unknown in advance, we evaluate our algorithm using the regret：the sum of all the previous difference between the online predictionand the best fixed point parameterfrom a feasible setfor all the previous steps.
  • Concretely, the regret is defined as：
    • 
      • 其中，
• Adam hasregret bound（论文附录中进行证明）
• Our result is comparable to the best known bound for this general convex online learning problem.
• We also use some definitions simplify our notation, where：
  • andas theelement.
  • ：a vector that contains thedimension of the gradients over all iterations till，
  • 

• Our following theorem holds when the learning rateis decaying at a rate ofand first moment running average coefficientdecay exponentially with, that is typically close to 1（e.g. ）

  （a）Theorem（定理）

• Assume that the functionhas bounded gradients，，for alland distance between anygenerated by Adam is bounded, ，for any，andsatisfy. Letand. Adam achieves the following guarantee, for all ：

• This Theorem implies when the data features are sparse and bounded gradients, the summation term can be much smaller than its upper bound, in particular if the class of function and data features are in the form of section 1.2 in 【2011-00-00】Adaptive Subgradient Methods for Online Learning and Stochastic Optimization
  • 
  • 
• Their results for the expected valuealso apply to Adam.
• In particular, the adaptive method, such as Adam and Adagrad, can achieve，an improvement overfor the non-adaptive method.
• Decayingtowards zero is important in our theoretical analysis and also matches previous empirical findings, e.g. 【2013-00-00】On the importance of initialization and momentum in deep learning suggests reducing the momentum coefficient in the end of training can improve convergence.

• Finally, we can show the average regret of Adam converges.

  （b）Corollary（推论）

• Assume that the functionhas bounded gradients,，for alland distance between anygenerated by Adam is bounded, ，for any. Adam achieves the following guarantee, for all ：

  • 
  • This result can be obtained by using Theorem above and
  • Thus

    2、stochastic optimization methods 汇总介绍

• RMSProp：

  • 视频讲解：https://www.youtube.com/watch?v=defQQqkXEfE
  • A version with momentum：【2014-06-05】Generating sequences with recurrent neural networks
  • There are a few important differences between RMSProp with momentum and Adam:
    • RMSProp with momentum generates its parameter updates using a momentum on the rescaled gradient
      • RMSProp also lacks a bias-correction term; this matters most in case of a value of close to 1 (required in case of sparse gradients), since in that case not correcting the bias leads to very large stepsizes and often divergence.（论文6.4章节说明，undo）
    • Adam updates are directly estimated using a running average of first and second moment of the gradient.
• AdaGrad：works well for sparse gradients
  • 【2011-00-00】Adaptive Subgradient Methods for Online Learning and Stochastic Optimization
  • Its basic version updates parameters as：

• Note that if we chooseto be infinitesimally（无穷接近）close to 1 from below, then：

• AdaGrad corresponds to a version of Adam with, infinitesimaland a replacement ofby an annealed version, namely：

• Note that this direct correspondence between Adam and Adagrad does not hold when removing the bias-correction terms; without bias correction, like in RMSProp, a infinitesimally close to 1 would lead to infinitely large bias, and infinitely large parameter updates.
  • vSGD
• 【2013-00-00】No more pesky learning rates
  • AdaDelta
• 【2012-12-22】Adadelta：An adaptive learning rate method
  • natural Newton method
  • all setting stepsizes by estimating curvature from first-order information（所有设置步长都是通过从一阶信息中估计曲率来实现的）.
  • Sum-of-Functions Optimizer (SFO)：a quasi-Newton method based on minibatches, but (unlike Adam) has memory requirements linear in the number of minibatch partitions of a dataset, which is often infeasible on memory-constrained systems such as a GPU.
• 【2014-00-00】Fast large-scale optimization by unifying stochastic gradient and quasi-newton methods
  • natural gradient descent (NGD)：employs a preconditioner that adapts to the geometry of the data, sinceis an approximation to the diagonal of the Fisher information matrix.
• 【1998-00-00】Natural gradient works efficiently in learning
• Fisher information matrix：【2014-02-17】Revisiting natural gradient for deep networks
• 注意：Adam also employs a preconditioner, however, Adam’s preconditioner (like AdaGrad’s) is more conservative in its adaption than vanilla NGD by preconditioning with the square root of the inverse of the diagonal Fisher information matrix approximation.

  3、实验结果

• To empirically evaluate the proposed method, we investigated different popular machine learning models, including logistic regression, multilayer fully connected neural networks and deep convolutional neural networks. Using large models and datasets, we demonstrate Adam can efficiently solve practical deep learning problems.
• We use the same parameter initialization when comparing different optimization algorithms. The hyper-parameters, such as learning rate and momentum, are searched over a dense grid and the results are reported using the best hyper-parameter setting.

  （1-U）Logistic Regression

（2-U）Multi-Layer Neural Networks

（3-U）Convolutional Neural Networks

（4）Evaluate the effect of the bias correction terms

• We also empirically evaluate the effect of the bias correction terms（参考第 1 章节内容）.
• 第 2 章节中表明：removal of the bias correction terms results in a version of RMSProp with momentum.
• We vary theandwhen training a variational autoencoder (VAE) with the same architecture as in (Kingma & Welling, 2013) with a single hidden layer with 500 hidden units with softplus nonlinearities and a 50-dimensional spherical Gaussian latent variable. We iterated over a broad range of hyper-parameter choices, i.e.and, and.
  • Values ofclose to 1, required for robustness to sparse gradients, results in larger initialization bias; therefore we expect the bias correction term is important in such cases of slow decay, preventing an adverse effect on optimization.
• Figure：Effect of bias-correction terms (red line) versus no bias correction terms (green line) after 10 epochs (left) and 100 epochs (right) on the loss (y-axes) when learning a Variational AutoEncoder (VAE), for different settings of stepsize (x-axes) and hyperparametersand .

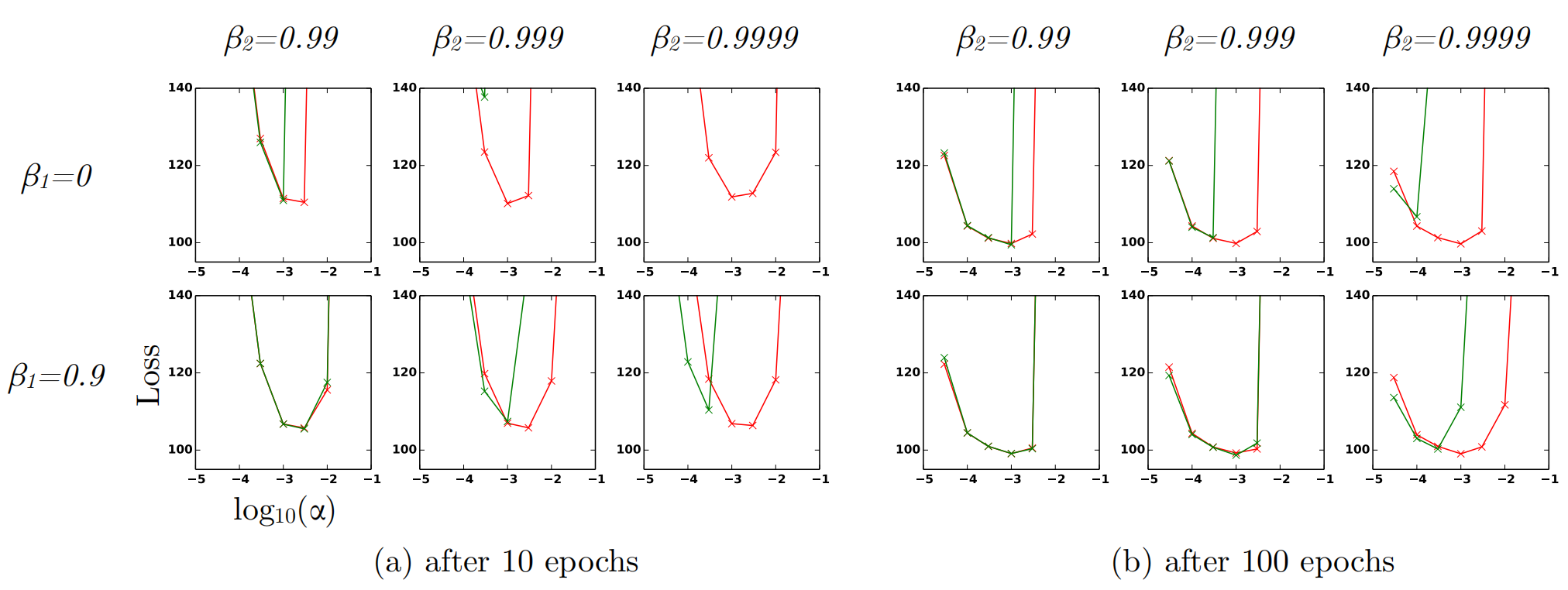
• Figure above shows that, valuesclose to 1 indeed lead to instabilities in training when no bias correction term was present, especially at first few epochs of the training. The best results were achieved with small values ofand bias correction; this was more apparent towards the end of optimization when gradients tends to become sparser as hidden units specialize to specific patterns.
• In summary, Adam performed equal or better than RMSProp, regardless of hyper-parameter setting.

  4、扩展

  （1-U）AdaMax

（2-U）Temporal Averaging

5【undo】、附录：Convergence Proof