2）Computing Gradients
3）Disabling Gradient Tracking
4）More on Computational Graphs
5）Optional Reading: Tensor Gradients and Jacobian Products
2、Autograd Mechanics
Define a train function to be used in different threads
forward
backward
potential optimizer update
User write their own threading code to drive the train_fn
- （1）Registering hooks for a saved tensor
- （2）Registering default hooks for saved tensors

When training neural networks, the most frequently used algorithm is back propagation. In this algorithm, parameters (model weights) are adjusted according to the gradient of the loss function with respect to the given parameter.
To compute those gradients, PyTorch has a built-in differentiation（微分）engine called torch.autograd. It supports automatic computation of gradient for any computational graph.
Consider the simplest one-layer neural network, with input x, parameters w and b, and some loss function. It can be defined in PyTorch in the following manner: ```python import torch

x = torch.ones(5) # input tensor y = torch.zeros(3) # expected output w = torch.randn(5, 3, requires_grad=True) b = torch.randn(3, requires_grad=True) z = torch.matmul(x, w) + b loss = torch.nn.functional.binary_cross_entropy_with_logits(z, y)

<a name="D41hI"></a>
# 1、Automatic Differentiation with torch.autograd
<a name="d6yKJ"></a>
## 1）Tensors, Functions and Computational graph
- This code defines the following computational graph: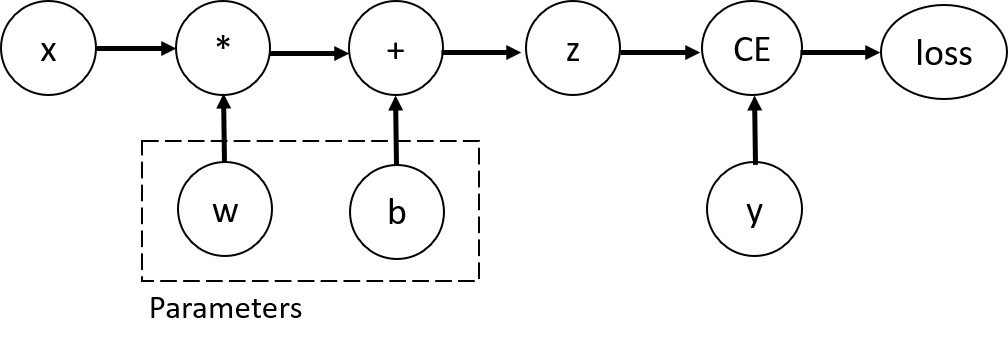
![image.png](https://cdn.nlark.com/yuque/0/2022/png/25833371/1652677285257-99f803cd-d146-4bdd-a98c-77c8fcea02c3.png#clientId=uaa408a49-808f-4&crop=0&crop=0&crop=1&crop=1&from=paste&height=189&id=uf3408a6d&margin=%5Bobject%20Object%5D&name=image.png&originHeight=347&originWidth=1008&originalType=url&ratio=1&rotation=0&showTitle=false&size=31785&status=done&style=none&taskId=u4ec5b87a-af9a-4d45-bf67-eb1f88b3e70&title=&width=548.9970703125)
- In this network, `w` and `b` are parameters, which we need to optimize. Thus, we need to be able to compute the gradients of loss function with respect to those variables. In order to do that, we set the `requires_grad` property of those tensors.
   - You can set the value of `requires_grad` when creating a tensor, or later by using `x.requires_grad_(True)` method.
- A function that we apply to tensors to construct computational graph is in fact an object of class `Function`. This object knows how to compute the function in the _forward_ direction, and also how to compute its derivative during the _backward propagation_ step. A reference to the backward propagation function is stored in `grad_fn` property of a tensor. 
   - more information of `Function`：[https://pytorch.org/docs/stable/autograd.html#function](https://pytorch.org/docs/stable/autograd.html#function)
```python
print(f"Gradient function for z = {z.grad_fn}")
print(f"Gradient function for loss = {loss.grad_fn}")

2）Computing Gradients

To optimize weights of parameters in the neural network, we need to compute the derivatives（导数）of our loss function with respect to parameters, namely, we need andunder some fixed values of x and y.
To compute those derivatives, we call loss.backward(), and then retrieve the values from w.grad and b.grad:
```
loss.backward()
print(w.grad)
print(b.grad)
```
Note：
- We can only obtain the grad properties for the leaf nodes of the computational graph, which have requires_grad property set to True. For all other nodes in our graph, gradients will not be available.
- We can only perform gradient calculations using backward once on a given graph, for performance reasons. If we need to do several backward calls on the same graph, we need to pass retain_graph=True to the backward call.
  3）Disabling Gradient Tracking
By default, all tensors with requires_grad=True are tracking their computational history and support gradient computation. However, there are some cases when we do not need to do that, for example, when we have trained the model and just want to apply it to some input data, i.e. we only want to do forward computations through the network. We can stop tracking computations by surrounding our computation code with torch.no_grad() block: ```python z = torch.matmul(x, w) + b print(z.requires_grad)

with torch.no_grad(): z = torch.matmul(x, w) + b print(z.requires_grad)


- Another way to achieve the same result is to use the `detach()` method on the tensor:
```python
z = torch.matmul(x, w)+b
z_det = z.detach()
print(z_det.requires_grad)

There are reasons you might want to disable gradient tracking:
- To mark some parameters in your neural network as frozen parameters. This is a very common scenario for finetuning a pretrained network。
  - finetuning a pretrained network：https://pytorch.org/tutorials/beginner/finetuning_torchvision_models_tutorial.html
- To speed up computations when you are only doing forward pass, because computations on tensors that do not track gradients would be more efficient.
  4）More on Computational Graphs
Conceptually, autograd keeps a record of data (tensors) and all executed operations (along with the resulting new tensors) in a directed acyclic graph (DAG，有向无环图) consisting of Function objects.
- In this DAG, leaves are the input tensors, roots are the output tensors. By tracing this graph from roots to leaves, you can automatically compute the gradients using the chain rule.
- Function：https://pytorch.org/docs/stable/autograd.html#torch.autograd.Function
In a forward pass, autograd does two things simultaneously:
- run the requested operation to compute a resulting tensor
- maintain the operation’s gradient function in the DAG.
The backward pass kicks off（开始） when .backward() is called on the DAG root. autograd then:
- computes the gradients from each .grad_fn,
- accumulates them in the respective tensor’s .grad attribute
- using the chain rule, propagates all the way to the leaf tensors.
Note：
- DAGs are dynamic in PyTorch
- An important thing to note is that the graph is recreated from scratch; after each .backward() call, autograd starts populating a new graph. This is exactly what allows you to use control flow statements in your model; you can change the shape, size and operations at every iteration if needed.
  5）Optional Reading: Tensor Gradients and Jacobian Products
In many cases, we have a scalar loss function, and we need to compute the gradient with respect to some parameters. However, there are cases when the output function is an arbitrary tensor. In this case, PyTorch allows you to compute so-called Jacobian product, and not the actual gradient.
- Jacobian product：https://zhuanlan.zhihu.com/p/65609544
For a vector function, whereand, a gradient of with respect to is given by Jacobian matrix:

（08）torch.autograd - 图8

Instead of computing the Jacobian matrix itself, PyTorch allows you to compute Jacobian Product （08）torch.autograd - 图9 for a given input vector （08）torch.autograd - 图10 . This is achieved by calling backward with （08）torch.autograd - 图11 as an argument. The size of （08）torch.autograd - 图12 should be the same as the size of the original tensor, with respect to which we want to compute the product:

inp = torch.eye(5, requires_grad=True)
out = (inp+1).pow(2)
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"First call\n{inp.grad}")
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nSecond call\n{inp.grad}")
inp.grad.zero_()
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nCall after zeroing gradients\n{inp.grad}")

Notice that：
- when we call backward for the second time with the same argument, the value of the gradient is different. This happens because when doing backward propagation, PyTorch accumulates the gradients, i.e. the value of computed gradients is added to the grad property of all leaf nodes of computational graph.
- If you want to compute the proper gradients, you need to zero out the grad property before. In real-life training an optimizer helps us to do this.
Note：
- Previously we were calling backward() function without parameters. This is essentially equivalent to calling backward(torch.tensor(1.0)), which is a useful way to compute the gradients in case of a scalar-valued function, such as loss during neural network training.
  2、Autograd Mechanics
参考：https://pytorch.org/docs/stable/notes/autograd.html
This note will present an overview of how autograd works and records the operations. It’s not strictly necessary to understand all this, but we recommend getting familiar with it, as it will help you write more efficient, cleaner programs, and can aid you in debugging.

1）How autograd encodes the history
Autograd is reverse automatic differentiation system.
- Conceptually, autograd records a graph recording all of the operations that created the data as you execute operations, giving you a directed acyclic graph whose leaves are the input tensors and roots are the output tensors.
- By tracing this graph from roots to leaves, you can automatically compute the gradients using the chain rule.
Internally, autograd represents this graph as a graph of Function objects (really expressions), which can be apply() ed to compute the result of evaluating the graph. When computing the forwards pass, autograd simultaneously performs the requested computations and builds up a graph representing the function that computes the gradient (the .grad_fn attribute of each torch.Tensor is an entry point into this graph). When the forwards pass is completed, we evaluate this graph in the backwards pass to compute the gradients.
An important thing to note is that the graph is recreated from scratch at every iteration, and this is exactly what allows for using arbitrary Python control flow statements, that can change the overall shape and size of the graph at every iteration. You don’t have to encode all possible paths before you launch the training - what you run is what you differentiate.

Saved tensors
Some operations need intermediary results to be saved during the forward pass in order to execute the backward pass.
- For example, the functionsaves the inputto compute the gradient.
When defining a custom Python Function, you can use save_for_backward() to save tensors during the forward pass and saved_tensors to retrieve them during the backward pass.
- Function：https://pytorch.org/docs/stable/autograd.html#torch.autograd.Function
- 参考 Extending PyTorch：https://pytorch.org/docs/stable/notes/extending.html
For operations that PyTorch defines (e.g. torch.pow()), tensors are automatically saved as needed. You can explore (for educational or debugging purposes) which tensors are saved by a certain grad_fn by looking for its attributes starting with the prefix _saved.
```
x = torch.randn(5, requires_grad=True)
y = x.pow(2)
print(x.equal(y.grad_fn._saved_self))  # True
print(x is y.grad_fn._saved_self)      # True
```

In the previous code, y.grad_fn._saved_self refers to the same Tensor object as x. But that may not always be the case. For instance:

x = torch.randn(5, requires_grad=True)
y = x.exp()
print(y.equal(y.grad_fn._saved_result))  # True
print(y is y.grad_fn._saved_result)      # False

Under the hood, to prevent reference cycles, PyTorch has packed the tensor upon saving and unpacked it into a different tensor for reading. Here, the tensor you get from accessing y.grad_fn._saved_result is a different tensor object than y (but they still share the same storage).
Whether a tensor will be packed into a different tensor object depends on whether it is an output of its own grad_fn, which is an implementation detail subject to change and that users should not rely on.
- Hooks for saved tensors（参考 “6）” 小节）：control how PyTorch does packing / unpacking.
  2）Locally disabling gradient computation
There are several mechanisms available from Python to locally disable gradient computation:
- To disable gradients across entire blocks of code, there are context managers like no-grad mode and inference mode. For more fine-grained exclusion of subgraphs from gradient computation, there is setting the requires_grad field of a tensor.
Below, in addition to discussing the mechanisms above, we also describe evaluation mode (nn.Module.eval()), a method that is not actually used to disable gradient computation but, because of its name, is often mixed up with the three.

（1）Setting requires_grad
requires_grad is a flag（defaulting to false unless wrapped in a nn.Parameter）that allows for fine-grained exclusion of subgraphs from gradient computation. It takes effect in both the forward and backward passes:
- During the forward pass, an operation is only recorded in the backward graph if at least one of its input tensors require grad.
- During the backward pass (.backward()), only leaf tensors with requires_grad=True will have gradients accumulated into their .grad fields.
It is important to note that：
- even though every tensor has this flag, setting it only makes sense for leaf tensors (tensors that do not have a grad_fn, e.g., a nn.Module’s parameters).
- Non-leaf tensors (tensors that do have grad_fn) are tensors that have a backward graph associated with them. Thus their gradients will be needed as an intermediary result to compute the gradient for a leaf tensor that requires grad. From this definition, it is clear that all non-leaf tensors will automatically have require_grad=True.
Setting requires_grad should be the main way you control which parts of the model are part of the gradient computation.
- For example, if you need to freeze parts of your pretrained model during model fine-tuning.
To freeze parts of your model, simply apply .requires_grad_(False) to the parameters that you don’t want updated.
And as described above, since computations that use these parameters as inputs would not be recorded in the forward pass, they won’t have their .grad fields updated in the backward pass because they won’t be part of the backward graph in the first place, as desired.
Because this is such a common pattern, requires_grad can also be set at the module level with nn.Module.requires_grad_(). When applied to a module, .requires_grad_() takes effect on all of the module’s parameters (which have requires_grad=True by default).

（2）Grad Modes
Apart from setting requires_grad there are also three possible modes enableable from Python that can affect how computations in PyTorch are processed by autograd internally（all of which can be togglable via context managers and decorators）:
- default mode (grad mode)
- no-grad mode
- inference mode
  （a）Default Mode (Grad Mode)
The “default mode” is actually the mode we are implicitly in when no other modes like no-grad and inference mode are enabled.
- To be contrasted with “no-grad mode” the default mode is also sometimes called “grad mode”.
The most important thing to know about the default mode is that：
- it is the only mode in which requires_grad takes effect.
- requires_grad is always overridden to be False in both the two other modes.
  （b）No-grad Mode
Computations in no-grad mode behave as if none of the inputs require grad. In other words, computations in no-grad mode are never recorded in the backward graph even if there are inputs that have require_grad=True.
Enable no-grad mode when you need to perform operations that should not be recorded by autograd, but you’d still like to use the outputs of these computations in grad mode later. This context manager makes it convenient to disable gradients for a block of code or function without having to temporarily set tensors to have requires_grad=False, and then back to True.
- For example, no-grad mode might be useful when writing an optimizer:
  - when performing the training update you’d like to update parameters in-place without the update being recorded by autograd. You also intend to use the updated parameters for computations in grad mode in the next forward pass.
The implementations in torch.nn.init also rely on no-grad mode when initializing the parameters as to avoid autograd tracking when updating the intialized parameters in-place.
- torch.nn.init：https://pytorch.org/docs/stable/nn.init.html#nn-init-doc
  （c）Inference Mode
Inference mode is the extreme version of no-grad mode.
Just like in no-grad mode, computations in inference mode are not recorded in the backward graph, but enabling inference mode will allow PyTorch to speed up your model even more.
- This better runtime comes with a drawback: tensors created in inference mode will not be able to be used in computations to be recorded by autograd after exiting inference mode.
Enable inference mode when you are performing computations that don’t need to be recorded in the backward graph, AND you don’t plan on using the tensors created in inference mode in any computation that is to be recorded by autograd later.
It is recommended that you try out inference mode in the parts of your code that do not require autograd tracking (e.g., data processing and model evaluation).
- If it works out of the box for your use case it’s a free performance win.
- If you run into errors after enabling inference mode, check that you are not using tensors created in inference mode in computations that are recorded by autograd after exiting inference mode.
- If you cannot avoid such use in your case, you can always switch back to no-grad mode.
For details on inference mode：
- https://pytorch.org/cppdocs/notes/inference_mode.html
For implementation details of inference mode：
- https://github.com/pytorch/rfcs/pull/17
  （6）Evaluation Mode (nn.Module.eval())
Evaluation mode is not actually a mechanism to locally disable gradient computation. It is included here anyway because it is sometimes confused to be such a mechanism.
Functionally, module.eval() (or equivalently module.train()) are completely orthogonal to no-grad mode and inference mode.
How model.eval() affects your model depends entirely on the specific modules used in your model and whether they define any training-mode specific behavior.
You are responsible for calling model.eval() and model.train() if your model relies on modules such as torch.nn.Dropout and torch.nn.BatchNorm2d that may behave differently depending on training mode, for example, to avoid updating your BatchNorm running statistics on validation data.
- torch.nn.Dropout：https://pytorch.org/docs/stable/generated/torch.nn.Dropout.html#torch.nn.Dropout
- torch.nn.BatchNorm2d：https://pytorch.org/docs/stable/generated/torch.nn.BatchNorm2d.html#torch.nn.BatchNorm2d
It is recommended that you always use model.train() when training and model.eval() when evaluating your model (validation/testing) even if you aren’t sure your model has training-mode specific behavior, because a module you are using might be updated to behave differently in training and eval modes.

3）In-place operations with autograd
Supporting in-place operations in autograd is a hard matter, and we discourage their use in most cases.
- Autograd’s aggressive buffer freeing and reuse makes it very efficient and there are very few occasions when in-place operations actually lower memory usage by any significant amount.
- Unless you’re operating under heavy memory pressure, you might never need to use them.
There are two main reasons that limit the applicability of in-place operations:
1. In-place operations can potentially overwrite values required to compute gradients.
2. Every in-place operation actually requires the implementation to rewrite the computational graph.
  - Out-of-place versions simply allocate new objects and keep references to the old graph, while in-place operations, require changing the creator of all inputs to the Function representing this operation. This can be tricky, especially if there are many Tensors that reference the same storage (e.g. created by indexing or transposing), and in-place functions will actually raise an error if the storage of modified inputs is referenced by any other Tensor.
    In-place correctness checks
Every tensor keeps a version counter, that is incremented every time it is marked dirty in any operation. When a Function saves any tensors for backward, a version counter of their containing Tensor is saved as well. Once you access self.saved_tensors it is checked, and if it is greater than the saved value an error is raised. This ensures that if you’re using in-place functions and not seeing any errors, you can be sure that the computed gradients are correct.

4）Multithreaded Autograd
The autograd engine is responsible for running all the backward operations necessary to compute the backward pass.
This section will describe all the details that can help you make the best use of it in a multithreaded environment.(this is relevant only for PyTorch 1.6+ as the behavior in previous version was different).
User could train their model with multithreading code (e.g. Hogwild training), and does not block on the concurrent backward computations, example code could be: ```python

Define a train function to be used in different threads
def train_fn(): x = torch.ones(5, 5, requires_grad=True)

forward
y = (x + 3) (x + 4) 0.5

backward
y.sum().backward()

potential optimizer update

User write their own threading code to drive the train_fn

threads = [] for _ in range(10): p = threading.Thread(target=train_fn, args=()) p.start() threads.append(p)

for p in threads: p.join()


- Note that some behaviors that user should be aware of:
<a name="k7qTt"></a>
### （1）Concurrency on CPU

- When you run `backward()` or `grad()` via python or C++ API in multiple threads on CPU, you are expecting to see extra concurrency instead of serializing all the backward calls in a specific order during execution (behavior before PyTorch 1.6).
<a name="ImPAw"></a>
### （2）Non-determinism

- If you are calling `backward()` on multiple thread concurrently but with shared inputs (i.e. Hogwild CPU training). Since parameters are automatically shared across threads, gradient accumulation might become non-deterministic on backward calls across threads, because two backward calls might access and try to accumulate the same `.grad` attribute. This is technically not safe, and it might result in racing condition and the result might be invalid to use.
- But this is expected pattern if you are using the multithreading approach to drive the whole training process but using shared parameters, user who use multithreading should have the threading model in mind and should expect this to happen. User could use the functional API `torch.autograd.grad()` to calculate the gradients instead of `backward()` to avoid non-determinism.
   - `torch.autograd.grad()`：[https://pytorch.org/docs/stable/generated/torch.autograd.grad.html#torch.autograd.grad](https://pytorch.org/docs/stable/generated/torch.autograd.grad.html#torch.autograd.grad)
<a name="JKaoo"></a>
### （3）Graph retaining

- If part of the autograd graph is shared between threads（i.e. run first part of forward single thread, then run second part in multiple threads,） then the first part of graph is shared. In this case different threads execute `grad()` or `backward()` on the same graph might have issue of destroying the graph on the fly of one thread, and the other thread will crash in this case. Autograd will error out to the user similar to what call `backward()` twice with out `retain_graph=True`, and let the user know they should use `retain_graph=True`.
<a name="XUJGc"></a>
### （4）Thread Safety on Autograd Node

- Since Autograd allows the caller thread to drive its backward execution for potential parallelism, it’s important that we ensure thread safety on CPU with parallel backwards that share part/whole of the GraphTask.
- Custom Python `autograd.function` is automatically thread safe because of GIL. for built-in C++ Autograd Nodes(e.g. AccumulateGrad, CopySlices) and custom `autograd::Function`, the Autograd Engine uses thread mutex locking to protect thread safety on autograd Nodes that might have state write/read.
<a name="xyM94"></a>
### （5）No thread safety on C++ hooks

- Autograd relies on the user to write thread safe C++ hooks. If you want the hook to be correctly applied in multithreading environment, you will need to write proper thread locking code to ensure the hooks are thread safe.
<a name="cfu0K"></a>
## 5）Autograd for Complex Numbers

- When you use PyTorch to differentiate any function![](https://cdn.nlark.com/yuque/__latex/98d994c276bf0464fffd664d200efcb4.svg#card=math&code=f%28z%29&id=iIITe)with complex domain and/or codomain, the gradients are computed under the assumption that the function is a part of a larger real-valued loss function![](https://cdn.nlark.com/yuque/__latex/fbd5a9562c50fc729b35f65f5a32d879.svg#card=math&code=g%28input%29%3DL&id=Fpe3k). The gradient computed is![](https://cdn.nlark.com/yuque/__latex/efad87833b97c51f6fdee9c898d485cf.svg#card=math&code=%5Cfrac%7B%5Cpartial%20L%7D%7B%5Cpartial%20z%5E%2A%7D&id=epVmn)(note the conjugation of ![](https://cdn.nlark.com/yuque/__latex/02bab26178a0cd05dae15ad487830237.svg#card=math&code=z&id=MygBu)), the negative of which is precisely the direction of steepest descent used in Gradient Descent algorithm. Thus, all the existing optimizers work out of the box with complex parameters.
- This convention matches TensorFlow’s convention for complex differentiation, but is different from JAX (which computes ![](https://cdn.nlark.com/yuque/__latex/516d594496923ccfe593c9b88b93804e.svg#card=math&code=%5Cfrac%7B%5Cpartial%20L%7D%7B%5Cpartial%20z%7D&id=DSRud)).
- If you have a real-to-real function which internally uses complex operations, the convention here doesn’t matter: you will always get the same result that you would have gotten if it had been implemented with only real operations.
- Mathematical details and how to define complex derivatives in PyTorch are shown below.
<a name="q8Q1S"></a>
### （1）What are complex derivatives?

- The mathematical definition of complex-differentiability takes the limit definition of a derivative and generalizes it to operate on complex numbers. Consider a function![](https://cdn.nlark.com/yuque/__latex/510cd27d03daaabb1aee8d340d71bfc5.svg#card=math&code=f%3A%20%E2%84%82%20%E2%86%92%20%E2%84%82&id=VpZOf)
   - ![](https://cdn.nlark.com/yuque/__latex/ebc6612fb1a9af104d7a66c32624443b.svg#card=math&code=%E2%80%98f%28z%3Dx%2Byj%29%3Du%28x%2Cy%29%2Bv%28x%2Cy%29j%E2%80%98&id=HuIXx)
   - where![](https://cdn.nlark.com/yuque/__latex/77c3adce895348f6083c425fe1ba2624.svg#card=math&code=u&id=jBtJ2)and![](https://cdn.nlark.com/yuque/__latex/a770a282bbfa0ae1ec474b7ed311656d.svg#card=math&code=v&id=ROCM8)are two variable real valued functions.
- Using the derivative definition, we can write:
   - ![](https://cdn.nlark.com/yuque/__latex/976d2f0d20baf08e580a60fb0a048be8.svg#card=math&code=f%5E%E2%80%B2%28z%29%3D%5Clim_%7Bh%E2%86%920%2Ch%E2%88%88C%7D%5Cfrac%7Bf%28z%2Bh%29%E2%88%92f%28z%29%7D%7Bh%7D&id=xGYdG)
- In order for this limit to exist, not only must ![](https://cdn.nlark.com/yuque/__latex/77c3adce895348f6083c425fe1ba2624.svg#card=math&code=u&id=G2jbz)and![](https://cdn.nlark.com/yuque/__latex/a770a282bbfa0ae1ec474b7ed311656d.svg#card=math&code=v&id=qlbXx)must be real differentiable, but![](https://cdn.nlark.com/yuque/__latex/18f3c2855f0e85a1ac2257f64d917144.svg#card=math&code=f&id=vFiTF)must also satisfy the Cauchy-Riemann equations. In other words: the limit computed for real and imaginary steps (![](https://cdn.nlark.com/yuque/__latex/67df0f404d0960fadcc99f6258733f22.svg#card=math&code=h&id=OyzTr)) must be equal. This is a more restrictive condition.
   - Cauchy-Riemann equations：[https://en.wikipedia.org/wiki/Cauchy%E2%80%93Riemann_equations](https://en.wikipedia.org/wiki/Cauchy%E2%80%93Riemann_equations)
- The complex differentiable functions are commonly known as holomorphic functions. They are well behaved, have all the nice properties that you’ve seen from real differentiable functions, but are practically of no use in the optimization world. 
   - For optimization problems, only real valued objective functions are used in the research community since complex numbers are not part of any ordered field and so having complex valued loss does not make much sense.
- It also turns out that no interesting real-valued objective fulfill the Cauchy-Riemann equations. So the theory with homomorphic function cannot be used for optimization and most people therefore use the Wirtinger calculus.
<a name="DywlM"></a>
### （2）Wirtinger Calculus
【undo】[https://pytorch.org/docs/stable/notes/autograd.html#wirtinger-calculus-comes-in-picture](https://pytorch.org/docs/stable/notes/autograd.html#wirtinger-calculus-comes-in-picture)

<a name="QoRjg"></a>
## 6）Hooks for saved tensors

- You can control how saved tensors are packed / unpacked（参考 “1）” 小节） by defining a pair of `pack_hook` / `unpack_hook` hooks. 
   - The `pack_hook` function should take a tensor as its single argument but can return any python object (e.g. another tensor, a tuple, or even a string containing a filename). 
   - The `unpack_hook` function takes as its single argument the output of `pack_hook` and should return a tensor to be used in the backward pass. The tensor returned by `unpack_hook` only needs to have the same content as the tensor passed as input to `pack_hook`. 
- In particular, any autograd-related metadata can be ignored as they will be overwritten during unpacking.
- An example of such pair is:
```python
class SelfDeletingTempFile():
    def __init__(self):
        self.name = os.path.join(tmp_dir, str(uuid.uuid4()))

    def __del__(self):
        os.remove(self.name)

def pack_hook(tensor):
    temp_file = SelfDeletingTempFile()
    torch.save(tensor, temp_file.name)
    return temp_file

def unpack_hook(temp_file):
    return torch.load(temp_file.name)

Notice that：
- The unpack_hook should not delete the temporary file because it might be called multiple times: the temporary file should be alive for as long as the returned SelfDeletingTempFile object is alive.
- In the above example, we prevent leaking the temporary file by closing it when it is no longer needed (on deletion of the SelfDeletingTempFile object).
Note & Warning：
- We guarantee that pack_hook will only be called once but unpack_hook can be called as many times as the backward pass requires it and we expect it to return the same data each time.
- Performing inplace operations on the input of any of the functions is forbidden as they may lead to unexpected side-effects.
  - PyTorch will throw an error if the input to a pack hook is modified inplace but does not catch the case where the input to an unpack hook is modified inplace.
    （1）Registering hooks for a saved tensor
You can register a pair of hooks on a saved tensor by calling the register_hooks() method on a SavedTensor object. Those objects are exposed as attributes of a grad_fn and start with the _raw_saved_ prefix.
- The pack_hook method is called as soon as the pair is registered.
- The unpack_hook method is called each time the saved tensor needs to be accessed, either by means of y.grad_fn._saved_self or during the backward pass.
```
x = torch.randn(5, requires_grad=True)
y = x.pow(2)
y.grad_fn._raw_saved_self.register_hooks(pack_hook, unpack_hook)
```
Warning：
- If you maintain a reference to a SavedTensor after the saved tensors have been released (i.e. after backward has been called), calling its register_hooks() is forbidden. PyTorch will throw an error most of the time but it may fail to do so in some cases and undefined behavior may arise.
  （2）Registering default hooks for saved tensors
Alternatively, you can use the context-manager saved_tensors_hooks to register a pair of hooks which will be applied to all saved tensors that are created in that context. Example:
- saved_tensors_hooks：https://pytorch.org/docs/stable/autograd.html#torch.autograd.graph.saved_tensors_hooks ```python SAVE_ON_DISK_THRESHOLD = 1000

def pack_hook(x):

# Only save on disk tensors that have size >= 1000
if x.numel() < SAVE_ON_DISK_THRESHOLD:
    return x
temp_file = SelfDeletingTempFile()
torch.save(tensor, temp_file.name)
return temp_file

def unpack_hook(tensor_or_sctf): if isinstance(tensor_or_sctf, torch.Tensor): return tensor_or_sctf return torch.load(tensor_or_sctf.name)

class Model(nn.Module): def forward(self, x): with torch.autograd.graph.saved_tensors_hooks(pack_hook, unpack_hook):

      # ... compute output
      output = x
    return output

model = Model() net = nn.DataParallel(model)


- The hooks defined with this context manager are thread-local. Hence, the following code will not produce the desired effects because the hooks do not go through DataParallel.
```python
# Example what NOT to do

net = nn.DataParallel(model)
with torch.autograd.graph.saved_tensors_hooks(pack_hook, unpack_hook):
    output = net(input)

Note that using those hooks disables all the optimization in place to reduce Tensor object creation.
For example:
```
with torch.autograd.graph.saved_tensors_hooks(lambda x: x, lambda x: x):
  x = torch.randn(5, requires_grad=True)
  y = x * x
```
- Without the hooks, x, y.grad_fn._saved_self and y.grad_fn._saved_other all refer to the same tensor object.
- With the hooks, PyTorch will pack and unpack x into two new tensor objects that share the same storage with the original x (no copy performed).

【03】机器学习、深度学习

（08）torch.autograd

2）Computing Gradients

3）Disabling Gradient Tracking

4）More on Computational Graphs

5）Optional Reading: Tensor Gradients and Jacobian Products

2、Autograd Mechanics

1）How autograd encodes the history

Saved tensors

2）Locally disabling gradient computation

（1）Setting `requires_grad`

（2）Grad Modes

（a）Default Mode (Grad Mode)

（b）No-grad Mode

（c）Inference Mode

（6）Evaluation Mode (nn.Module.eval())

3）In-place operations with autograd

In-place correctness checks

4）Multithreaded Autograd

Define a train function to be used in different threads

forward

backward

potential optimizer update

User write their own threading code to drive the train_fn

（1）Registering hooks for a saved tensor

（2）Registering default hooks for saved tensors

（08）torch.autograd

2）Computing Gradients

3）Disabling Gradient Tracking

4）More on Computational Graphs

5）Optional Reading: Tensor Gradients and Jacobian Products

2、Autograd Mechanics

1）How autograd encodes the history

Saved tensors

2）Locally disabling gradient computation

（1）Setting requires_grad

（2）Grad Modes

（a）Default Mode (Grad Mode)

（b）No-grad Mode

（c）Inference Mode

（6）Evaluation Mode (nn.Module.eval())

3）In-place operations with autograd

In-place correctness checks

4）Multithreaded Autograd

Define a train function to be used in different threads

forward

backward

potential optimizer update

User write their own threading code to drive the train_fn

（1）Registering hooks for a saved tensor

（2）Registering default hooks for saved tensors

（1）Setting `requires_grad`