对上述提及模型指标进行公式推导细化，并举例试计算。
在此约定，公式行（1）为数学公式，公式行（2）为数值计算，若其结果不能整除，则保留小数点后4位。
如下：

5.5 模型指标 - 图1

5.5.1 示例模型

这里我们需要准备一个示例模型，用于后续试计算。

  • make_classification()创建二分类数据集；
  • LogisticRegression()创建逻辑回归模型；
  1. import pandas as pd
  2. from sklearn.datasets import make_classification
  3. from sklearn.linear_model import LogisticRegression
  5. X, Y = make_classification(
  6.     n_samples=10000, 
  7.     n_features=1000, 
  8.     n_informative=5, 
  9.     n_redundant=5, 
  10.     flip_y=1)
  11. model = LogisticRegression()
  12. model.fit(X, Y)
  14. print(X.shape, Y.shape)
  15. print(pd.value_counts(Y))
  16. print(pd.value_counts(Y)/pd.value_counts(Y).sum())
  17. """
  18. (10000, 1000) (10000,)
  19. 0    5008
  20. 1    4992
  21. dtype: int64
  22. 0    0.5008
  23. 1    0.4992
  24. dtype: float64
  25. """

现在，我们管这个示例模型叫5.5 模型指标 - 图2。

5.5.2 变量筛选

  • 5.5 模型指标 - 图3、5.5 模型指标 - 图4

对于二分类目标变量，一般用5.5 模型指标 - 图5值(Information Value)以挑选变量。原理公式如下：

Good Bad Good% Bad% 5.5 模型指标 - 图6 5.5 模型指标 - 图7
5.5 模型指标 - 图8#card=math&code=%281%29&id=JLMCl) 5.5 模型指标 - 图9#card=math&code=%282%29&id=fI3QF) 5.5 模型指标 - 图10#card=math&code=log%281%2F2%29&id=h9o0r) 5.5 模型指标 - 图11*WOE#card=math&code=%281-2%29%2AWOE&id=gZb6L)
5.5 模型指标 - 图12 5.5 模型指标 - 图13 5.5 模型指标 - 图14 5.5 模型指标 - 图15 5.5 模型指标 - 图16 5.5 模型指标 - 图17#card=math&code=log%28%5Cfrac%7BG_1%2FG%7D%7BB_1%2FB%7D%29&id=t3I2i) 5.5 模型指标 - 图18%5Ctimes%20log(%5Cfrac%7BG_1%2FG%7D%7BB_1%2FB%7D)#card=math&code=%28G_1%2FG-B_1%2FB%29%5Ctimes%20log%28%5Cfrac%7BG_1%2FG%7D%7BB_1%2FB%7D%29&id=As9Qe)
5.5 模型指标 - 图19 5.5 模型指标 - 图20 5.5 模型指标 - 图21 5.5 模型指标 - 图22 5.5 模型指标 - 图23 5.5 模型指标 - 图24#card=math&code=log%28%5Cfrac%7BG_2%2FG%7D%7BB_2%2FB%7D%29&id=xhPif) 5.5 模型指标 - 图25%5Ctimes%20log(%5Cfrac%7BG_2%2FG%7D%7BB_2%2FB%7D)#card=math&code=%28G_2%2FG-B_2%2FB%29%5Ctimes%20log%28%5Cfrac%7BG_2%2FG%7D%7BB_2%2FB%7D%29&id=oeOjp)
…
5.5 模型指标 - 图26 5.5 模型指标 - 图27 5.5 模型指标 - 图28 5.5 模型指标 - 图29 5.5 模型指标 - 图30 5.5 模型指标 - 图31#card=math&code=log%28%5Cfrac%7BG_N%2FG%7D%7BB_N%2FB%7D%29&id=OWoAL) 5.5 模型指标 - 图32%5Ctimes%20log(%5Cfrac%7BG_N%2FG%7D%7BB_N%2FB%7D)#card=math&code=%28G_N%2FG-B_N%2FB%29%5Ctimes%20log%28%5Cfrac%7BG_N%2FG%7D%7BB_N%2FB%7D%29&id=YZCCT)
5.5 模型指标 - 图33 5.5 模型指标 - 图34 5.5 模型指标 - 图35 5.5 模型指标 - 图36%5Ctimes%20log(%5Cfrac%7BG_i%2FG%7D%7BB_i%2FB%7D)%7D#card=math&code=%5Csum%7B%28%5Cfrac%7BG_i%7D%7BG%7D-%5Cfrac%7BB_i%7D%7BB%7D%29%5Ctimes%20log%28%5Cfrac%7BG_i%2FG%7D%7BB_i%2FB%7D%29%7D&id=ZGbqj)

可解释为衡量特征包含预测变量浓度的指标。

示例如下，该变量各取值5.5 模型指标 - 图37值以及总体5.5 模型指标 - 图38值：

非目标数 目标数 总计 5.5 模型指标 - 图39 5.5 模型指标 - 图40
A61 386 217 603 0.271 0.047
A62 69 34 103 0.140 0.002
A63 52 11 63 -0.707 0.027
A64 42 6 48 -1.099 0.044
A65 151 32 183 -0.704 0.077
5.5 模型指标 - 图41 700 300 1000 0.197

5.5 模型指标 - 图42，有一定预测性。

一般认定，

5.5 模型指标 - 图43

5.5.3 混淆矩阵

5.5.3.1 相关指标

混淆矩阵（Confusion Matrix），以二分类为例，

预测\实际 0 1
0 TN FN
1 FP TP

在模型5.5 模型指标 - 图44上，

预测\实际 0 1
0 3155 1822
1 1853 3170
  • 准确率

5.5 模型指标 - 图45

原则上，准确率越大越好，但并不好量化优劣，毕竟存在模型输出均为0时准确率已达98%（若1占比仅2%）。

  • 精确率

5.5 模型指标 - 图46

  • 召回率

5.5 模型指标 - 图47

精确率与召回率，一般认定追求更高精准率将损失一定的召回率，反之同理。后将辅证之。

  • 5.5 模型指标 - 图48分数

鉴于精确率与召回率的关系，为能同时兼顾，引入精确率和召回率的调和平均数，定义为5.5 模型指标 - 图49分数。

5.5 模型指标 - 图50

更一般的，我们定义5.5 模型指标 - 图51分数：

5.5 模型指标 - 图52%5Cfrac%7Bprecision%20%5Ctimes%20recall%7D%7B(%5Cbeta%20%5E%202%20%5Ctimes%20precision)%2Brecall%7D%0A#card=math&code=F_%5Cbeta%20%3D%20%281%2B%5Cbeta%5E2%29%5Cfrac%7Bprecision%20%5Ctimes%20recall%7D%7B%28%5Cbeta%20%5E%202%20%5Ctimes%20precision%29%2Brecall%7D%0A&id=CP1sl)

除了5.5 模型指标 - 图53分数之外，5.5 模型指标 - 图54分数和5.5 模型指标 - 图55分数在统计学中也得到大量的应用：

其中，5.5 模型指标 - 图56分数中，召回率的权重高于精确率，而5.5 模型指标 - 图57分数中，精确率的权重高于召回率。

  • 5.5 模型指标 - 图58分数

另外的，精确率和召回率的几何平均数定义为5.5 模型指标 - 图59分数。

5.5 模型指标 - 图60

  • 5.5 模型指标 - 图61值

5.5 模型指标 - 图62

5.5 模型指标 - 图63%5Ctimes(TN%2BFP)%2B(TP%2BFN)%5Ctimes(TP%2BFP)%7D%7B(TP%2BTN%2BFP%2BFN)%5E2%7D%20%5C%5C%20%26%3D%5Cfrac%7B(3155%2B1822)%5Ctimes(3155%2B1853)%20%2B%20(3170%2B1822)%5Ctimes(3170%2B1853)%7D%7B10000%5E2%7D%20%5C%5C%0A%26%5Capprox%200.5000%0A%5Cend%7Balign%7D%0A#card=math&code=%5Cbegin%7Balign%7D%0Ap_e%20%26%3D%20%5Cfrac%7B%28TN%2BFN%29%5Ctimes%28TN%2BFP%29%2B%28TP%2BFN%29%5Ctimes%28TP%2BFP%29%7D%7B%28TP%2BTN%2BFP%2BFN%29%5E2%7D%20%5C%5C%20%26%3D%5Cfrac%7B%283155%2B1822%29%5Ctimes%283155%2B1853%29%20%2B%20%283170%2B1822%29%5Ctimes%283170%2B1853%29%7D%7B10000%5E2%7D%20%5C%5C%0A%26%5Capprox%200.5000%0A%5Cend%7Balign%7D%0A&id=nrbce)

5.5 模型指标 - 图64

一般认定，

5.5 模型指标 - 图65

  • 假阳性率5.5 模型指标 - 图66

在所有的负样本中，分类器预测错误的比例：

5.5 模型指标 - 图67

  • 真阳性率5.5 模型指标 - 图68

在所有的正样本中，分类器预测正确的比例：

5.5 模型指标 - 图69

5.5.3.2 相互关系

理论上，这些公式从数学的角度可以推导相互关系，尽管有些比较复杂。

但我们可以应用“大数定律”来模拟：

  1. import random
  2. import pandas as pd
  4. N = 5000
  5. result = []
  7. for _ in range(1000000):
  8.     try:
  9.         TP = random.randint(0, N)
  10.         TN = random.randint(0, N-TP)
  11.         FP = random.randint(0, N-TP-TN)
  12.         FN = N-TP-TN-FP
  14.         A = (TP+TN)/(N)
  15.         P = TP/(TP+FP)
  16.         R = TP/(TP+FN)
  17.         F1 = (2*P*R)/(P+R)
  18.         pe = ((TN+FN)*(TN+FP)+(TP+FN)*(TP+FP))/(N**2)
  19.         K = (A-pe)/(1-pe)
  20.         result.append([TP, TN, FP, FN, A, P, R, F1, pe, K])
  21.     except:
  22.         pass
  24. col = ["TP", "TN", "FP", "FN", "A", "P", "R", "F1", "pe", "K"]
  25. data = pd.DataFrame(result, columns=col)
  26. for icol in col:
  27.     data["_"+icol] = [round(_,1) for _ in data[icol]]

如上我们可以知道：

  • pd.crosstab(data["_P"], data["_R"])

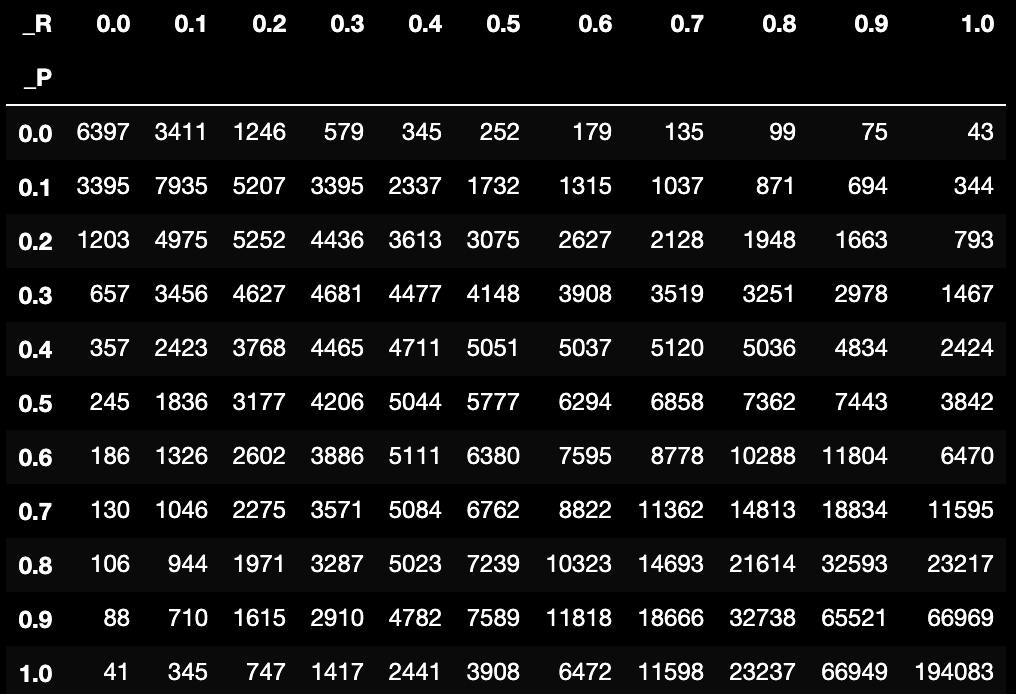
image.png
大部分情况下，追求5.5 模型指标 - 图71值越高则5.5 模型指标 - 图72值越低，反之追求5.5 模型指标 - 图73值越高则5.5 模型指标 - 图74值越低。

  • pd.crosstab(data["_F1"], data["_K"])

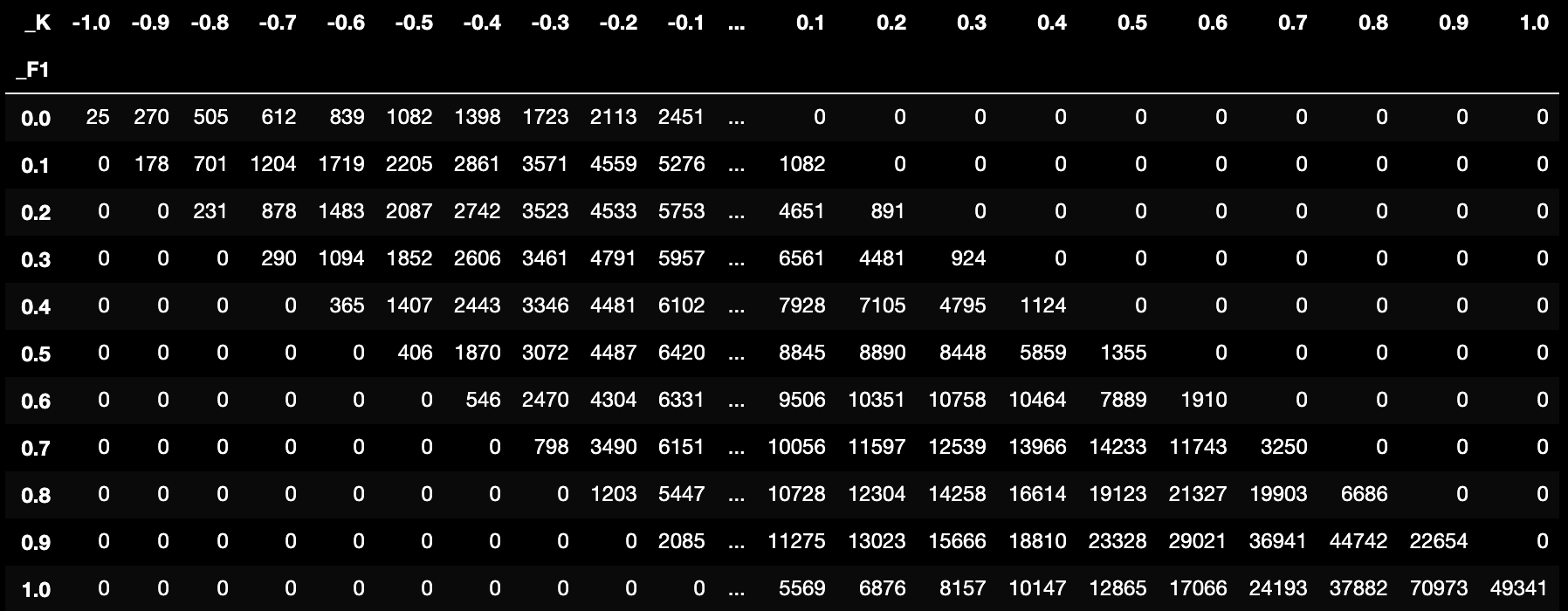
image.png
模型5.5 模型指标 - 图76值越高，5.5 模型指标 - 图77越不可能为负值，更多结论可自行研究。

5.5.4 模型排序性

5.5 模型指标 - 图78即排序性，常用来反映模型的排序能力。在信贷风控业务中，往往需要模型具有良好的排序性，如信用评分模型，业务希望按模型分数对客群进行划分后，分数高的客群的风险低于分数低的客群。
5.5 模型指标 - 图79、5.5 模型指标 - 图80、5.5 模型指标 - 图81等指标常用来衡量模型的排序能力。
在模型5.5 模型指标 - 图82上，根据模型预测概率/评分构建分组，如下：
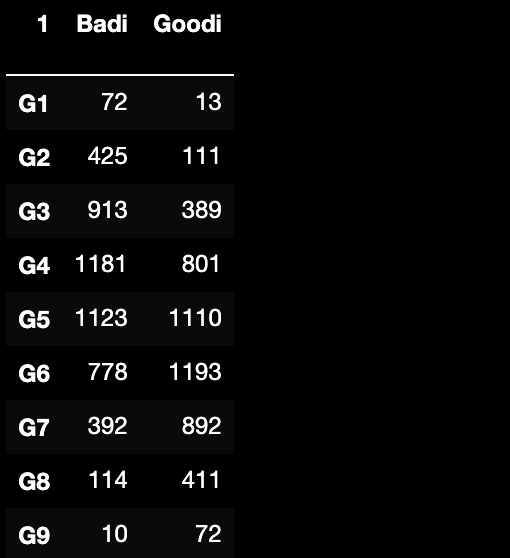
image.png

5.5.4.1 BadRate

5.5 模型指标 - 图84

即坏样本率，分组内坏样本数/分组内全部样本数；
且根据0 0.5008;1 0.4992;可知整体5.5 模型指标 - 图85.
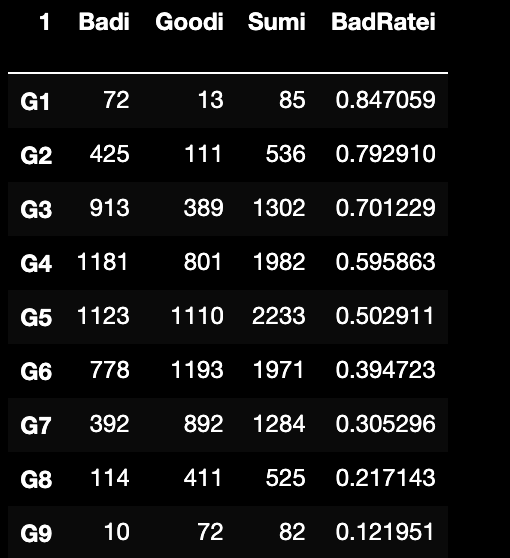
image.png

5.5.4.2 Odds

5.5 模型指标 - 图87

即好坏样本比，分组内坏样本数/分组内好样本数；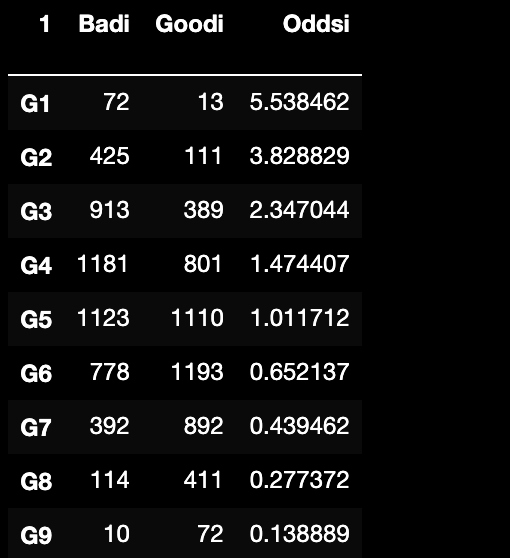
image.png

5.5.4.3 Lift

5.5 模型指标 - 图89

即提升度，分组内5.5 模型指标 - 图90/整体样本5.5 模型指标 - 图91；
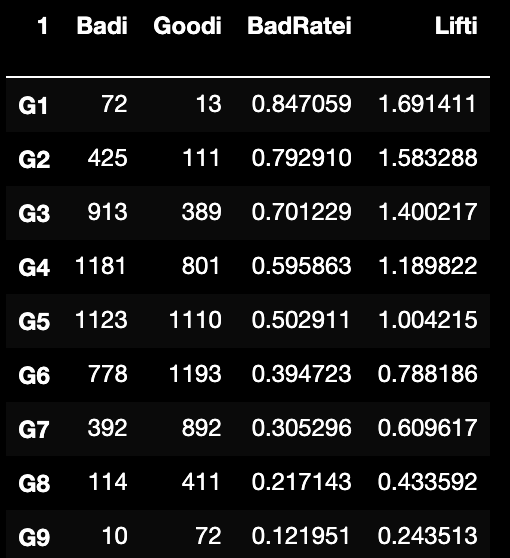
image.png
PS：这里Lift很受整体样本5.5 模型指标 - 图93的影响，假设为0.25那么Lift上限不超过4

5.5.5 模型区分度

区分度即模型对好坏样本的区分能力。在信贷风控中，坏样本分数分布和好样本分布之间的区别越大，则模型对好坏样本的区分能力越强。为了进一步细化区分能力，在此介绍阈值(Cut Off)的概念。一般的，会把模型输出的预测概率如0.625，大于等于阈值0.5则定义预测结果为1，小于阈值0.5则定义预测结果为0，当然这个阈值可以被自定义修改，下面将介绍。

5.5.5.1 ROC曲线

5.5 模型指标 - 图94曲线即5.5 模型指标 - 图95与5.5 模型指标 - 图96之间的关系曲线，其中x轴为5.5 模型指标 - 图97，y轴为5.5 模型指标 - 图98。显然5.5 模型指标 - 图99越高，也就是正样本中分类器预测正确，5.5 模型指标 - 图100越低，也就是负样本中分类器预测错误，这样的模型性能就越好。具体做法为：通过改变不同的阈值5.5 模型指标 - 图101，得到一系列混淆矩阵，进而得到一系列的5.5 模型指标 - 图102和5.5 模型指标 - 图103，绘制出5.5 模型指标 - 图104曲线。
在模型5.5 模型指标 - 图105上，在每0.1一个阈值时可得到 5.5 模型指标 - 图106如下：

  1. 0.0, 1.000000, 1.000000
  2. 0.1, 0.998602, 0.999800
  3. 0.2, 0.952476, 0.991787
  4. 0.3, 0.818890, 0.941707
  5. 0.4, 0.603235, 0.831330
  6. 0.5, 0.370008, 0.635016
  7. 0.6, 0.169928, 0.389824
  8. 0.7, 0.054113, 0.173077
  9. 0.8, 0.009185, 0.044872
  10. 0.9, 0.000399, 0.003205
  11. 1.0, 0.000000, 0.000000

进而得到5.5 模型指标 - 图107曲线：
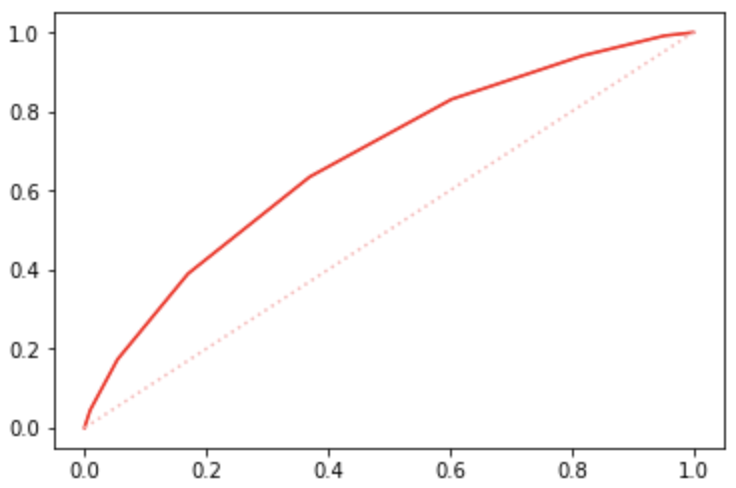
image.png

5.5.5.2 AUC

5.5 模型指标 - 图109值为5.5 模型指标 - 图110曲线与坐标轴围成的区域面积。显然，5.5 模型指标 - 图111越大，则模型分类效果越好。5.5 模型指标 - 图112反映的是分类器对样本的排序能力。从物理意义上来说，

5.5 模型指标 - 图113反映的是好样本的预测结果大于坏样本预测结果的概率

在模型5.5 模型指标 - 图114上，5.5 模型指标 - 图115为0.6841，如下：
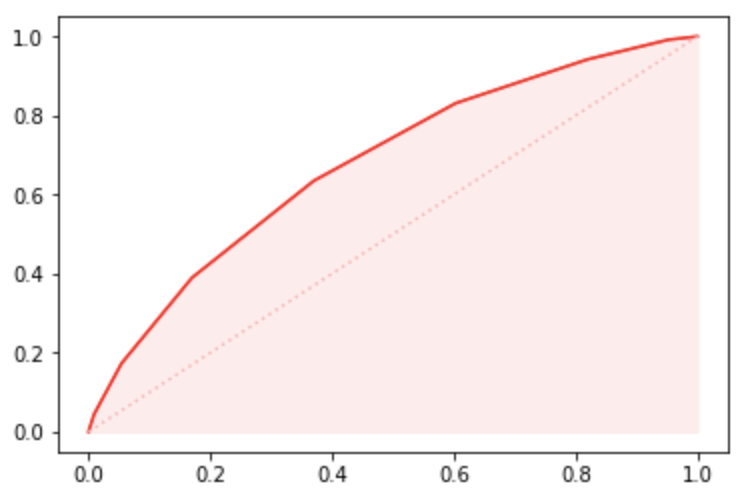
image.png

  • 方法1

    1.   简单的，![](https://g.yuque.com/gr/latex?AUC#card=math&code=AUC&id=gCRM6)既然是![](https://g.yuque.com/gr/latex?ROC#card=math&code=ROC&id=yi4o4)曲线下的面积，面积可拆解为一个个小的梯形面积之和，具体计算的精度与阈值的精度有关。

  • 方法2

    1.   在有![](https://g.yuque.com/gr/latex?n_T#card=math&code=n_T&id=zclrc)个好样本、![](https://g.yuque.com/gr/latex?n_F#card=math&code=n_F&id=IO17I)个坏样本的数据集中，共有![](https://g.yuque.com/gr/latex?n_T%20%5Ccdot%20n_F#card=math&code=n_T%20%5Ccdot%20n_F&id=WmuSM)对好坏样本组，（所谓一对好坏样本，即一个好样本与一个坏样本）。统计这![](https://g.yuque.com/gr/latex?n_T%20%5Ccdot%20n_F#card=math&code=n_T%20%5Ccdot%20n_F&id=E4JtP)对样本里，好样本的预测概率大于坏样本的预测概率的个数。

5.5 模型指标 - 图117)%7D%7Bn_T%20%5Ctimes%20n_F%7D%0A#card=math&code=AUC%20%3D%20%5Cfrac%7B%5Csum%28I%28P_T%20%3E%20P_F%29%29%7D%7Bn_T%20%5Ctimes%20n_F%7D%0A&id=GnLSF)

5.5 模型指标 - 图118#card=math&code=I%28P_T%20%3E%20P_F%29&id=Elozm)可理解为1 if P_T > P_F else 0.

如：

样本 label 预测概率
A 0 0.1
B 0 0.4
C 1 0.35
D 1 0.8

有2个好样本、2个坏样本，共有4对好坏样本组5.5 模型指标 - 图119#card=math&code=%28T%2CF%29&id=bCNKa)，分别是：

5.5 模型指标 - 图120%E3%80%81(C%2CB)%E3%80%81(D%2CA)%E3%80%81(D%2CB)%0A#card=math&code=%28C%2CA%29%E3%80%81%28C%2CB%29%E3%80%81%28D%2CA%29%E3%80%81%28D%2CB%29%0A&id=h6vzO)

那么，

5.5 模型指标 - 图121)%7D%7Bn_T%20%5Ctimes%20n_F%7D%20%5C%5C%0A%26%3D%20%5Cfrac%7BI(P_C%20%3E%20P_A)%20%2B%20I(P_C%20%3E%20P_B)%20%2B%20I(P_D%20%3E%20P_A)%20%2B%20I(P_D%20%3E%20P_B)%7D%7B4%7D%20%5C%5C%0A%26%3D%20%5Cfrac%7BI(0.35%20%3E%200.1)%20%2B%20I(0.35%20%3E%200.4)%20%2B%20I(0.8%20%3E%200.1)%20%2B%20I(0.8%20%3E%200.4)%7D%7B4%7D%20%5C%5C%0A%26%3D%20%5Cfrac%7B1%2B0%2B1%2B1%7D%7B4%7D%20%3D%200.75%5C%5C%0A%5Cend%7Balign%7D%0A#card=math&code=%5Cbegin%7Balign%7D%0AAUC%20%26%3D%20%5Cfrac%7B%5Csum%28I%28P_T%20%3E%20P_F%29%29%7D%7Bn_T%20%5Ctimes%20n_F%7D%20%5C%5C%0A%26%3D%20%5Cfrac%7BI%28P_C%20%3E%20P_A%29%20%2B%20I%28P_C%20%3E%20P_B%29%20%2B%20I%28P_D%20%3E%20P_A%29%20%2B%20I%28P_D%20%3E%20P_B%29%7D%7B4%7D%20%5C%5C%0A%26%3D%20%5Cfrac%7BI%280.35%20%3E%200.1%29%20%2B%20I%280.35%20%3E%200.4%29%20%2B%20I%280.8%20%3E%200.1%29%20%2B%20I%280.8%20%3E%200.4%29%7D%7B4%7D%20%5C%5C%0A%26%3D%20%5Cfrac%7B1%2B0%2B1%2B1%7D%7B4%7D%20%3D%200.75%5C%5C%0A%5Cend%7Balign%7D%0A&id=DDDi5)

  • 方法3

    1.   方法2存在重复计算的缺点，如上例![](https://g.yuque.com/gr/latex?P_C%20%3D%200.5#card=math&code=P_C%20%3D%200.5&id=EBDIc)时，已知![](https://g.yuque.com/gr/latex?I(P_C%20%3E%20P_A)%20%2B%20I(P_C%20%3E%20P_B)%20%3D2#card=math&code=I%28P_C%20%3E%20P_A%29%20%2B%20I%28P_C%20%3E%20P_B%29%20%3D2&id=NoX6v)时，如果![](https://g.yuque.com/gr/latex?P_D%20%5Cge%20P_C#card=math&code=P_D%20%5Cge%20P_C&id=HDmII)，我们甚至都无需理会![](https://g.yuque.com/gr/latex?P_A%E3%80%81P_B%E3%80%81P_D#card=math&code=P_A%E3%80%81P_B%E3%80%81P_D&id=fYOsw)的具体值，就已经知道![](https://g.yuque.com/gr/latex?I(P_D%20%3E%20P_A)%20%2B%20I(P_D%20%3E%20P_B)%20%3D2#card=math&code=I%28P_D%20%3E%20P_A%29%20%2B%20I%28P_D%20%3E%20P_B%29%20%3D2&id=ryOZ8).
    3.   那么，在有![](https://g.yuque.com/gr/latex?n_T#card=math&code=n_T&id=pWAKP)个好样本、![](https://g.yuque.com/gr/latex?n_F#card=math&code=n_F&id=cxro3)个坏样本的数据集中，

（1）对预测概率从高到低排序；

（2）对每一个概率值设一个5.5 模型指标 - 图122值（最高概率5.5 模型指标 - 图123，第二高概率5.5 模型指标 - 图124）；

（3）把好样本的5.5 模型指标 - 图125值求和再减去常数项5.5 模型指标 - 图126%7D%7B2%7D#card=math&code=%5Cfrac%7Bn_T%281%2Bn_T%29%7D%7B2%7D&id=LotSS)（有兴趣可自行推演）；

  1.     这样可以计算复杂度将自![](https://g.yuque.com/gr/latex?O(n_T%20%5Ccdot%20n_F)#card=math&code=O%28n_T%20%5Ccdot%20n_F%29&id=Odows)降至![](https://g.yuque.com/gr/latex?O(n_T%2Bn_F)#card=math&code=O%28n_T%2Bn_F%29&id=wWgUv)，得到：

5.5 模型指标 - 图127%7D%7B2%7D%2B%5Csum_i%7Brank_i%7CT%7D%7D%7Bn_T%20%5Ctimes%20n_F%7D%20%5C%5C%0A%26%3D%20%5Cfrac%7B-%5Cfrac%7B2(1%2B2)%7D%7B2%7D%2B(4%2B2)%7D%7B4%7D%20%3D%20%5Cfrac%7B-3%2B6%7D%7B4%7D%20%3D%200.75%0A%5Cend%7Balign%7D%0A#card=math&code=%5Cbegin%7Balign%7D%0AAUC%20%26%3D%20%5Cfrac%7B-%5Cfrac%7Bn_T%281%2Bn_T%29%7D%7B2%7D%2B%5Csum_i%7Brank_i%7CT%7D%7D%7Bn_T%20%5Ctimes%20n_F%7D%20%5C%5C%0A%26%3D%20%5Cfrac%7B-%5Cfrac%7B2%281%2B2%29%7D%7B2%7D%2B%284%2B2%29%7D%7B4%7D%20%3D%20%5Cfrac%7B-3%2B6%7D%7B4%7D%20%3D%200.75%0A%5Cend%7Balign%7D%0A&id=xUMLZ)

  1.     一般认定，

5.5 模型指标 - 图128

5.5.5.3 洛伦兹曲线

洛伦兹曲线最先用来描述社会收入不均衡的现象，在一个总体（国家、地区）内，以“最贫穷的人口计算起一直到最富有人口”的人口百分比对应各个人口百分比的收入百分比的点组成的曲线。为了研究国民收入在国民之间的分配问题，统计学家 M.O.洛伦兹提出了著名的洛伦兹曲线。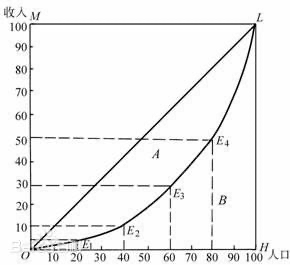
image.png

首先将全社会的人按照收入升序排序，然后计算累计前5.5 模型指标 - 图130的人的收入占社会总收入的百分之几，这个数值就是对应5.5 模型指标 - 图131的5.5 模型指标 - 图132，洛伦兹曲线就是这一函数的图像。例如：假设收入最低的前1%的人其收入占比为1%，前2%的人收入占比为2%……前99%的人收入占比为99%，那么洛伦兹曲线就与收入分配绝对平等直线重合，此时全社会所有人的收入都是一样的。再如：假设收入最低的前99%的人其收入占比为50%，那就意味着剩下1%的人拿走了全社会50%的收入，此时洛伦兹曲线严重偏离收入分配绝对平等直线。显然，社会收入越平均，洛伦兹曲线越接近收入分配绝对平等直线。
将其引入模型领域，计算步骤：
（1）计算各分组内的好坏账户数；
（2）计算各分组内的累计好账户数占总好账户数比率、累计坏账户数占总坏账户数比率；
（3）按照累计好账户占比和累计坏账户占比得出洛伦兹曲线；
在模型5.5 模型指标 - 图133上，在每一个评分分组可得到 5.5 模型指标 - 图134如下：

  1. G1, 0.014377, 0.002604
  2. G2, 0.099241, 0.024840
  3. G3, 0.281550, 0.102764
  4. G4, 0.517372, 0.263221
  5. G5, 0.741613, 0.485577
  6. G6, 0.896965, 0.724559
  7. G7, 0.975240, 0.903245
  8. G8, 0.998003, 0.985577
  9. G9, 1.000000, 1.000000

进而得到洛伦兹曲线：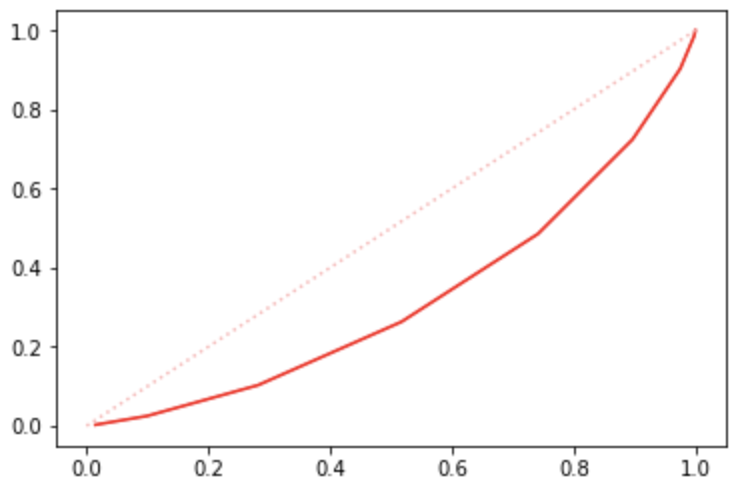
image.png

5.5.5.4 Gini

5.5 模型指标 - 图136系数是指绝对公平线和洛伦兹曲线围成的面积与绝对公平线以下面积的比例。
在模型5.5 模型指标 - 图137上，
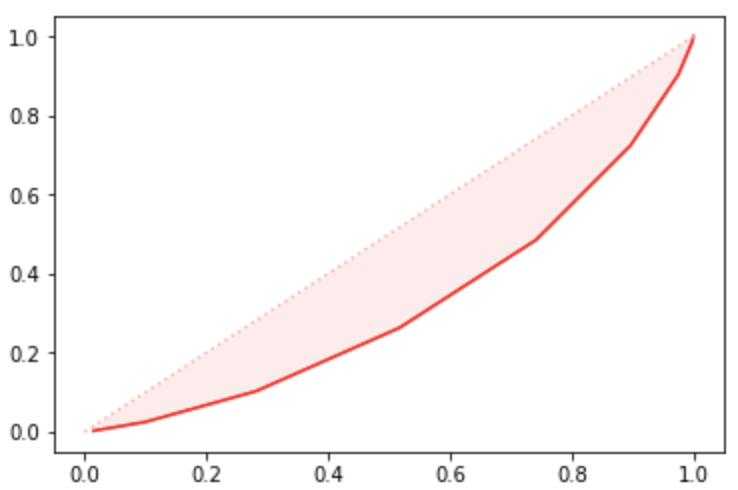
image.png
推演逻辑可参考AUC计算。

5.5.5.5 KS

5.5 模型指标 - 图139(Kolmogorov-Smirnov)用于模型风险区分能力进行评估，指标衡量的是好坏样本累计分部之间的差值。好坏样本累计差异越大，5.5 模型指标 - 图140指标越大，那么模型的风险区分能力越强。
计算步骤：
（1）计算各分组内的好坏账户数；
（2）计算各分组内的累计好账户数占总好账户数比率、累计坏账户数占总坏账户数比率；
（3）计算各分组内的累计坏账户占比与累计好账户占比差的绝对值，然后对这些绝对值取最大值即KS值；

5.5 模型指标 - 图141)%0A#card=math&code=KS%20%3D%20max%28abs%28%5Cfrac%7BCumBad_i%7D%7BSumBab_i%7D%20-%20%5Cfrac%7BCumBad_i%7D%7BSumBab_i%7D%29%29%0A&id=C8WjR)
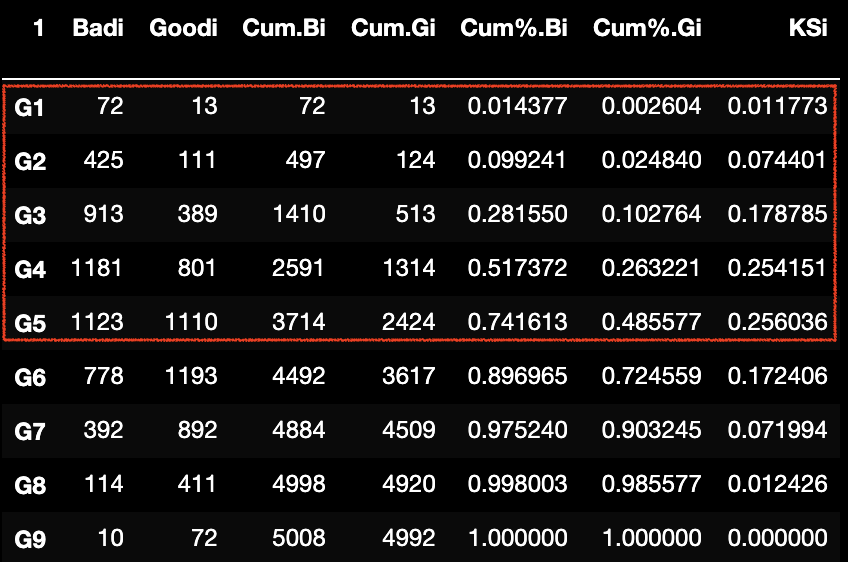
image.png
在模型5.5 模型指标 - 图143上，5.5 模型指标 - 图144为0.2560，
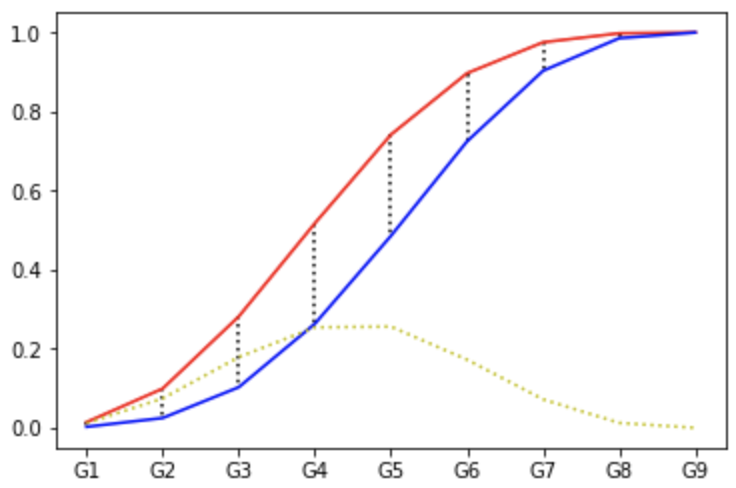
image.png
这里，我们可以做这样的理解，当模型5.5 模型指标 - 图146选择拒绝5.5 模型指标 - 图147所在组5.5 模型指标 - 图148以及评分分组以下时，在拒绝74.16%坏样本作为“收益”的同时，也付出了错误拒绝48.56%好样本的“代价”。那么5.5 模型指标 - 图149就是在体现这种收益与代价差距的最大化。如果可能的话，我们希望5.5 模型指标 - 图150是64%，那么在拒绝相同的74.16%坏样本作为“收益”时，仅付出错误拒绝10.16%好样本的“代价”。

  1.     一般认定，

5.5 模型指标 - 图151

5.5.6 模型稳定性

模型稳定性指标：5.5 模型指标 - 图152、5.5 模型指标 - 图153，如下。

5.5.6.1 PSI

5.5 模型指标 - 图154指标是指群体稳定性指数（Population Stability Index），5.5 模型指标 - 图155反映了不同样本在各分数段的分布的稳定性。
计算公式：

5.5 模型指标 - 图156%20%5Ctimes%20%5Cln(Ai%2FE_i)%0A#card=math&code=PSI%20%3D%20%5Csum%7Bi%3D1%7D%5En%20%28A_i%20-%20E_i%29%20%5Ctimes%20%5Cln%28A_i%2FE_i%29%0A&id=z96r9)
其中，5.5 模型指标 - 图157表示实际Actual样本，5.5 模型指标 - 图158表示预期Excepted样本。
一般认定，

5.5 模型指标 - 图159

如下示例：

序号 Score 5.5 模型指标 - 图160 5.5 模型指标 - 图161 5.5 模型指标 - 图162 5.5 模型指标 - 图163#card=math&code=%5Cln%28A_i%2FE_i%29&id=Bmnu9) 5.5 模型指标 - 图164 5.5 模型指标 - 图165
1 (500, 550] 12.0% 5.0% 2.4 0.88 7.0% 0.061
2 (550, 600] 15.0% 8.0% 1.875 0.63 7.0% 0.044
3 (600, 650] 33.0% 30.0% 1.1 0.10 3.0% 0.003
4 (650, 700] 18.0% 25.0% 0.72 -0.33 -7.0% 0.023
5 (700, 750] 12.0% 14.0% 0.857 -0.15 -2.0% 0.003
6 (750, 800] 8.0% 10.0% 0.8 -0.22 -2.0% 0.004
7 (800, 850] 1.0% 5.0% 0.2 -1.61 -4.0% 0.064
8 (850, 900] 1.0% 2.0% 0.5 -0.69 -1.0% 0.007
9 (900, 950] 0.0% 1.0% 0.01 -4.61 -1.0% 0.046
10 (950, 1000] 0.0% 0.0% / 0.00 0.0% 0.000
5.5 模型指标 - 图166 0.256

5.5.6.2 CSI

5.5 模型指标 - 图167指标是指特定稳定性指数（Characteristic Stability Index），用来衡量样本在特征层面上的分布变化，反映了特征对评分卡分数变化的影响。当评分卡主模型分数发生变化时，对每个特征计算5.5 模型指标 - 图168I，可以知道哪些特征分布发生变化从而导致的评分卡主模型分数偏移以及哪个特征对模型得分变化的影响最大。
计算公式：

5.5 模型指标 - 图169%20Scorei%0A#card=math&code=CSI%20%3D%20%5Csum%7Bi%3D1%7D%5En%20%28A_i%20-%20E_i%29%20Score_i%0A&id=qaA6g)

其中，5.5 模型指标 - 图170表示实际Actual样本，5.5 模型指标 - 图171表示预期Excepted样本，Score表示分箱分值。

序号 Score 5.5 模型指标 - 图172 5.5 模型指标 - 图173 5.5 模型指标 - 图174 5.5 模型指标 - 图175 5.5 模型指标 - 图176 5.5 模型指标 - 图177
1 (0, 0.5] 21.1% 24.4% 0.865 17 -3.3% -0.561
2 (0.5, 1.2] 24.0% 24.5% 0.980 19 -0.5% -0.095
3 (1.2, 3.1] 16.2% 15.7% 1.038 26 0.5% 0.13
4 (3.1, 6.0] 21.1% 16.9% 1.249 30 4.2% 1.26
5 (6.0, +) 17.4% 18.4% 0.946 40 -1.0% -0.40
5.5 模型指标 - 图178 0.334

5.5.7 代码摘要

以下摘要上述推演过程的Python代码：

  1. import pandas as pd
  2. from sklearn.metrics import *
  3. import matplotlib.pyplot as plt
  4. from sklearn.datasets import make_classification
  5. from sklearn.linear_model import LogisticRegression
  7. X, Y = make_classification(
  8.     n_samples=10000, 
  9.     n_features=1000, 
  10.     n_informative=5, 
  11.     n_redundant=5, 
  12.     flip_y=1)
  13. model = LogisticRegression()
  14. model.fit(X, Y)
  15. #
  16. print(X.shape, Y.shape)
  17. print(pd.value_counts(Y)/pd.value_counts(Y).sum())
  18. print(pd.value_counts(Y))
  20. #
  21. print(
  22.     "%.4f" % accuracy_score(model.predict(X), Y),
  23.     "%.4f" % f1_score(model.predict(X), Y),
  24.     "%.4f" % precision_score(model.predict(X), Y),
  25.     "%.4f" % recall_score(model.predict(X), Y)
  26. )
  27. fpr, tpr, thresholds = roc_curve(Y, model.predict_proba(X)[:,1], pos_label=1)
  28. print("AUC: %.4f" % auc(fpr, tpr))
  30. #
  31. vBadRate = pd.value_counts(Y)[0]/pd.value_counts(Y).sum()
  32. print(vBadRate)
  34. #
  35. print(pd.crosstab(model.predict(X), Y))
  37. #
  38. data = pd.DataFrame([
  39.     f"G{int(round(_, 1)*10)}" 
  40.     for _ in model.predict_proba(X)[:,1]]
  41. )
  42. data[1] = Y
  43. _rb = pd.crosstab(data[0], data[1])
  44. _rb.index.name = ""
  45. _rb.rename_axis({0:"Badi", 1:"Goodi"}, inplace=True, axis=1)
  46. print(_rb)
  48. #
  49. _r = _rb.copy()
  50. _r["Sumi"] = _r["Badi"] + _r["Goodi"]
  51. _r["BadRatei"] = _r["Badi"]/_r["Sumi"]
  52. print(_r)
  54. #
  55. _r = _rb.copy()
  56. _r["Oddsi"] = _r["Badi"]/_r["Goodi"]
  57. print(_r)
  59. #
  60. _r = _rb.copy()
  61. _r["BadRatei"] = _r["Badi"]/(_r["Badi"]+_r["Goodi"])
  62. _r["Lifti"] = _r["BadRatei"]/vBadRate
  63. print(_r)
  65. #
  66. _r = _rb.copy()
  67. _ = 0
  68. def f(i):
  69.     global _
  70.     _ += i
  71.     return _
  72. _r["Cum.Bi"] = _r["Badi"].apply(f)
  73. _ = 0
  74. def f(i):
  75.     global _
  76.     _ += i
  77.     return _
  78. _r["Cum.Gi"] = _r["Goodi"].apply(f)
  79. print(max(_r["Cum.Bi"]), max(_r["Cum.Gi"]))
  80. _r["Cum%.Bi"] = _r["Cum.Bi"]/max(_r["Cum.Bi"])
  81. _r["Cum%.Gi"] = _r["Cum.Gi"]/max(_r["Cum.Gi"])
  82. _r["KSi"] = _r["Cum%.Bi"] - _r["Cum%.Gi"]
  83. _r["KSi"] = [abs(_) for _ in _r["KSi"]]
  84. print(_r)
  86. #
  87. plt.plot(_r.index, _r["Cum%.Bi"], color="r")
  88. plt.plot(_r.index, _r["Cum%.Gi"], color="b")
  89. plt.plot(_r.index, _r["Cum%.Bi"]-_r["Cum%.Gi"], color="y", linestyle=":")
  90. for i, j1, j2 in zip(_r.index, _r["Cum%.Bi"], _r["Cum%.Gi"]):
  91.     plt.vlines(i, ymin=j1, ymax=j2, colors="k", linestyle=":")
  92. plt.show()
  94. #
  95. print(_r[["Cum%.Bi", "Cum%.Gi"]])
  96. plt.plot(_r["Cum%.Bi"], _r["Cum%.Gi"], color="r")
  97. plt.plot([0, 1.0], [0, 1.0], color="#FFB5B5", linestyle=":")
  98. plt.fill_between(
  99.     [_ for _ in _r["Cum%.Bi"]], [_ for _ in _r["Cum%.Gi"]], [_ for _ in _r["Cum%.Bi"]], 
  100.     color="#FFECEC"
  101. )
  102. plt.show()
  104. #
  105. print(_r[["Cum%.Bi", "Cum%.Gi"]])
  106. plt.plot(_r["Cum%.Bi"], _r["Cum%.Gi"], color="r")
  107. plt.plot([0, 1.0], [0, 1.0], color="#FFB5B5", linestyle=":")
  108. plt.show()
  110. #
  111. data = pd.DataFrame(model.predict_proba(X)[:,1])
  112. data[1] = Y
  113. _rP1, _rP2 = [], []
  114. for icut in range(0, 101, 10):
  115.     try:
  116.         icut = icut/100
  117.         data[2] = [1 if _ >= icut else 0 for _ in data[0]]
  118.         _rC = pd.crosstab(data[2], data[1])
  119.         TN, FP, FN, TP = _rC[0][0], _rC[0][1], _rC[1][0], _rC[1][1]
  120.         FPR = FP/(FP + TN)
  121.         TPR = TP/(TP + FN)
  122.         _rP1.append([FPR, TPR])
  123.         _rP2.append([icut, icut])
  124.     except:
  125.         FPR, TPR = 1-icut, 1-icut
  126.         _rP1.append([FPR, TPR])
  127.         _rP2.append([icut, icut])
  128.     print("%.1f, %.6f, %.6f" % (icut, FPR, TPR))
  129. plt.plot([_[0] for _ in _rP1], [_[1] for _ in _rP1], color="r")
  130. plt.plot([_[0] for _ in _rP2], [_[1] for _ in _rP2], color="#FFB5B5", linestyle=":")
  131. plt.show()
  133. #
  134. data = pd.DataFrame(model.predict_proba(X)[:,1])
  135. data[1] = Y
  136. _rP1, _rP2 = [], []
  137. for icut in range(0, 101, 10):
  138.     try:
  139.         icut = icut/100
  140.         data[2] = [1 if _ >= icut else 0 for _ in data[0]]
  141.         _rC = pd.crosstab(data[2], data[1])
  142.         TN, FP, FN, TP = _rC[0][0], _rC[0][1], _rC[1][0], _rC[1][1]
  143.         FPR = FP/(FP + TN)
  144.         TPR = TP/(TP + FN)
  145.         _rP1.append([FPR, TPR])
  146.         _rP2.append([icut, icut])
  147.     except:
  148.         FPR, TPR = 1-icut, 1-icut
  149.         _rP1.append([FPR, TPR])
  150.         _rP2.append([icut, icut])
  151.     print("%.2f, %.6f, %.6f" % (icut, FPR, TPR))
  152. plt.plot([_[0] for _ in _rP1], [_[1] for _ in _rP1], color="r")
  153. plt.plot([_[0] for _ in _rP2], [_[1] for _ in _rP2], color="#FFB5B5", linestyle=":")
  154. plt.fill_between(
  155.   [_[0] for _ in _rP1], [_[1] for _ in _rP1], [0 for _ in _rP1], 
  156.   color="#FFECEC")
  157. plt.show()