0.2.1 统计学透视

统计学的基本理论是关于如何处理数据人员通常不需担心的数据约束问题。
这些约束中最重要的是样本量。面对大数据，核心任务就是找出解析它的正确方法，一旦完成了从大量数据中提取特征的工作，抽取深层信息就像查看直方图一样简单。
但事实情况并非总是如此。统计学是关于处理这些极其有限的情况，在这种情况下很难判断观察到的模式究竟是事实的真相还是数据的例外。由于分析结果事关巨额财富甚至生命健康，所以统计学往往对每一个细节都非常挑剔。
但往往可能犯下的最严重错误之一就是在需要更严格方法的情况下病危采取措施，故而需要对应急方法的使用范围保持敏感。如果能够在发生这些问题之前学会发现这些缺陷，即可随时学习所需的统计学知识。

0.2.2 贝叶斯与概率论

贝叶斯统计和频率统计（经典统计）在统计学上有巨大分歧，尽管这些差异多是哲学范畴的，在大多数问题中，它们会给出几乎相同的答案。

  • 经典统计

在这里，模型应该是数据的“最佳拟合”。为了解决问题，有必要对模型的形式作出一些假设，然而在其他方面，将模型参数设置为与数据最匹配。经典统计学中最重要的范例是询问为数据给出的特定模型或特定的一组参数的合理程度，并设定参数以使数据尽可能合理。如果必须进行统计预测，那么则使用这个拟合效果最好的模型。

  • 贝叶斯统计

贝叶斯模型以所谓“先验”开始，它存在于没有任何数据的情况下。随着数据的出现，改进了置信分布，希望能够调整真实世界的“真实”参数。即人们不仅仅拥有真实世界模型的最佳拟合参数，而且对这些最适合的参数可能会有一个置信度分布。

0.2.3 假设检验

统计学的一个重要领域称为假设检验。基本的想法是，思考数据的趋势，评估它称为现实世界现象的可能性。假设检验不能解决趋势有多强的问题。它的设计适用于数据过于稀疏而无法可靠地量化趋势的情况。
假设检验的一个典型例子是这样的：有一个可能公平或不公平的硬币，扔了10次，得到9次正面。那么这枚硬币被动手脚的可能性有多大？
为了回答这个问题，可以首先假设硬币是公平的，从而计算这个偏斜数据的可能性，并用它来衡量这个硬币是否是公平的，以下计算能得到9/10个正背面概率：
0.2 统计学 - 图2*2%2F2%5E%7B10%7D%3D22%2F1024%3D0.0215%0A#card=math&code=%281%2B10-1%29%2A2%2F2%5E%7B10%7D%3D22%2F1024%3D0.0215%0A&id=mibDw)
所以只有2%的机会从公平的硬币中得到类似这样的数据，我们倾向认为硬币是不公平的。
这里公平硬币的概念被称为“零假设”，如果将零假设作为给定数据，那么可能会看到数据中极端的模式，这个数字被称为0.2 统计学 - 图3值。如果0.2 统计学 - 图4值低于某个指定的阈值（通常使用0.05），则结果称为统计显著性。

关于假设检验需要特别注意的是，它只是告诉人们存在一种模式，但并不告诉人们该模式实际有多强。毕竟抛硬币1百万次，我们就会发现它是否公平。在大数据情况下，如果模式足够弱，甚至不得不诉诸0.2 统计学 - 图5值，那么该模式肯定太弱，而无法具有任何商业价值。

0.2.4 多重假设检验

在多重假设检验中，我们知道需要对错误率进行控制，因为小概率事件在一次试验中不会发生。比如我们经常把显著性水平0.2 统计学 - 图6设为0.05，也就是说，我们认为概率小于0.05的事件在一次试验中不会发生。但如果我们试验非常多次，那么小概率事件就极有可能发生了，所以在多重假设检验中，我们如果仍然把显著性水平设为0.05，那么假阳性（错误测试）事件会大大增多。
因为P值的阈值是人为规定的，无论是多小的P值，也仅仅能代表结果的低假阳性，而非保证结果为真。即使P值已经很小（比如0.05），也会被检验的总次数无限放大。比如检验10000次，得到假阳性结果的次数就会达到 5%0.2 统计学 - 图710000=500次。
这时候我们就需要引入多重检验来进行校正，从而减低假阳性结果在我们的检验中出现的次数。

  • 0.2 统计学 - 图8校正

    0.2 统计学 - 图9校正法可以称作是“最简单粗暴有效”的校正方法，它拒绝了所有的假阳性结果发生的可能性，通过对p值的阈值进行校正来实现消除假阳性结果。
    0.2 统计学 - 图10校正的公式为0.2 统计学 - 图11#card=math&code=p%5Ctimes%20%281%2Fn%29&id=DRKXb)，其中0.2 统计学 - 图12为原始阈值，0.2 统计学 - 图13为总检验次数。
    如果像我们举的例子一样，原始的P值为0.05，检验次数为10000次，那么在0.2 统计学 - 图14校正中，校正的阈值就等于5%/10000 = 0.000005，所有P值超过0.00005的结果都被认为是不可靠的。这样的话假阳性结果在10000次检验中出现的次数为0.0000050.2 统计学 - 图15 10000=0.5，还不到1次。
    但是这也存在问题：0.2 统计学 - 图16 太过严格，被校正后的阈值拒绝的不只有假阳性结果，很多阳性结果也会被它拒绝。

  • FDR(FalseDiscovery Rate)校正

相对而言FDR温和得多，这种校正方法不追求完全没有假阳性结果，而是将假阳性结果和真阳性的比例控制在一定范围内。
举个例子，我们最开始设定的情况中进行了10000次检验，这次我们设定FDR<0.05，如果我们的检验对象为差异表达的基因，那么在10000次检验中假如得到了500个基因，那么这500个基因中的假阳性结果小于 500![](https://cdn.nlark.com/yuque/__latex/60c13e05d3ec8c10b8564eae7023d9db.svg#card=math&code=%5Ctimes&height=11&id=T02Z2)5% = 25 个。
具体的，BH-Benjaminiand Hochberg法将总计0.2 统计学 - 图17次检验的结果按由小到大进行排序，0.2 统计学 - 图18为其中一次检验结果的0.2 统计学 - 图19值所对应的排名。找到符合原始阈值0.2 统计学 - 图20的最大的0.2 统计学 - 图21值，满足0.2 统计学 - 图22%20%5Cle%20%5Calpha%20k%2Fm#card=math&code=p%28k%29%20%5Cle%20%5Calpha%20k%2Fm&id=Usb7W)，认为排名从1到0.2 统计学 - 图23的所有检验存在显著差异，并计算对应的0.2 统计学 - 图24值公式为0.2 统计学 - 图25#card=math&code=q%20%3D%20p%20%5Ctimes%20%28m%2Fk%29&id=KBUwZ)。

0.2.5 参数估计

假设检验是用来判定效果是否存在，而不是量化其大小。后者属于参数估计的范畴，即对表征分布的基本参数进行估计。
在参数估计中，假设数据服从某些函数形式，例如具有平均值0.2 统计学 - 图26和标准差0.2 统计学 - 图27的正态分布。然后有一些方法来估计这些参数，给出以下数据：
0.2 统计学 - 图28%5E2%7D%20%5C%5C%0A#card=math&code=%5Chat%20%5Cmu%20%3D%20%5Cfrac%7B1%7D%7BN%7D%5Csum%7Bi%3D1%7D%5E%7BN%7D%20x_i%20%5C%5C%0A%5Chat%20%5Csigma%20%3D%20%5Csqrt%7B%5Cfrac%7B1%7D%7BN%7D%20%5Csum%7Bi%3D1%7D%5E%7BN%7D%28x_i%20-%20%5Chat%20%5Cmu%29%5E2%7D%20%5C%5C%0A&id=uktbM)
在这种情况下，这些数字称为样本均值和样本方差。
这样有术语：

  • 一致性：在数据集中包含很多不同的数据点的条件下，估计量0.2 统计学 - 图29收敛到实数0.2 统计学 - 图30，那么这个估计量0.2 统计学 - 图31是一致的。
  • 偏差：如果0.2 统计学 - 图32的期望值是实数0.2 统计学 - 图33，则该估计量是无偏的。

标准差的无偏估计量是
0.2 统计学 - 图34%5E2%7D%0A#card=math&code=%5Chat%20%5Csigma%20%3D%20%5Csqrt%7B%5Cfrac%7B1%7D%7BN-1%7D%20%5Csum_%7Bi%3D1%7D%5E%7BN%7D%28x_i%20-%20%5Chat%20%5Cmu%29%5E2%7D%0A&id=DEPde)
这总会比原是表达式稍微大些，但是随着0.2 统计学 - 图35趋于无穷，它们会收敛到同一个数值。

0.2.6 假设检验：0.2 统计学 - 图36检验

  1. ![](https://g.yuque.com/gr/latex?t#card=math&code=t&id=AKcMo)检验是假设检验的更复杂版本。当需要测量的是一个连续的数字，而不是二元的硬币翻转，并且想评估两个分布的真实平均值是否相同时，它是有用的。例如，如果对曾服用或未服用降血压药物的患者进行血压测量，是否能够自信地宣称其有效性？<br />这次先模拟之：
  1. from scipy.stats import ttest_ind
  2. t_score, p_value = ttest_ind([1, 2, 3, 4], [2, 2.2, 3, 5])
  3. print(t_score, p_value)
  5. t_score, p_value = ttest_ind([1, 2, 3, 4], [2, 2.2, 3, 5], equal_var=False)
  6. print(t_score, p_value)
  7. """
  8. -0.5843683421954862 0.580264402955629
  9. -0.5843683421954862 0.5803365979495375
  10. """

再回顾下假设检验过程，设定零假设，选择一个检验统计量来获取发现的模式的强度，然后计算检验统计量为异常值的可能性大小。如果检验统计量非常大，则零假设可能为假。
0.2 统计学 - 图37检验给出了零假设的两个选择：

  • 两个数据集来自相同的正态分布；
  • 服从正态分布的两个数据集，但标准差可能不同；

重要的一点是，这些假设并没有给出一个概率分布。这与硬币翻转形成对比，通过假设硬币是公平的即可获得抛掷的概率分布。在0.2 统计学 - 图38检验中，会对一些无法计算的事件产生兴趣，因为这些事件由那些无法指定的参数所决定。
在设定检验统计量量，需要遵循如下规则：

  • 计算两个数据集的平均值0.2 统计学 - 图39和0.2 统计学 - 图40，并观察它们之间的距离；
  • 如果数据集中有更多的点，期望0.2 统计学 - 图41和0.2 统计学 - 图42更接近真实的和。在这种情况下，如果零假设为真，那么0.2 统计学 - 图43和0.2 统计学 - 图44之间的差异应该很小；
  • 如果数据集本身具有很大的方差，则0.2 统计学 - 图45和0.2 统计学 - 图46会是真实和的更差近似值，所以0.2 统计学 - 图47和0.2 统计学 - 图48可能会更大；

即0.2 统计学 - 图49统计量：
0.2 统计学 - 图50
式中，0.2 统计学 - 图51、0.2 统计学 - 图52分别是0.2 统计学 - 图53和0.2 统计学 - 图54的样本方差。
如果零假设为真，则0.2 统计学 - 图55将遵循所谓的0.2 统计学 - 图56分布。0.2 统计学 - 图57分布看起来非常像均值为0、标准差为1的正态分布，但尾部较厚。如果数据的0.2 统计学 - 图58统计量特别大或特别小，那么零假设可能为假。

0.2.7 置信区间

当试图从数据中估计真实世界分布的参数时，通常还需要给出置信区间，而不只是一个最佳拟合数。置信区间最常见的用途是计算基本分布的平均值。如果需要计算其他信息，则可以通过分析数据，将其转换为关于平均值的计算。
置信区间最常见的用途是计算基本分布的平均值。如果需要计算其他信息，则可以通过分析数据，将其转换为关于平均值的计算。例如，如果想估计随机变量0.2 统计学 - 图59的标准差。那么，可以发现如下关系：
0.2 统计学 - 图60%5E2%5D%7D%20%5C%5C%0A%5Csigma_x%5E2%20%3D%20E%5B(X%20-%20E%5BX%5D)%5E2%5D%20%5C%5C%0A#card=math&code=%5Csigma_x%20%3D%20%5Csqrt%7BE%5B%28X%20-%20E%5BX%5D%29%5E2%5D%7D%20%5C%5C%0A%5Csigma_x%5E2%20%3D%20E%5B%28X%20-%20E%5BX%5D%29%5E2%5D%20%5C%5C%0A&id=SRs29)
因此可以通过找到均值并取二次方根来估计0.2 统计学 - 图61的标准差0.2 统计学 - 图62%5E2#card=math&code=%28X-E%5BX%5D%29%5E2&id=pqVNl)。如果可以将置信区间用于均值，则也可以将置信区间用于一系列拟估计的其他量。典型指标是“平均值的标准误差SEM”，如果看到0.2 统计学 - 图63的平均值，那么通常4.1是通过平均所有数字得到的最佳拟合均值，而0.2是0.2 统计学 - 图64。

  1. from scipy.stats import sem
  2. sed_err = sem([1, 2, 1, 1])
  3. print(sed_err)
  4. """
  5. 0.25
  6. """

如果0.2 统计学 - 图65是样本均值，那么间隔
0.2 统计学 - 图66
将以95%、99%或者任何其他置信度阈值包含均值，这取决于如何设置系数0.2 统计学 - 图67。增加这个系数即可增加置信度。

置信度（%） 系数
99 2.58
95 1.96
90 1.64

“均值以95%的置信度在给定的区间内”不一定对，毕竟真正的均值是否在给定的区间内，更严谨的解释是，如果分布是正态的，并且从0.2 统计学 - 图68个样本中计算出置信区间，则该置信区间将以95%的置信度包含真实均值。

0.2.8 ⻉叶斯统计学

与经典统计类似，贝叶斯统计学假定世界的某些方面遵循具有一些参数的统计模型：类似于正面概率为0.2 统计学 - 图69的硬币。经典统计学选择最拟合数据的参数值（也可以添加置信区间），不能人工干预。在贝叶斯统计学中，从参数的所有可能值的概率分布开始，表示对每个值是“正确”的置信度。随着新的数据点加入，随即更新置信度。从某个意义上说，贝叶斯统计学是一种如何根据数据来完善猜测的科学。
贝叶斯统计学的数据基础是贝叶斯定理。对于任何随机变量0.2 统计学 - 图70和0.2 统计学 - 图71，其公式如下：
0.2 统计学 - 图72%20%3D%20%5Cfrac%7BP(T)P(D%7CT)%7D%7BP(D)%7D%0A#card=math&code=P%28T%7CD%29%20%3D%20%5Cfrac%7BP%28T%29P%28D%7CT%29%7D%7BP%28D%29%7D%0A&id=hHvuy)
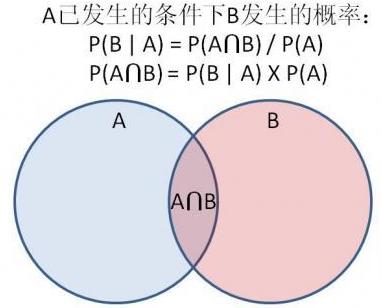
3ac79f3df8dcd100658117d6788b4710b9122f2c.jpeg
举例，问：现分别有 A、B 两个容器，在容器 A 里分别有 7 个红球和 3 个白球，在容器 B 里有 1 个红球和 9 个白球，现已知从这两个容器里任意抽出了一个红球，问这个球来自容器 A 的概率是多少？
答：假设选中容器 A 为事件 A，已经抽出红球为事件 B，B｜A即容器A中抽出红球，则有：
0.2 统计学 - 图74%20%3D%20(7%2B3)%2F(7%2B3%2B1%2B9)%3D0.5%20%5C%5C%0AP(B)%20%3D%20(7%2B1)%2F(7%2B3%2B1%2B9)%3D0.4%20%5C%5C%0AP(B%7CA)%20%3D%207%2F(7%2B3)%20%3D%200.7%20%5C%5C%0A#card=math&code=P%28A%29%20%3D%20%287%2B3%29%2F%287%2B3%2B1%2B9%29%3D0.5%20%5C%5C%0AP%28B%29%20%3D%20%287%2B1%29%2F%287%2B3%2B1%2B9%29%3D0.4%20%5C%5C%0AP%28B%7CA%29%20%3D%207%2F%287%2B3%29%20%3D%200.7%20%5C%5C%0A&id=mwtCG)
按照公式，则有：
0.2 统计学 - 图75%20%3D%20%5Cfrac%7BP(A)P(B%7CA)%7D%7BP(B)%7D%20%3D%200.7%20%5Ctimes%200.5%20%2F%200.4%20%3D%200.875%0A#card=math&code=P%28A%7CB%29%20%3D%20%5Cfrac%7BP%28A%29P%28B%7CA%29%7D%7BP%28B%29%7D%20%3D%200.7%20%5Ctimes%200.5%20%2F%200.4%20%3D%200.875%0A&id=R3Bks)

贝叶斯定理给出了经典统计学中所不具备的东西：给定收集的数据，真实参数等于某个特定值的“概率”。

0.2.9 朴素⻉叶斯统计学

贝叶斯统计中最棘手的部分通常是计算0.2 统计学 - 图76#card=math&code=P%28D%7CT%29&id=fJ6ey)。这主要是因为0.2 统计学 - 图77本身通常是一个多部分随机变量，通常是一个0.2 统计学 - 图78维向量，并且其中的不同数字可能具有非常复杂的依赖结构。例如，如果想知道是否有人患有糖尿病，可能会测量他们的血糖和糖水平，而这两个数字有复杂的依赖关系，需要深入了解生物学模型。或者如果模型必须自动学习这些关系，则需要大量的实验数据，因为必须查看所有共现事件。
由于这个原因，会经常看到人们使用“朴素贝叶斯”方法。在朴素贝叶斯方法中，简单地假设所有不同的变量都以0.2 统计学 - 图79为条件相互独立，即：
0.2 统计学 - 图80%20%3D%20P(D_1%EF%BD%9CT)%20%5Ctimes%20P(D_2%EF%BD%9CT)%20%5Ctimes%20…%20%5Ctimes%20P(D_d%EF%BD%9CT)%0A#card=math&code=P%28D%EF%BD%9CT%29%20%3D%20P%28D_1%EF%BD%9CT%29%20%5Ctimes%20P%28D_2%EF%BD%9CT%29%20%5Ctimes%20…%20%5Ctimes%20P%28D_d%EF%BD%9CT%29%0A&id=Q8Nyd)
现在计算0.2 统计学 - 图81#card=math&code=P%28D%7CT%29&id=o36nb)只需要用已经观察到的足够数据来描述每个变量与0.2 统计学 - 图82的关系。
朴素贝叶斯假设是数据科学领域中最戏剧性、最细微的过度简化之一，但在实践中非常有效。它倾向于做的主要事情是，如果几个密切相关，它们将集体分类推向某一个方向。例如假设试图确定某人的性别，然后可能会告诉读者，他们长发，他们使用发带，并且他们的头发需要很长时间才能晾干。这些事实中的每一个都适度地支持性别为女性的可能性，所以朴素贝叶斯分类器的置信度将会变得非常高。但实际上，这些事实只是一些描述这个人头发长的替代方式，而且还有很多长头发的男性。所以分类器可能是对的，但是会具有过高的置信度。

0.2.A 贝叶斯网络

如果数据中有很多特征，完全拟合0.2 统计学 - 图83#card=math&code=P%28D%7CT%29&id=C4x8b)的模型是不现实的，因为变量之间存在所有可能的相关性。然而在这个不可能的任务和朴素贝叶斯过度简化中，存在一种折中办法， 被称为贝叶斯网络。
在实际应用中使用贝叶斯网络时，可以通过选择如何构建网络来利用领域专业知识。哪些变量可能会相互影响，或者是独立的，或者是有条件独立的？一般来说，贝叶斯网络的拓扑是由人工构建的，然后在真实世界的数据上进行训练和评估。
贝叶斯网络可以解决三门问题。

三门问题（Monty Hall problem）亦称为蒙提霍尔问题、蒙特霍问题或蒙提霍尔悖论，大致出自美国的电视游戏节目Let’s Make a Deal。问题名字来自该节目的主持人蒙提·霍尔（Monty Hall）。参赛者会看见三扇关闭了的门，其中一扇的后面有一辆汽车，选中后面有车的那扇门可赢得该汽车，另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门，但未去开启它的时候，节目主持人开启剩下两扇门的其中一扇，露出其中一只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。 问题是：换另一扇门会否增加参赛者赢得汽车的机率。如果严格按照上述的条件，那么答案是会。不换门的话，赢得汽车的几率是1/3。换门的话，赢得汽车的几率是2/3。

以下模拟之：

  1. from IPython.display import Image
  2. Image('images/monty.png')

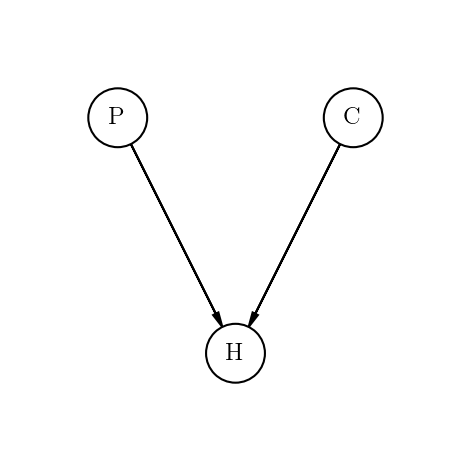
monty.png

  1. from pgmpy.models import BayesianModel
  2. from pgmpy.factors.discrete import TabularCPD
  4. # Defining the network structure
  5. model = BayesianModel([('C', 'H'), ('P', 'H')])
  7. # Defining the CPDs:
  8. cpd_c = TabularCPD('C', 3, [[0.33], [0.33], [0.33]])
  9. cpd_p = TabularCPD('P', 3, [[0.33], [0.33], [0.33]])
  10. cpd_h = TabularCPD('H', 3, [[0, 0, 0, 0, 0.5, 1, 0, 1, 0.5], 
  11.                             [0.5, 0, 1, 0, 0, 0, 1, 0, 0.5], 
  12.                             [0.5, 1, 0, 1, 0.5, 0, 0, 0, 0]],
  13.                   evidence=['C', 'P'], evidence_card=[3, 3])
  15. # Associating the CPDs with the network structure.
  16. model.add_cpds(cpd_c, cpd_p, cpd_h)
  18. # Some other methods
  19. model.get_cpds()
  20. """
  21. [<TabularCPD representing P(C:3) at 0x7f423cc88a58>,
  22.  <TabularCPD representing P(P:3) at 0x7f4310676198>,
  23.  <TabularCPD representing P(H:3 | C:3, P:3) at 0x7f423cc88ac8>]
  24. """
  26. model.check_model()
  28. # Infering the posterior probability 
  29. from pgmpy.inference import VariableElimination
  31. infer = VariableElimination(model)
  32. posterior_p = infer.query(['P'], evidence={'C': 0, 'H': 2})
  33. print(posterior_p)
  34. """
  35. +-----+----------+
  36. | P   |   phi(P) |
  37. |-----+----------|
  38. | P_0 |   0.3333 |
  39. | P_1 |   0.6667 |
  40. | P_2 |   0.0000 |
  41. +-----+----------+
  42. """

0.2.B 先验概率选择

如果试图训练贝叶斯分类器，从实验数据中提取基线先验知识将容易些。然而在其他情况下，忽视的是真实完整的，所以不想将任何不切实际的内容作为先验知识。在诸如确定某人性别等事情的情况下，处理这种情况的基本方式是设定相等的基线：50%的机会是女性，50%的机会是男性。
有一个数学理论证明了这种方法的正确性：使用具有最大熵的先验分布。在概率分布的熵衡量的是概率分布中的不确定性，所以选择使熵最大化的先验知识意味着没有任何先验知识。
那么如果0.2 统计学 - 图85是一个具有0.2 统计学 - 图86个可能状态的离散变量，那么熵定义为：
0.2 统计学 - 图87%0A#card=math&code=H%5BT%5D%20%3D%20-%5Csum%7Bt%3D1%7D%5E%7Bn%7Dp_t%5Cln%28p_t%29%0A&id=QEg6A)
在这种情况下，0.2 统计学 - 图88#card=math&code=-%5Cln%28p_i%29&id=YwXvW)测量得到特定结果0.2 统计学 - 图89，0.2 统计学 - 图90#card=math&code=-p_i%5Cln%28p_i%29&id=lEi1B)是0.2 统计学 - 图91对整体熵的贡献。如果0.2 统计学 - 图92为1，那么0.2 统计学 - 图93#card=math&code=%5Cln%28p_t%29&id=zjkT4)将为0，那么0.2 统计学 - 图94对熵没有贡献。相反，如果0.2 统计学 - 图95非常小，那么事件0.2 统计学 - 图96的信息量则很大，但是由于事件0.2 统计学 - 图97的发生概率很低，所以事件0.2 统计学 - 图98对熵的贡献也很小。直观地说，应该有一个使熵最大化的“最佳点”，事实证明，可以通过将每个点0.2 统计学 - 图99设置为常数0.2 统计学 - 图100来获取此点。
这个概念对连续概率分布具有类似的意义：
0.2 统计学 - 图101%20%5Cln%20(f(t))%20dt%0A#card=math&code=H%5BT%5D%20%3D%20-%5Cint%20f%28t%29%20%5Cln%20%28f%28t%29%29%20dt%0A&id=EunBp)
与离散情况类似，如果存在一个有限的间隔，则最大熵分布是连贯的，并且它是一个常数值：
0.2 统计学 - 图102%20%3D%20%5Cfrac%7B1%7D%7Bx%7Bmax%7D%20-%20x%7Bmin%7D%7D%0A#card=math&code=f%28x%29%20%3D%20%5Cfrac%7B1%7D%7Bx%7Bmax%7D%20-%20x_%7Bmin%7D%7D%0A&id=Fx9kc)