0.1 概率

0.1.1 抛硬币：伯努利随机变量

最简单的概率模型就是抛硬币，假设掷到正面的概率是，则掷反面的概率就是，从概率的角度来说，抛硬币就是“伯努利随机变量”，表示为#card=math&code=Bernoulli%28p%29&id=BiyDE)。
假设正面概率为0.7，反面概率为0.3，这样的分配称为“概率质量函数”。
在很多情况下，有些支出与随机的不同收入相关。例如每次抛出正面给5元，反面赔2元，那平均支出就是

对这个结果的正确解释是，如果抛硬币次，其中是一个非常大的数字，那将赚取元。

在随机事件的大量重复出现中，往往呈现几乎必然的规律，这个规律就是大数定律。 通俗地说，这个定理就是，在试验不变的条件下，重复试验多次，随机事件的频率近似于它的概率。偶然中包含着某种必然。

以下模拟之：

# https://github.com/sijichun/MathStatsCode/blob/master/notebook_python/LLN_CLT.ipynb
import numpy as np
from numpy import random as nprd
True_P=0.5
def sampling(N):
    ## 产生Bernouli样本
    x=nprd.rand(N)<True_P
    return x
M=10000 #模拟次数
xbar=np.zeros(M)
N=np.array([i+1 for i in range(M)])
x=sampling(M)
for i in range(M):
    if i==0:
        xbar[i]=x[i]
    else:
        xbar[i]=(x[i]+xbar[i-1]*i)/(i+1)
## 导入matplotlib
import matplotlib.pyplot as plt 
## 使图形直接插入到jupyter中
%matplotlib inline
# 设定图像大小
plt.rcParams['figure.figsize'] = (10.0, 8.0)
plt.plot(N,xbar,label=r'$\bar{x}$',color='pink') ## xbar
xtrue=np.ones(M)*True_P
plt.plot(N,xtrue,label=r'$0.5$',color='black') ## true xbar
plt.xlabel('N')
plt.ylabel(r'$\bar{x}$')
plt.legend(loc='upper right', frameon=True)
plt.show() ## 画图

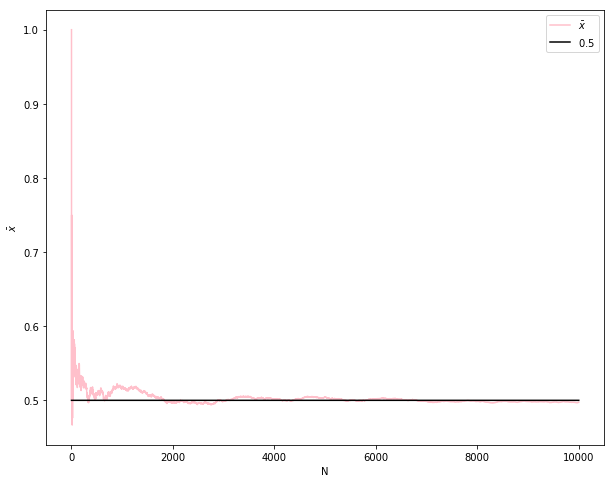
简单来说，大数定律讲的是，样本容量极大时，样本的均值必然趋近于总体的期望。

0.1.2 掷飞镖：均匀随机变量

伯努利随机变量是离散型随机变量的最简单类型。与此相反的随机变量被称为“连续型”随机变量，可在数值范围内取任意值。
最简单的连续型随机变量是均匀随机变量，有时称为，始终在数字和之间，也同样可能为取值范围内的任意位置。
对于离散随机变量，概率质量函数为每个可能的结果分配一个有限的概率。对于连续随机变量，其输出具体值的概率几乎为0，但其输出在特定区间的概率则大得多。

0.1.3 均匀分布和伪随机数

%3C%2Ftitle%3E%0A%3Cdefs%20aria-hidden%3D%22true%22%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-55%22%20d%3D%22M107%20637Q73%20637%2071%20641Q70%20643%2070%20649Q70%20673%2081%20682Q83%20683%2098%20683Q139%20681%20234%20681Q268%20681%20297%20681T342%20682T362%20682Q378%20682%20378%20672Q378%20670%20376%20658Q371%20641%20366%20638H364Q362%20638%20359%20638T352%20638T343%20637T334%20637Q295%20636%20284%20634T266%20623Q265%20621%20238%20518T184%20302T154%20169Q152%20155%20152%20140Q152%2086%20183%2055T269%2024Q336%2024%20403%2069T501%20205L552%20406Q599%20598%20599%20606Q599%20633%20535%20637Q511%20637%20511%20648Q511%20650%20513%20660Q517%20676%20519%20679T529%20683Q532%20683%20561%20682T645%20680Q696%20680%20723%20681T752%20682Q767%20682%20767%20672Q767%20650%20759%20642Q756%20637%20737%20637Q666%20633%20648%20597Q646%20592%20598%20404Q557%20235%20548%20205Q515%20105%20433%2042T263%20-22Q171%20-22%20116%2034T60%20167V183Q60%20201%20115%20421Q164%20622%20164%20628Q164%20635%20107%20637Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-6E%22%20d%3D%22M21%20287Q22%20293%2024%20303T36%20341T56%20388T89%20425T135%20442Q171%20442%20195%20424T225%20390T231%20369Q231%20367%20232%20367L243%20378Q304%20442%20382%20442Q436%20442%20469%20415T503%20336T465%20179T427%2052Q427%2026%20444%2026Q450%2026%20453%2027Q482%2032%20505%2065T540%20145Q542%20153%20560%20153Q580%20153%20580%20145Q580%20144%20576%20130Q568%20101%20554%2073T508%2017T439%20-10Q392%20-10%20371%2017T350%2073Q350%2092%20386%20193T423%20345Q423%20404%20379%20404H374Q288%20404%20229%20303L222%20291L189%20157Q156%2026%20151%2016Q138%20-11%20108%20-11Q95%20-11%2087%20-5T76%207T74%2017Q74%2030%20112%20180T152%20343Q153%20348%20153%20366Q153%20405%20129%20405Q91%20405%2066%20305Q60%20285%2060%20284Q58%20278%2041%20278H27Q21%20284%2021%20287Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-69%22%20d%3D%22M184%20600Q184%20624%20203%20642T247%20661Q265%20661%20277%20649T290%20619Q290%20596%20270%20577T226%20557Q211%20557%20198%20567T184%20600ZM21%20287Q21%20295%2030%20318T54%20369T98%20420T158%20442Q197%20442%20223%20419T250%20357Q250%20340%20236%20301T196%20196T154%2083Q149%2061%20149%2051Q149%2026%20166%2026Q175%2026%20185%2029T208%2043T235%2078T260%20137Q263%20149%20265%20151T282%20153Q302%20153%20302%20143Q302%20135%20293%20112T268%2061T223%2011T161%20-11Q129%20-11%20102%2010T74%2074Q74%2091%2079%20106T122%20220Q160%20321%20166%20341T173%20380Q173%20404%20156%20404H154Q124%20404%2099%20371T61%20287Q60%20286%2059%20284T58%20281T56%20279T53%20278T49%20278T41%20278H27Q21%20284%2021%20287Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-66%22%20d%3D%22M118%20-162Q120%20-162%20124%20-164T135%20-167T147%20-168Q160%20-168%20171%20-155T187%20-126Q197%20-99%20221%2027T267%20267T289%20382V385H242Q195%20385%20192%20387Q188%20390%20188%20397L195%20425Q197%20430%20203%20430T250%20431Q298%20431%20298%20432Q298%20434%20307%20482T319%20540Q356%20705%20465%20705Q502%20703%20526%20683T550%20630Q550%20594%20529%20578T487%20561Q443%20561%20443%20603Q443%20622%20454%20636T478%20657L487%20662Q471%20668%20457%20668Q445%20668%20434%20658T419%20630Q412%20601%20403%20552T387%20469T380%20433Q380%20431%20435%20431Q480%20431%20487%20430T498%20424Q499%20420%20496%20407T491%20391Q489%20386%20482%20386T428%20385H372L349%20263Q301%2015%20282%20-47Q255%20-132%20212%20-173Q175%20-205%20139%20-205Q107%20-205%2081%20-186T55%20-132Q55%20-95%2076%20-78T118%20-61Q162%20-61%20162%20-103Q162%20-122%20151%20-136T127%20-157L118%20-162Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-6F%22%20d%3D%22M201%20-11Q126%20-11%2080%2038T34%20156Q34%20221%2064%20279T146%20380Q222%20441%20301%20441Q333%20441%20341%20440Q354%20437%20367%20433T402%20417T438%20387T464%20338T476%20268Q476%20161%20390%2075T201%20-11ZM121%20120Q121%2070%20147%2048T206%2026Q250%2026%20289%2058T351%20142Q360%20163%20374%20216T388%20308Q388%20352%20370%20375Q346%20405%20306%20405Q243%20405%20195%20347Q158%20303%20140%20230T121%20120Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-72%22%20d%3D%22M21%20287Q22%20290%2023%20295T28%20317T38%20348T53%20381T73%20411T99%20433T132%20442Q161%20442%20183%20430T214%20408T225%20388Q227%20382%20228%20382T236%20389Q284%20441%20347%20441H350Q398%20441%20422%20400Q430%20381%20430%20363Q430%20333%20417%20315T391%20292T366%20288Q346%20288%20334%20299T322%20328Q322%20376%20378%20392Q356%20405%20342%20405Q286%20405%20239%20331Q229%20315%20224%20298T190%20165Q156%2025%20151%2016Q138%20-11%20108%20-11Q95%20-11%2087%20-5T76%207T74%2017Q74%2030%20114%20189T154%20366Q154%20405%20128%20405Q107%20405%2092%20377T68%20316T57%20280Q55%20278%2041%20278H27Q21%20284%2021%20287Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-6D%22%20d%3D%22M21%20287Q22%20293%2024%20303T36%20341T56%20388T88%20425T132%20442T175%20435T205%20417T221%20395T229%20376L231%20369Q231%20367%20232%20367L243%20378Q303%20442%20384%20442Q401%20442%20415%20440T441%20433T460%20423T475%20411T485%20398T493%20385T497%20373T500%20364T502%20357L510%20367Q573%20442%20659%20442Q713%20442%20746%20415T780%20336Q780%20285%20742%20178T704%2050Q705%2036%20709%2031T724%2026Q752%2026%20776%2056T815%20138Q818%20149%20821%20151T837%20153Q857%20153%20857%20145Q857%20144%20853%20130Q845%20101%20831%2073T785%2017T716%20-10Q669%20-10%20648%2017T627%2073Q627%2092%20663%20193T700%20345Q700%20404%20656%20404H651Q565%20404%20506%20303L499%20291L466%20157Q433%2026%20428%2016Q415%20-11%20385%20-11Q372%20-11%20364%20-4T353%208T350%2018Q350%2029%20384%20161L420%20307Q423%20322%20423%20345Q423%20404%20379%20404H374Q288%20404%20229%20303L222%20291L189%20157Q156%2026%20151%2016Q138%20-11%20108%20-11Q95%20-11%2087%20-5T76%207T74%2017Q74%2030%20112%20181Q151%20335%20151%20342Q154%20357%20154%20369Q154%20405%20129%20405Q107%20405%2092%20377T69%20316T57%20280Q55%20278%2041%20278H27Q21%20284%2021%20287Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-28%22%20d%3D%22M94%20250Q94%20319%20104%20381T127%20488T164%20576T202%20643T244%20695T277%20729T302%20750H315H319Q333%20750%20333%20741Q333%20738%20316%20720T275%20667T226%20581T184%20443T167%20250T184%2058T225%20-81T274%20-167T316%20-220T333%20-241Q333%20-250%20318%20-250H315H302L274%20-226Q180%20-141%20137%20-14T94%20250Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-30%22%20d%3D%22M96%20585Q152%20666%20249%20666Q297%20666%20345%20640T423%20548Q460%20465%20460%20320Q460%20165%20417%2083Q397%2041%20362%2016T301%20-15T250%20-22Q224%20-22%20198%20-16T137%2016T82%2083Q39%20165%2039%20320Q39%20494%2096%20585ZM321%20597Q291%20629%20250%20629Q208%20629%20178%20597Q153%20571%20145%20525T137%20333Q137%20175%20145%20125T181%2046Q209%2016%20250%2016Q290%2016%20318%2046Q347%2076%20354%20130T362%20333Q362%20478%20354%20524T321%20597Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-2C%22%20d%3D%22M78%2035T78%2060T94%20103T137%20121Q165%20121%20187%2096T210%208Q210%20-27%20201%20-60T180%20-117T154%20-158T130%20-185T117%20-194Q113%20-194%20104%20-185T95%20-172Q95%20-168%20106%20-156T131%20-126T157%20-76T173%20-3V9L172%208Q170%207%20167%206T161%203T152%201T140%200Q113%200%2096%2017Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-31%22%20d%3D%22M213%20578L200%20573Q186%20568%20160%20563T102%20556H83V602H102Q149%20604%20189%20617T245%20641T273%20663Q275%20666%20285%20666Q294%20666%20302%20660V361L303%2061Q310%2054%20315%2052T339%2048T401%2046H427V0H416Q395%203%20257%203Q121%203%20100%200H88V46H114Q136%2046%20152%2046T177%2047T193%2050T201%2052T207%2057T213%2061V578Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-29%22%20d%3D%22M60%20749L64%20750Q69%20750%2074%20750H86L114%20726Q208%20641%20251%20514T294%20250Q294%20182%20284%20119T261%2012T224%20-76T186%20-143T145%20-194T113%20-227T90%20-246Q87%20-249%2086%20-250H74Q66%20-250%2063%20-250T58%20-247T55%20-238Q56%20-237%2066%20-225Q221%20-64%20221%20250T66%20725Q56%20737%2055%20738Q55%20746%2060%20749Z%22%3E%3C%2Fpath%3E%0A%3C%2Fdefs%3E%0A%3Cg%20stroke%3D%22currentColor%22%20fill%3D%22currentColor%22%20stroke-width%3D%220%22%20transform%3D%22matrix(1%200%200%20-1%200%200)%22%20aria-hidden%3D%22true%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-55%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-6E%22%20x%3D%22767%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%221368%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-66%22%20x%3D%221713%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-6F%22%20x%3D%222264%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-72%22%20x%3D%222749%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-6D%22%20x%3D%223201%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%224079%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-30%22%20x%3D%224469%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%20x%3D%224969%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%225414%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%225915%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E#card=math&code=Uniform%280%2C1%29&id=tePS9)分布是最基本的概率分布。它是最简单的一个，但也是在数学理论和计算实践中构建更复杂概率分布的基础。例如：

• 如果要模拟#card=math&code=Bernoulli%28p%29&id=OsWPq)随机变量，可以通过模拟#card=math&code=Uniform%280%2C1%29&id=ly7FP)分布中的随机值来实现。如果，则设置=正面，否则设置=反面。
• 如果要模拟加权掷骰子，将[0.0, 1.0]取值范围分成6个区域，其中第个区域的大小与骰子投出第面的概率相同。然后再次从#card=math&code=Uniform%280%2C1%29&id=YHokK)分布中绘制值。掷出的骰子即会落入的 [0.0, 1.0]区间。
• 如果要模拟指数随机变量，从#card=math&code=Uniform%280%2C1%29&id=VBh86)中绘制，然后取#card=math&code=%5Clog%28u%29&id=QPAD2)的倒数。

但是，技术上讲，用计算机程序模拟随机数是不可行的。它们是确定性的机器，只能遵循预定的规则——没有用于翻转硬币的子程序。一般会用“伪随机数”即某种固定生成算法来实现，比如早期的线性同余法。
当然伪随机数也有优点，可以在一开始就手动设置好部分参数，也被称为“种子/seed”。这样做可以使程序变得更加完全确定，并且可以在下次运行中精确地重现相同的结果。

如：

>>> import random
>>> random.random()
0.7006269308810754
>>> random.random()
0.4896124288257575
>>> random.seed(10086)
>>> random.random()
0.043562757723543566
>>> random.random()
0.7994528936212764
>>> random.seed(10086)
>>> random.random()
0.043562757723543566

同一种子10086时，输出随机数相同。

0.1.4 非离散型、非连续型随机变量

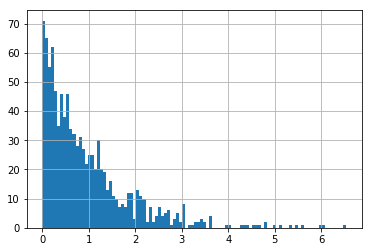
从数学角度而言，随机变量既不离散也不连续。例如以种植树木的高度为例，在给定的时间点中，其中不发芽的一部分高度为0，这是在该高度下的有限概率质量。而那些发芽树木的高度则为在一定范围内的任意值。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
z = np.zeros(1000)
x = np.random.exponential(size=1000)
D = pd.Series(data)
X = pd.Series(x)
(D>0).value_counts().rename({True: ">0", False: "<0"}).plot(kind="pie")
X.hist(bins=100)

0.1.5 期望和标准偏差

通常使用大写字母表示随机变量，小写字母表示变量的特定值。
如果写作是指随机变量的平均值。这里的是指期望值，是均值的另一种形式。

• 不连续随机变量的预期值定义为：

• 连续随机变量的预期值定义为：

%20dx%0A#card=math&code=E%5BX%5D%20%3D%20%5Cint%20xf_x%28x%29%20dx%0A&id=Hkl6C)
通常由表示随机变量的期望值，根据期望值定义某个事物的关键例子是方差和标准偏差。
的方差定义为：

标准差是方差的二次方根：

标准差可以用来粗略衡量X与的距离。

0.1.6 独立概率、边际概率和条件概率

通常需要同时考虑两个随机变量和。如果已知一个变量，能以此了解另一个变量吗？
具体来说，假设变量是离散随机变量，令表示和的概率。
的边际概率为

如果重视一个随机变量而忽略另一个，那么就是概率分布。
另一方面，由已知的值推断的情况，那么就可以在给定的时，得到每个的条件概率：

条件概率在贝叶斯统计中起着重要的作用。
给定，通常想知道的期望值，表达如下：

这些关于的统计值与的取值条件相关，和的相关性定义为：
(Y-%5Cmuy)%5D%7D%7B%5Csigma_x%5Csigma_y%7D%0A#card=math&code=Corr%5BX%2CY%5D%20%3D%20%5Cfrac%7BE%5B%28X-%5Cmu_x%29%28Y-%5Cmu_y%29%5D%7D%7B%5Csigma_x%5Csigma_y%7D%0A&id=XNgnj)
这是随机变量之间的线性关系的度量，其形式为。
如果已知随机变量和中的任一个，并不能获取另一个随机变量的相关信息，则和是独立随机变量。在数学上意味着：

值得注意的是，独立性是一个非常强大的标准，这比仅仅说相关性为0要强得多。

0.1.7 重尾分布

关于概率分布最重要的理解之一就是“重尾”。直观地说，这是指最大值出现的概率。身高就是非重尾的一个很好的例子，因为没有人身高能超过10米。然而净资产是重尾分布，因为偶尔会出现比尔·盖茨。
了解重尾分布很重要，这是因为当事情为重尾分布时，通常用概率分布做的事情都不起作用。
举例，重尾分布的平均值很难估计，如果房间里有100个人，那么这些人的平均净资产可能会有很大的差异，像一个千万富翁就可能极大提高平均净资产。
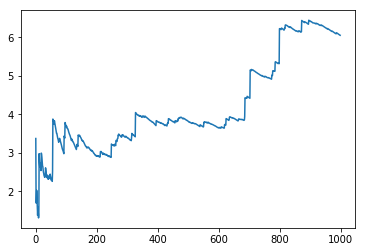
以下通过帕累托分布中抽取重尾序列，模拟次，可见平均值趋涨：

import numpy as np
import matplotlib.pyplot as plt
np.random.seed(10)
N = 1000
sums, means = 0, []
for i in range(1, N):
    sums += np.random.pareto(1)
    means.append(sums/i)
plt.plot(means)

0.1.8 二项分布

二项式(，) 的分布是抛硬币次得到正面的次数，其中每次抛掷正面的独立概率为。
即次抛掷硬币得到次正面的特定序列概率为%5En-k#card=math&code=p%5Ek%281-p%29%5En-k&id=J7TUH)。
如何在次投掷硬币中抛出次正面是一个组合问题，确切公式表示为，即从个元素中选择个元素
!%7D%0A#card=math&code=%5Clgroup%5En_k%5Crgroup%20%3D%20%5Cfrac%7Bn%21%7D%7Bk%21%28n-k%29%21%7D%0A&id=ChW4v)
以下模拟之：

import numpy as np
import pandas as pd
sample = np.random.binomial(200, 0.3)
print(sample)
N = 100
sample = []
for _ in range(N):
    sample.append(np.random.binomial(1, 0.3))
pd.value_counts(sample)
"""
55
0    73
1    27
dtype: int64
"""

0.1.9 泊松分布

泊松分布用于模拟可能发生许多事件的系统，并且所有事件都相互独立，但平均而言，只有少数时间会发生。一个很好的例子就是会有多少人在某一天访问一个网站，世界上有数十亿人可以访问这个网址，但平均而言，也许只有几百人会访问这个网站。
日常生活中，大量事件是有固定频率的，如：

• 某医院平均每小时出生3个婴儿
• 某公司平均每10分钟接到1个电话
• 某超市平均每天销售4包xx牌奶粉
• 某网站平均每分钟有2次访问

它们的特点就是，我们可以预估这些事件的总数，但是没法知道具体的发生时间。已知平均每小时出生3个婴儿，请问下一个小时，会出生几个？有可能一下子出生6个，也有可能一个都不出生。这是我们没法知道的。
泊松分布就是描述某段时间内，事件具体的发生概率。

假设采用二项式(，)分布。将设置得非常大，将设置得足够小，则

式中，是固定常数。
在使得大而小同时不变的约束下，二项分布将收敛于泊松分布。概率质量函数由下式给出：

加入时间维度，
%3Dn)%3De%5E%7B-%5Clambda%20t%7D%5Cfrac%7B(%5Clambda%20t)%5Ek%7D%7Bk!%7D%0A#card=math&code=P%28N%28t%29%3Dn%29%3De%5E%7B-%5Clambda%20t%7D%5Cfrac%7B%28%5Clambda%20t%29%5Ek%7D%7Bk%21%7D%0A&id=xZX8V)
已知1小时内出生3个婴儿的概率，就表示为%3D3)#card=math&code=P%28N%281%29%3D3%29&id=zokah)，那么接下来两个小时，一个婴儿都不出生的概率是0.25%，基本不可能发生。因为：
%3D0)%3D%5Cfrac%7B(3%5Ctimes2)%5E0e%5E%7B-3%5Ctimes2%7D%7D%7B0!%7D%20%5Capprox%200.0025%0A#card=math&code=P%28N%282%29%3D0%29%3D%5Cfrac%7B%283%5Ctimes2%29%5E0e%5E%7B-3%5Ctimes2%7D%7D%7B0%21%7D%20%5Capprox%200.0025%0A&id=MfcCT)
接下来一个小时，至少出生两个婴儿的概率是80%：
%5Cge2)%20%26%3D%201-P(N(1)%3D1)-P(N(1)%3D0)%20%5C%5C%0A%26%3D%201%20-%20%5Cfrac%7B(3%5Ctimes1)%5E1e%5E%7B-3%5Ctimes1%7D%7D%7B1!%7D%20-%20%5Cfrac%7B(3%5Ctimes1)%5E0e%5E%7B-3%5Ctimes1%7D%7D%7B0!%7D%5C%5C%0A%26%3D%201%20-%203e%5E%7B-3%7D%20-%20e%5E%7B-3%7D%20%5C%5C%0A%26%3D%201%20-%204e%5E%7B-3%7D%20%5C%5C%0A%26%5Capprox%200.8009%0A%5Cend%7Balign%7D%0A#card=math&code=%5Cbegin%7Balign%7D%0AP%28N%281%29%5Cge2%29%20%26%3D%201-P%28N%281%29%3D1%29-P%28N%281%29%3D0%29%20%5C%5C%0A%26%3D%201%20-%20%5Cfrac%7B%283%5Ctimes1%29%5E1e%5E%7B-3%5Ctimes1%7D%7D%7B1%21%7D%20-%20%5Cfrac%7B%283%5Ctimes1%29%5E0e%5E%7B-3%5Ctimes1%7D%7D%7B0%21%7D%5C%5C%0A%26%3D%201%20-%203e%5E%7B-3%7D%20-%20e%5E%7B-3%7D%20%5C%5C%0A%26%3D%201%20-%204e%5E%7B-3%7D%20%5C%5C%0A%26%5Capprox%200.8009%0A%5Cend%7Balign%7D%0A&id=M5sjf)
以下模拟之：

import numpy as np
import pandas as pd
sample = np.random.poisson(lam=5, size=5)
print(sample)
N = 100
sample = []
for _ in range(N):
    sample.append(np.random.poisson(5))
pd.value_counts(sample)
"""
[9 4 5 5 4]
4     22
3     15
6     14
5     14
7      9
2      9
10     6
8      6
9      2
1      2
0      1
dtype: int64
"""

0.1.A 正态分布

正态分布是非常重要的一种概率分布，也称为高斯分布。它是典型的钟形曲线，其概率密度函数：
%20%3D%20%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%5Csigma%5E2%7D%7De%5E%7B-(x-%5Cmu)%2F2%5Csigma%5E2%7D%0A#card=math&code=f%28x%29%20%3D%20%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%5Csigma%5E2%7D%7De%5E%7B-%28x-%5Cmu%29%2F2%5Csigma%5E2%7D%0A&id=vnb7j)
式中，是其平均值，是标准偏差。
这种正态分布通常称为#card=math&code=N%28%5Cmu%2C%5Csigma%5E2%29&id=oTGTU)。
正态分布最重要的性质是其概率密度紧密聚集在均值附近，尾巴较小，并且不大可能会出现大量异常值。出于这个原因，简单的用正态分布来拟合数据可能会产生严重问题。通常在进行曲线拟合之前，识别并移除主要异常值是常用方法。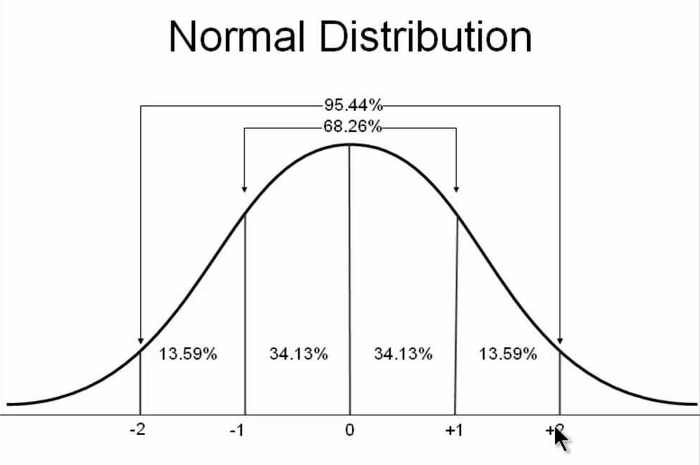

从理论上，正态分布被作为最有名的概率分布，是因为如果有足够多的时间采样并对结果进行平均，许多分布将收敛于正态分布。这适用于二项分布、泊松分布以及任何可能遇到的其他分布。从技术上讲，任何一个分布的平均值和标准偏差都是有限的。
这被归结于“中心极限定理”中：

中心极限定理，设是具有有限的均值和标准差的随机变量。令，，…，是的独立样本序列。然后当趋向于无穷大时： %0A#card=math&code=%5Csqrt%7Bn%7D%5Clgroup%5Cfrac%7B1%7D%7Bn%7D%5Csum%20X_i%20-%20%5Cmu%20%5Crgroup%5Cto%20N%280%2C%5Csigma%5E2%29%0A&id=OIODr)

它是概率论中最重要的一类定理，有广泛的实际应用背景。在自然界与生产中，一些现象受到许多相互独立的随机因素的影响，如果每个因素所产生的影响都很微小时，总的影响可以看作是服从正态分布的。中心极限定理就是从数学上证明了这一现象。最早的中心极限定理是讨论重点，伯努利试验中，事件A出现的次数渐近于正态分布的问题。
以下模拟之：

# https://github.com/sijichun/MathStatsCode/blob/master/notebook_python/LLN_CLT.ipynb
from numpy import random as nprd
def sampling(N):
    ## 产生一组样本，以0.5的概率为z+3，0.5的概率为z-3，其中z~N(0,1)
    d = nprd.rand(N)<0.5
    z = nprd.randn(N)
    x = np.array([z[i]+3 if d[i] else z[i]-3 for i in range(N)])
    return x
N = [2,3,4,10,100,1000] # sample size
M = 2000
MEANS = []
for n in N:
    mean_x = np.zeros(M)
    for i in range(M):
        x = sampling(n)
        mean_x[i] = np.mean(x)/np.sqrt(10/n) ## 标准化，因为var(x)=10
    MEANS.append(mean_x)
## 导入matplotlib
import matplotlib.pyplot as plt
import matplotlib.mlab as mlab
## 使图形直接插入到jupyter中
%matplotlib inline
# 设定图像大小
plt.rcParams['figure.figsize'] = (10.0, 8.0)
x = sampling(1000)
plt.xlabel('x')
plt.ylabel('Density')
plt.title('Histogram of Mixed Normal')
plt.hist(x, bins=30, normed=1) ## histgram
plt.show() ## 画图
## 均值
ax1 = plt.subplot(2,3,1)
ax2 = plt.subplot(2,3,2)
ax3 = plt.subplot(2,3,3)
ax4 = plt.subplot(2,3,4)
ax5 = plt.subplot(2,3,5)
ax6 = plt.subplot(2,3,6)
## normal density
x = np.linspace(-3,3,100)
d = [1.0/np.sqrt(2*np.pi)*np.exp(-i**2/2) for i in x]
def plot_density(ax,data,N):
    ax.hist(data, bins=30, normed=1) ## histgram
    ax.plot(x, d)
    ax.set_title(r'Histogram of $\bar{x}$:N=%d' % N)
plot_density(ax1,MEANS[0],N[0])
plot_density(ax2,MEANS[1],N[1])
plot_density(ax3,MEANS[2],N[2])
plot_density(ax4,MEANS[3],N[3])
plot_density(ax5,MEANS[4],N[4])
plot_density(ax6,MEANS[5],N[5])
plt.show() ## 画图

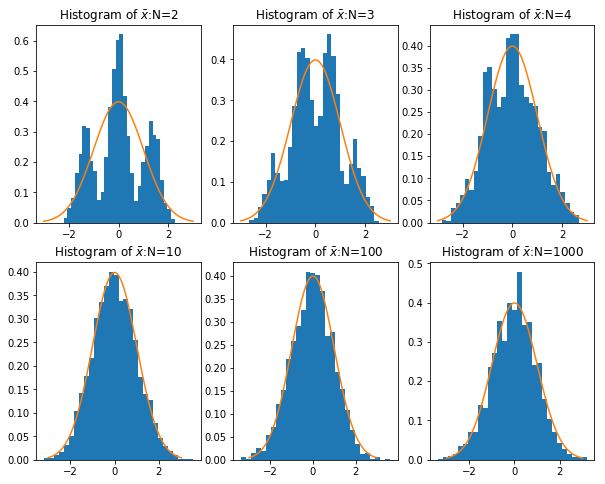
简单来说，**中心极限定理讲的是，样本容量极大时，样本均值的抽样分布趋近于正态分布。这和样本所属的总体的分布的类型无关，样本所属总体的分布可以是正态分布，也可以不是。

**

0.1.B 多元正态分布

如果我们以显著的方式推广上述分布变量到更高维度，如正态分布，正态分布可以定义任意维度。密度函数类似于一个山丘，它在分布的平均值处达到峰值，并且总体呈现为椭圆形。

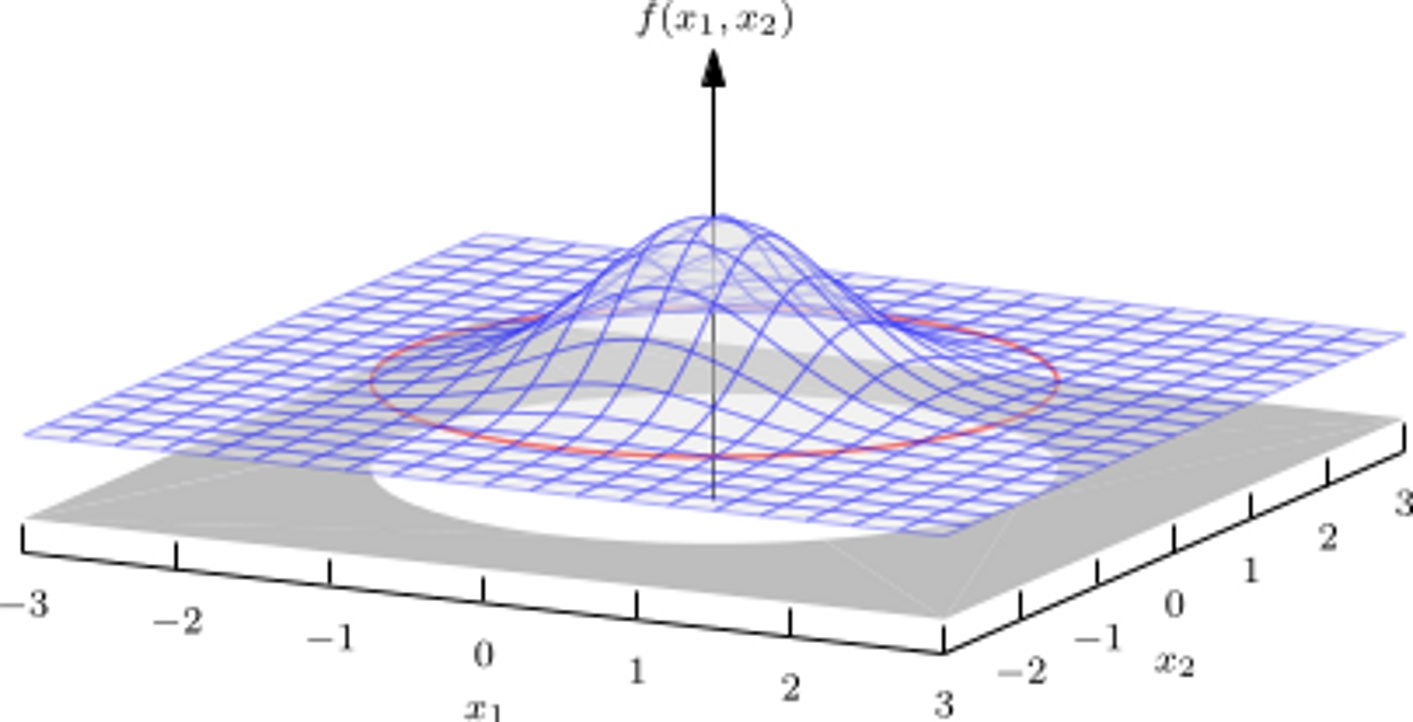
应该注意到，椭圆体可以向任意方向伸展，不必沿着某一个轴伸展。

0.1.C 指数分布

指数分布在其模拟某些事件发生的时间或事件之间的时间长度时最有用。比方说，对于进入商店的人，每个时刻人们走进商店的概率是一个较小的固定值，并且每个时刻都是相互独立的。在这种情况下，事件之间的时间量将呈指数分布。
指数分布是事件的时间间隔的概率。

• 婴儿出生的时间间隔
• 来电的时间间隔
• 奶粉销售的时间间隔
• 网站访问的时间间隔

指数分布由其平均值（事件之间的平均时间）进行参数化。有时会使用（事件发生的平均速率）对其进行参数化，其概率密度函数：
%3D%5Cleft%5C%7B%0A%5Cbegin%7Barray%7D%7Brcl%7D%0A%5Cfrac%7B1%7D%7B%5Ctheta%7De%5E%7B-x%2F%5Ctheta%7D%20%26%20%26%20%7Bx%5Cge0%7D%5C%5C%0A0%20%26%20%26%20%7Bother%7D%5C%5C%0A%5Cend%7Barray%7D%20%5Cright.%0A#card=math&code=f%28x%29%3D%5Cleft%5C%7B%0A%5Cbegin%7Barray%7D%7Brcl%7D%0A%5Cfrac%7B1%7D%7B%5Ctheta%7De%5E%7B-x%2F%5Ctheta%7D%20%26%20%26%20%7Bx%5Cge0%7D%5C%5C%0A0%20%26%20%26%20%7Bother%7D%5C%5C%0A%5Cend%7Barray%7D%20%5Cright.%0A&id=xgulJ)
指数分布的公式可以从泊松分布推断出来，引用上例，
如果下一个婴儿要间隔时间 t ，就等同于 t 之内没有任何婴儿出生。
%20%26%3D%20P(N(t)%3D0)%20%3D%20%5Cfrac%7B(%5Clambda%20t)%5E0e%5E%7B-%5Clambda%20t%7D%7D%7B0!%7D%5C%5C%0A%26%3D%20e%5E%7B-%5Clambda%20t%7D%0A%5Cend%7Balign%7D%0A#card=math&code=%5Cbegin%7Balign%7D%0AP%28X%20%3E%20t%29%20%26%3D%20P%28N%28t%29%3D0%29%20%3D%20%5Cfrac%7B%28%5Clambda%20t%29%5E0e%5E%7B-%5Clambda%20t%7D%7D%7B0%21%7D%5C%5C%0A%26%3D%20e%5E%7B-%5Clambda%20t%7D%0A%5Cend%7Balign%7D%0A&id=uTiMe)
反过来，事件在时间 t 之内发生的概率，就是1减去上面的值。
%20%3D%201%20-%20P(X%20%5Cgt%20t)%20%3D%201%20-%20e%5E%7B-%5Clambda%20t%7D%0A#card=math&code=P%28X%20%5Cle%20t%29%20%3D%201%20-%20P%28X%20%5Cgt%20t%29%20%3D%201%20-%20e%5E%7B-%5Clambda%20t%7D%0A&id=RXGvb)
接下来15分钟，会有婴儿出生的概率是52.76%
%20%26%3D%201%20-%20e%5E%7B-3%5Ctimes0.25%7D%5C%5C%0A%26%5Capprox%200.5276%0A%5Cend%7Balign%7D%0A#card=math&code=%5Cbegin%7Balign%7D%0AP%28X%20%5Cle%200.25%20%29%20%26%3D%201%20-%20e%5E%7B-3%5Ctimes0.25%7D%5C%5C%0A%26%5Capprox%200.5276%0A%5Cend%7Balign%7D%0A&id=lmKQ5)
接下来的15分钟到30分钟，会有婴儿出生的概率是24.92%
%20%26%3D%20P(X%20%5Cle%200.5)%20-%20P(X%20%5Cle%200.25)%5C%5C%0A%26%3D%20(1-e%5E%7B-3%5Ctimes0.5%7D)-(1-e%5E%7B-3%5Ctimes0.25%7D)%20%5C%5C%0A%26%3D%20e%5E%7B-0.75%7D%20-%20e%5E%7B-1.5%7D%20%5C%5C%0A%26%5Capprox%200.2492%0A%5Cend%7Balign%7D%0A#card=math&code=%5Cbegin%7Balign%7D%0AP%280.25%20%5Cle%20X%20%5Cle%200.5%29%20%26%3D%20P%28X%20%5Cle%200.5%29%20-%20P%28X%20%5Cle%200.25%29%5C%5C%0A%26%3D%20%281-e%5E%7B-3%5Ctimes0.5%7D%29-%281-e%5E%7B-3%5Ctimes0.25%7D%29%20%5C%5C%0A%26%3D%20e%5E%7B-0.75%7D%20-%20e%5E%7B-1.5%7D%20%5C%5C%0A%26%5Capprox%200.2492%0A%5Cend%7Balign%7D%0A&id=zUinB)
以下模拟之：

import numpy as np
import pandas as pd
sample = np.random.exponential(10)
print(sample)
N = 10
sample = []
for _ in range(N):
    sample.append(np.random.exponential(1))
pd.value_counts(sample)
"""
34.293011008718764
1.426454    1
0.205591    1
0.119978    1
0.404349    1
0.220207    1
0.463974    1
0.495403    1
0.301081    1
2.966221    1
0.009234    1
dtype: int64
"""

在很多应用中，指数分布的关键属性是“无记忆”。无论等待事件发生的时间有多久，剩余的等待时间仍然遵循相同的指数分布。一个事件在下一个时刻是否发生，与之前已发生的其他时间无关。
指数分布的无记忆特性通常被认为是重尾分布与非重尾分布的分界线。如果已经等待了一个事件发生的时间为，那么期望等待的时间比刚开始的时间长还是短呢？指数随机变量不会有任何结果。相比之下，20岁的人可能倾向于再等20多年，但90岁的人可能不会。因此年龄并不是重尾的。街上随机的一个人不太可能是百万富翁，但是如果碰巧挑选到的人都至少有80万元，那么百万富翁的可能性就大很多。因此，净资产是重尾的。

0.1.D 对数正态分布

重尾分布是对数正态分布，对其理解和模拟很简单。同时，对数正态分布的平均值和标准差都是有限的。对于所有现实世界的现象都是如此。
该分布中有一个明显的峰值，且峰值大于0，峰值的左侧迅速下降，在时变为0.0，在右边逐渐变窄，会使其有规律地出现大的异常值。对数正态分布最好这样考虑，从正态(，)中抽取一个值，则是对数正态分布的。
以下模拟之：

import numpy as np
import pandas as pd
sample = np.random.lognormal(1, 2)
print(sample)
N = 10
sample = []
for _ in range(N):
    sample.append(np.random.lognormal(1, 2))
pd.value_counts(sample)
"""
18.761595456554964
0.232312     1
9.743775     1
18.472365    1
21.047856    1
61.887021    1
13.400393    1
37.689687    1
5.035124     1
0.026245     1
0.156932     1
dtype: int64
"""

这就是说，财富的对数值满足正态分布。如果平均财富是10,000元，那么1000元～10,000元之间的穷人（比平均值低一个数量级，宽度为9000）与10,000元~100,000元之间的富人（比平均值高一个数量级，宽度为90,000）人数一样多。因此，财富曲线左侧的范围比较窄，右侧出现重尾。

0.1.E 熵

熵是一种衡量随机变量“随机性”的方法，概念来自信息论领域。直观地说，公平硬币的随机性要高于99%出现正面的硬币。同样，如果一个正态分布的标准差很小，那么它的概率质量将紧紧地围绕它的平均值分布，且它比更大标准差的分布随机性更差。
如果随机变量是离散的，熵即
%0A#card=math&code=H%5BX%5D%20%3D%20E%5BSurpise%5BX%5D%5D%20%3D%20-%5Csum_xp_x%5Cln%28p_x%29%0A&id=y7tYQ)
如果随机变量是连续的，熵即
%20%5Cln(f(x))%20dx%0A#card=math&code=H%5BX%5D%20%3D%20-%5Cint%20f%28x%29%20%5Cln%28f%28x%29%29%20dx%0A&id=citQg)
我们很少直接计算熵，但概念无处不在。