05. 矩阵乘法

C = A * B (A[m,k], B[k, n ], C[m, n])。一个线程负责计算C中的一个元素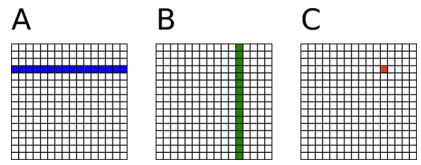

矩阵A：；矩阵B：；：

// Matrix multiplication on the (CPU) host
void main(){
    define A, B, C
        for i = 0 to M-1 do  # 行索引
            for j = 0 to N-1 do  # 列索引
                /* compute element C(i,j) */
                for k = 0 to K-1 do
                    C(i,j) <= C(i,j) + A(i,k) * B(k,j)
                end
            end
        end
}

矩阵乘法的时间复杂度为：
矩阵相加的时间复杂度为：

void main(){
    define A_cpu, B_cpu, C_cpu in the CPU memory;
    define A_gpu, B_gpu, C_gpu in the GPU memory;

    memcopy A_cpu to A_gpu;
    memcopy B_cpu to B_gpu;

    dim3 dimBlock(16, 16);
    dim3 dimGrid(N/dimBlock.x, M/dimBlock.y);

    matrixMul<<<dimGrid, dimBlock>>>(A_gpu,B_gpu,C_gpu,K);  // 核函数

    memcopy C_gpu to C_cpu;
    }

1. 频繁访问缓存的程序不适用GPU编程
2. 流程复杂的程序不适用GPU编程
3. 计算密集的程序适合GPU 编程
4. 一个线程束只有一个控制单元，并行度高的程序适合GPU编程

矩阵乘法无复杂的访问读写；无复杂流程；计算简单；结果中每个相加的元素都互不影响。

__global__ void matrixMul(A_gpu,B_gpu,C_gpu,K){
    temp <= 0;
    i <= blockIdx.y * blockDim.y + threadIdx.y;   // Row i of matrix C
    j <= blockIdx.x * blockDim.x + threadIdx.x ;  // Column j of matrix C
    for k = 0 to K-1 do
        accu <= accu + A_gpu(i,k) * B_gpu(k,j);
    end

    C_gpu(i,j) <= accu
}

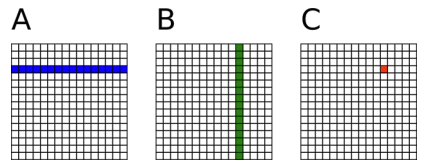
C = A * B (A[m,k], B[k, n ], C[m, n])

• 一个线程负责计算C中的一个元素
• A中的每一行从全局内存中载入N次
• B中的每一列从全局内存中载入M次

比如说：计算C[1, 12]、C[2, 12]、C[3, 12]时，每次都要使用B的第12列，所以B中的每一列都要加载C的行数，也就是A的行数M次。

矩阵乘法运算，每个线程都要读取A的一整行和B的一整列。A矩阵中的每个点需要被读N次，B矩阵中的每个点需要被读M次。

所以做一次矩阵乘法，需要访问全局内存次。可以将多次访问的数据放到共享内存中，减少重复读取的次数，并充分利用共享内存的延迟低的优势。

共享内存出现在线程块中，线程块由若干彼此独立的线程和一块共享内存组成，共享内存可以由线程块内的所有线程访问的，线程块内可以通过同步函数来同步线程块内所有线程，进行统一的时钟同步操作。

CUDA内存读写速度

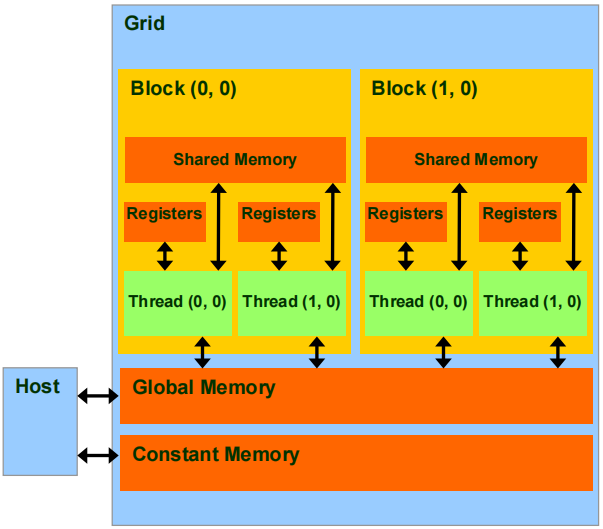	每个线程硬件上读写速度对比 - 对于每个线程而言，有各自独立的线程寄存器，这种线程寄存器的读写周期(~1 周期) - 线程块共享内存(~5 周期) - Grid全局内存(~500 周期) - Grid常量内存(~5 周期)

线程块中的共享内存和Grid全局内存在硬件上的读写速度有100倍的差距，所以我们可以把频繁访问的数据放到共享内存中，来提升速度。 :::info 使用好共享内存，可以很好的解决GPU的读写瓶颈。 :::

CUDA中的共享内存
一种特殊类型的内存，其内容在源代码中被显式声明和使用

• 位于处理器中
• 以更高的速度访问(延迟&吞吐)
• 仍然被内存访问指令访问
• 在计算机体系结构中通常称为暂存存储器

共享内存特点

• 读取速度等同于缓存，在很多显卡上，缓存和共享内存使用的是同一块硬件，并且可以配置大小
• 共享内存属于线程块，可以被一个线程块内的所有线程访问
• 共享内存的两种申请空间方式：静态申请和动态申请，API不同。
• 共享内存的大小只有几十K，过度使用共享内存会降低程序的并行性

申请共享内存

1. 申请

• __shared__关键字

1. 申请方式

• 静态申请
• 动态申请

1. 使用

• 将每个线程从全局索引位置读取元素，将它存储到共享内存之中。
• 注意数据存在着交叉，应该将边界上的数据拷贝进来。
• 块内线程同步：__syncthreads()。

__syncthreads()线程同步函数使用方法

• __syncthreads()是cuda的内建函数，用于块内线程通信，防止时序错乱问题。
• 对可以到达__syncthreads()的线程进行同步，而不是等待块内所有其他线程再同步。

右边代码，不是所有的线程进入到第一个if，还有一部分线程进入到else，如果if中的线程对共享内存中的数据进行修改，此时无法和else中的线程进行同步，那么else中的线程读取到的还是原始共享内存中的数据，就会发生错误。

所以，在使用共享内存和同步函数时，尽量不要存在复杂的分支判断，进而保证需要同步的线程都能够被同步到。

静态申请共享内存：

• 共享内存大小明确

  __global__ void staticReverse(int *d, int n) { 
    __shared__ int s[64]; 
    int t = threadIdx.x; 
    int tr = n-t-1; 
    s[t] = d[t]; 
    __syncthreads(); 
    d[t] = s[tr]; 
  }
  staticReverse<<<1,n>>>(d_d, n);
  

• 共享内存大小不明确

  __global__ void dynamicReverse(int *d, int n) { 
    extern __shared__ int s[]; // 不用明确内存容量；extern 关键字修饰，告诉编译器是动态申请
    int t = threadIdx.x; 
    int tr = n-t-1; 
    s[t] = d[t]; 
    __syncthreads(); 
    d[t] = s[tr]; 
  }
  dynamicReverse<<<1,n,n*sizeof(int)>>>(d_d, n); // 需要明确告诉核函数，需要分配的共享内存的大小
  

思路：使用共享内存复用全局内存数据

• 每个输入元素被WIDTH个线程读取：将频繁读取的数据放到共享内存中；
• 将每个元素加载到共享内存中并让多个线程使用本地版本以减少内存带宽：一次计算得到多个C中的元素

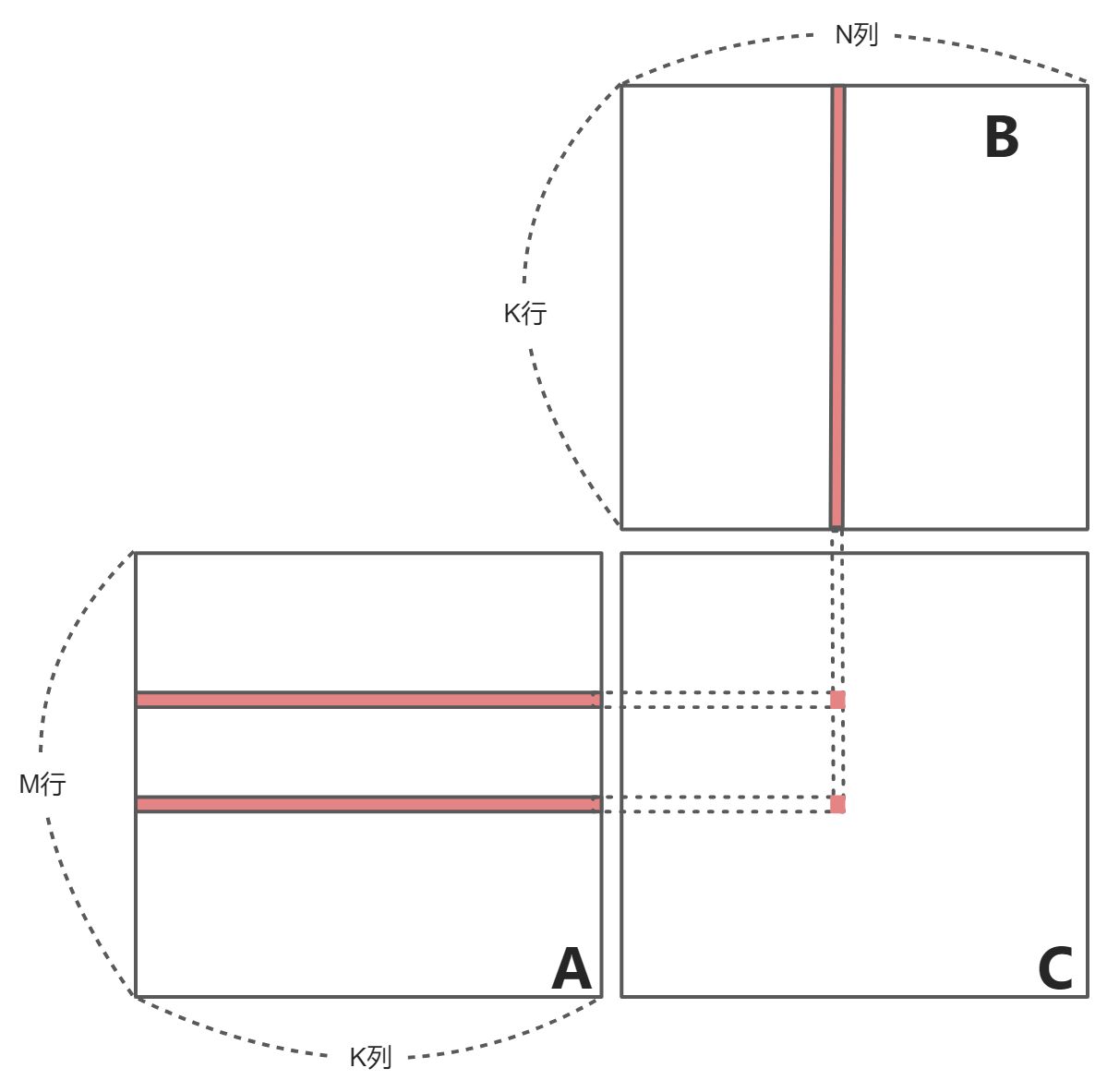
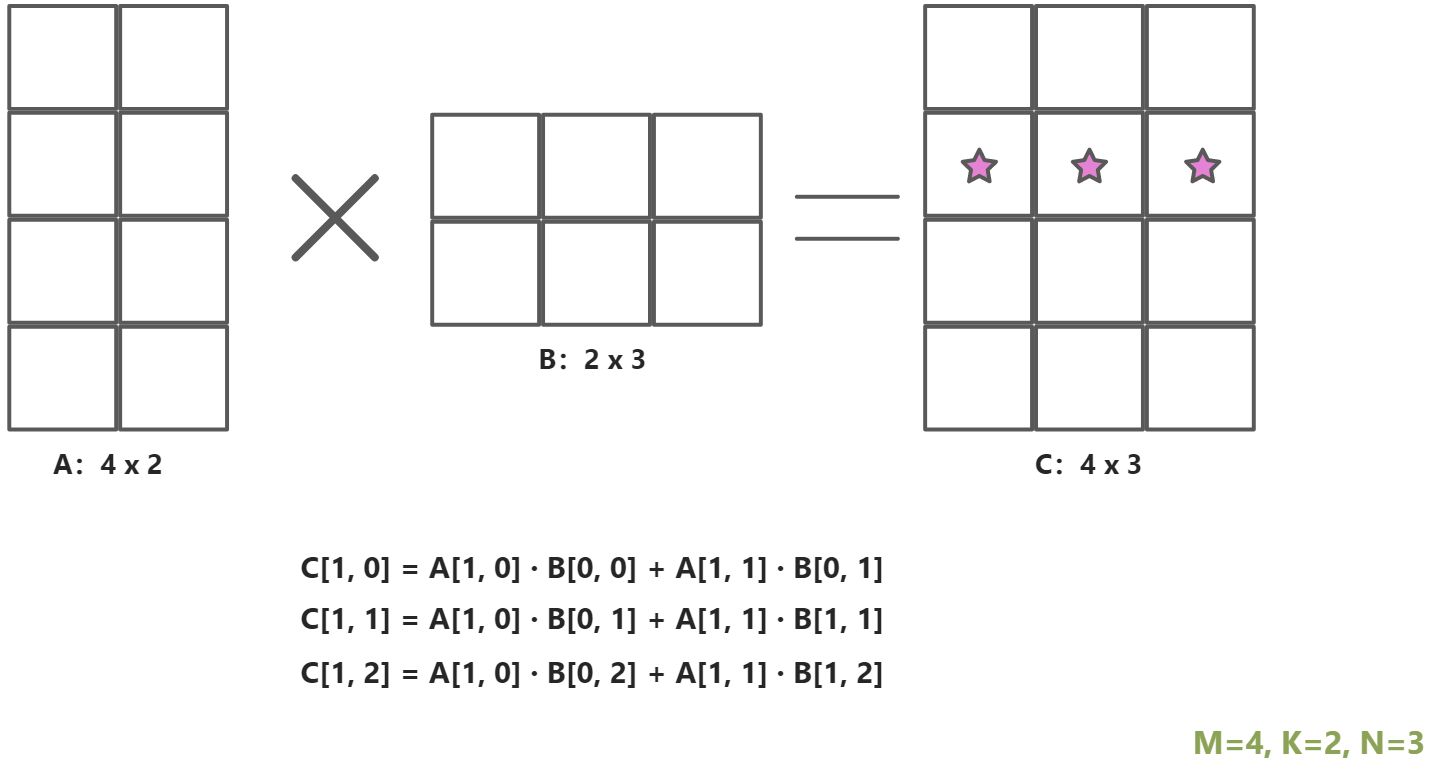
基础矩阵乘法，计算得到C矩阵，我们尝试要找出其计算瓶颈

1. 从上图中看出，计算C中的一行，都需要A的一行，以及B的每一列（总数N，整个矩阵B都会被加载）；计算C中的一列，都需要B的某一列，以及A的每一行（总数M，整个A都会被加载）。所以得到基本矩阵乘法的结果，计算C中的每一行，要加载B中的每一列M次；计算C中的每一列，都要加载A中的每一行N次。
2. 而且，每次计算C中的每一个元素都需要读取2k个元素。

之前的每次计算都只得到了C矩阵中的一个元素，现在我们的升级版本代码，会计算得到C矩阵中的一个方块区域内的元素。
平铺矩阵乘法
将内核的执行分解为多个阶段，将每个阶段的数据存放到共享内存中，使每个阶段的数据访问集中在一个子集上。
将大矩阵乘法分解为矩阵块乘法。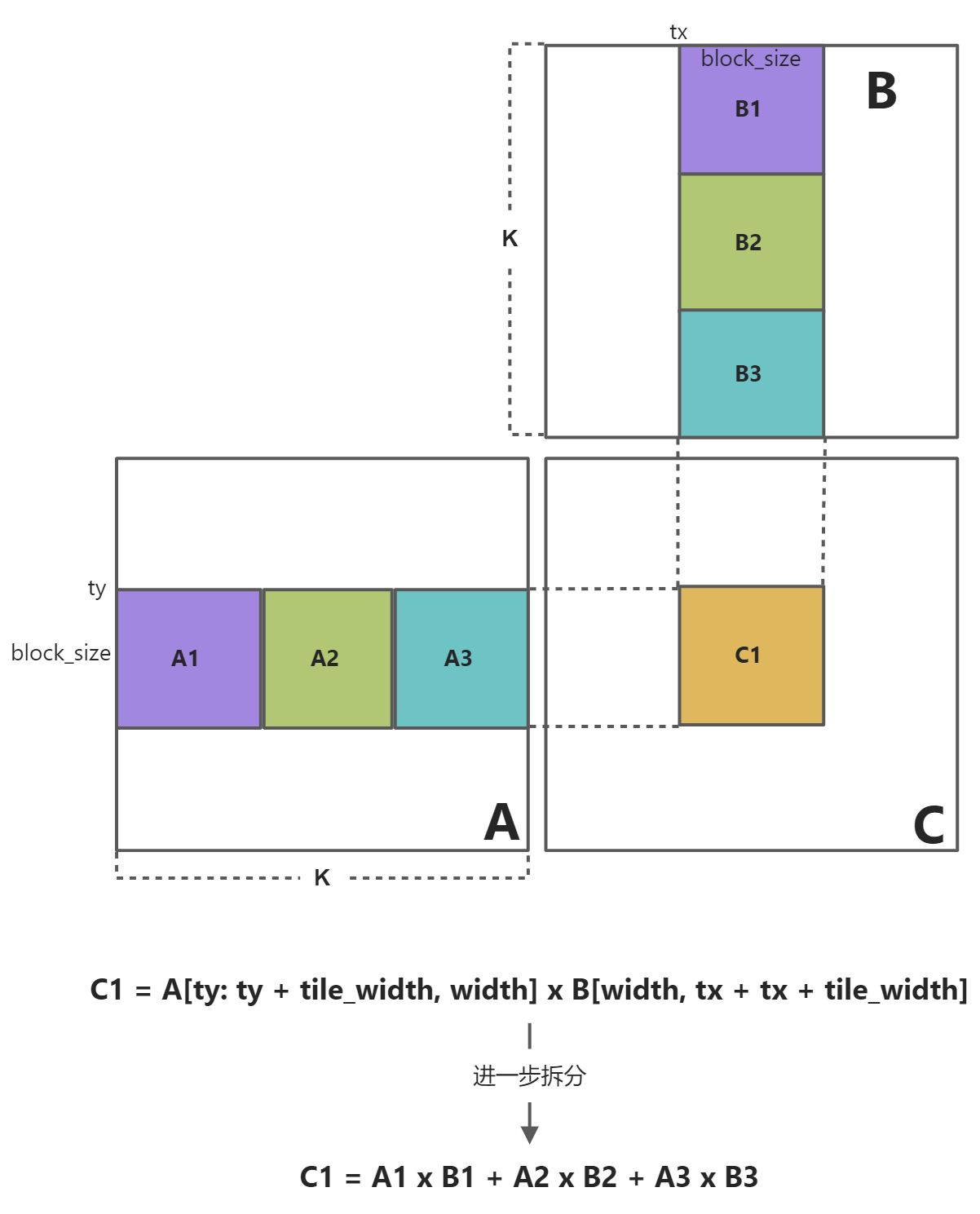

C1的大小为，为了计算C1的内容，先紫色部分放入到共享内存中，此时需要读取次内容，我们需要读取个block。所以，综上，共需要读取次内容。

对于基础矩阵相乘而言，计算C1时，需要读取次内容。

第一个平铺矩阵元素

• A1: [0: K/block_size, ty: ty + block_size]
• B1: [tx: tx + block_size, 0: K/block_size]

下一个平铺矩阵元素

• A2: [K/block_size: 2K/block_size, ty: ty + block_size]
• B2: [tx: tx + block_size, K/block_size: 2K/block_size]

  代码实现

  ```cpp global void matrixMul(Agpu,Bgpu,Cgpu,K){ _shared float A_tile(blockDim.y, blockDim.x) // 静态申请共享内存，存放A1 __shared float B_tile(blockDim.x, blockDim.y) accu <= 0 // core part / Accumulate C tile by tile. / // Row i of matrix C i <= blockIdx.y blockDim.y + threadIdx.y // Column j of matrix C j <= blockIdx.x blockDim.x + threadIdx.x // Store accumulated value to C(i,j) C_gpu(i,j) <= accu }

/ Accumulate C tile by tile. / for tileIdx = 0 to (K/blockDim.x - 1) do // 计算需要使用多少平铺矩阵 / Load one tile of A and one tile of B into shared mem / i <= blockIdx.y blockDim.y + threadIdx.y // Row i of matrix A j <= tileIdx blockDim.x + threadIdx.x // Column j of matrix B

// 将全局内存中的A1、B1 存放到共享内存中。
A_tile(threadIdx.y, threadIdx.x) <= A_gpu(i,j) // Load A(i,j) to shared mem
B_tile(threadIdx.x, threadIdx.y) <= B_gpu(j,i) // Load B(j,i) to shared mem
__sync() // Synchronize before computation
/* Accumulate one tile of C from tiles of A and B in shared mem */
for k = 0 to threadDim.x do
    accu <= accu + A_tile(threadIdx.y,k) * B_tile(k,threadIdx.x)
end
__sync()

end

```cpp
// nvcc -lcudart -lcublas matrixMultiple.cu -o MatrixMutipleGPU && ./MatrixMutipleGPU 
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>

#include "cuda_runtime.h"
#include "device_launch_parameters.h"
#include "cublas_v2.h"

#define M 512
#define K 512
#define N 512

#define BLOCK_SIZE 32 // block size ,each thread to calucate each bloc

void initial(float *array, int size)
{
    for (int i = 0; i < size; i++)
    {
        array[i] = (float)(rand() % 10 + 1);
    }
}

void printMatrix(float *array, int row, int col)
{
    float *p = array;
    for (int y = 0; y < row; y++)
    {
        for (int x = 0; x < col; x++)
        {
            printf("%10lf", p[x]);
        }
        p = p + col;
        printf("\n");
    }
    return;
}

void multiplicateMatrixOnHost(float *array_A, float *array_B, float *array_C, int M_p, int K_p, int N_p)
{
    for (int i = 0; i < M_p; i++)
    {
        for (int j = 0; j < N_p; j++)
        {
            float sum = 0;
            for (int k = 0; k < K_p; k++)
            {
                sum += array_A[i * K_p + k] * array_B[k * N_p + j];
            }
            array_C[i * N_p + j] = sum;
        }
    }
}

__global__ void multiplicateMatrixOnDevice(float *array_A, float *array_B, float *array_C, int M_p, int K_p, int N_p)
{
    int ix = threadIdx.x + blockDim.x * blockIdx.x; // row number
    int iy = threadIdx.y + blockDim.y * blockIdx.y; // col number

    if (ix < N_p && iy < M_p)
    {
        float sum = 0;
        for (int k = 0; k < K_p; k++)
        {
            sum += array_A[iy * K_p + k] * array_B[k * N_p + ix];
        }
        array_C[iy * N_p + ix] = sum;
    }
}

// Compute C = A * B
__global__ void matrixMultiplyShared(float *A, float *B, float *C,
                                     int numARows, int numAColumns, int numBRows, int numBColumns, int numCRows, int numCColumns)
{
    //@@ Insert code to implement matrix multiplication here
    //@@ You have to use shared memory for this MP

    __shared__ float sharedM[BLOCK_SIZE][BLOCK_SIZE];
    __shared__ float sharedN[BLOCK_SIZE][BLOCK_SIZE];

    int bx = blockIdx.x;
    int by = blockIdx.y;
    int tx = threadIdx.x;
    int ty = threadIdx.y;

    int row = by * BLOCK_SIZE + ty;
    int col = bx * BLOCK_SIZE + tx;

    float Csub = 0.0;

    for (int i = 0; i < (int)(ceil((float)numAColumns / BLOCK_SIZE)); i++)
    {
        // printf("block.x=%d,block.y=%d,threadIdx.x=%d,threadIdx.y=%d,row=%d,col=%d,sharedM[%d][%d]=A[%d],A的值：%f,sharedN[%d][%d]=B[%d],B的值：%f\n",
        //    blockIdx.x, blockIdx.y, threadIdx.x, threadIdx.y, row, col,
        //    threadIdx.y, threadIdx.x, row*numAColumns + i * BLOCK_SIZE + tx, A[row*numAColumns + i * BLOCK_SIZE + tx],
        //    threadIdx.y, threadIdx.x, (i*BLOCK_SIZE + ty)*numBColumns + col, B[(i*BLOCK_SIZE + ty)*numBColumns + col]);

        if (i * BLOCK_SIZE + tx < numAColumns && row < numARows)
            sharedM[ty][tx] = A[row * numAColumns + i * BLOCK_SIZE + tx];
        else
            sharedM[ty][tx] = 0.0;

        if (i * BLOCK_SIZE + ty < numBRows && col < numBColumns)
            sharedN[ty][tx] = B[(i * BLOCK_SIZE + ty) * numBColumns + col];
        else
            sharedN[ty][tx] = 0.0;
        __syncthreads();

        for (int j = 0; j < BLOCK_SIZE; j++)
            Csub += sharedM[ty][j] * sharedN[j][tx];
        __syncthreads();
    }

    if (row < numCRows && col < numCColumns)
        C[row * numCColumns + col] = Csub;
}

int main(int argc, char **argv)
{
    clock_t start = 0, finish = 0;
    float time;

    int Axy = M * K;
    int Bxy = K * N;
    int Cxy = M * N;

    float *h_A, *h_B, *hostRef, *deviceRef;
    h_A = (float *)malloc(Axy * sizeof(float));
    h_B = (float *)malloc(Bxy * sizeof(float));

    int nBytes = M * N * sizeof(float);
    hostRef = (float *)malloc(Cxy * sizeof(float));
    deviceRef = (float *)malloc(Cxy * sizeof(float));

    initial(h_A, Axy);
    // printf("\n");
    // printf("Matrix_A: (%d×%d)\n", M, K);
    // printMatrix(h_A, M, K);
    initial(h_B, Bxy);
    // printf("Matrix_B: (%d×%d)\n", K, N);
    // printMatrix(h_B, K, N);

    start = clock();
    multiplicateMatrixOnHost(h_A, h_B, hostRef, M, K, N);
    finish = clock();
    time = (float)(finish - start) / CLOCKS_PER_SEC;

    printf("\n");
    printf("------------------------------------------------------------------------------------\n");
    printf("Computing matrix product using multiplicateMatrixOnHost \n");
    printf("------------------------------------------------------------------------------------\n");

    printf("Matrix_hostRef: (%d×%d)  CPU运行时间为：%lfs\n", M, N, time);
    // printMatrix(hostRef, M, N);

    float *d_A, *d_B, *d_C;
    cudaMalloc((void **)&d_A, Axy * sizeof(float));
    cudaMalloc((void **)&d_B, Bxy * sizeof(float));
    cudaMalloc((void **)&d_C, Cxy * sizeof(float));

    cudaMemcpy(d_A, h_A, Axy * sizeof(float), cudaMemcpyHostToDevice);
    cudaMemcpy(d_B, h_B, Bxy * sizeof(float), cudaMemcpyHostToDevice);

    printf("\n\n");
    printf("------------------------------------------------------------------------------------\n");
    printf("Computing matrix product using multiplicateMatrixOnDevice \n");
    printf("------------------------------------------------------------------------------------\n");

    int dimx = 2;
    int dimy = 2;
    dim3 block(dimx, dimy);
    dim3 grid((M + block.x - 1) / block.x, (N + block.y - 1) / block.y);
    //      dim3 grid(1, 1);

    cudaEvent_t gpustart, gpustop;
    float elapsedTime = 0.0;
    cudaEventCreate(&gpustart);
    cudaEventCreate(&gpustop);
    cudaEventRecord(gpustart, 0);
    multiplicateMatrixOnDevice<<<grid, block>>>(d_A, d_B, d_C, M, K, N);
    cudaDeviceSynchronize();
    cudaEventRecord(gpustop, 0);
    cudaEventSynchronize(gpustop);

    cudaEventElapsedTime(&elapsedTime, gpustart, gpustop);
    cudaEventDestroy(gpustart);
    cudaEventDestroy(gpustop);

    cudaMemcpy(deviceRef, d_C, Cxy * sizeof(float), cudaMemcpyDeviceToHost);
    printf("Matrix_deviceRef: (%d×%d)  <<<(%d,%d),(%d,%d)>>>  GPU运行时间为：%fs\n",
           M, N, grid.x, grid.y, block.x, block.y, elapsedTime / 1000);
    // printMatrix(deviceRef, M, N);

    elapsedTime = 0.0;
    cudaEventCreate(&gpustart);
    cudaEventCreate(&gpustop);
    cudaEventRecord(gpustart, 0);
    matrixMultiplyShared<<<grid, block>>>(d_A, d_B, d_C, M, K, K, N, M, N);
    //    printf("   multiplicateMatrixOnDevice<<<(%d,%d),(%d,%d)>>>", grid.x, grid.y, block.x, block.y);
    cudaDeviceSynchronize();
    cudaEventRecord(gpustop, 0);
    cudaEventSynchronize(gpustop);

    cudaEventElapsedTime(&elapsedTime, gpustart, gpustop);
    cudaEventDestroy(gpustart);
    cudaEventDestroy(gpustop);

    cudaMemcpy(deviceRef, d_C, Cxy * sizeof(float), cudaMemcpyDeviceToHost);
    printf("Matrix_deviceRef: (%d×%d)  <<<(%d,%d),(%d,%d)>>>  GPU运行时间为：%fs\n",
           M, N, grid.x, grid.y, block.x, block.y, elapsedTime / 1000);
    // printMatrix(deviceRef, M, N);
    /*
            elapsedTime = 0.0;
            cudaEventCreate(&gpustart);
            cudaEventCreate(&gpustop);
            cudaEventRecord(gpustart, 0);
    */
    cublasStatus_t status;
    cublasHandle_t handle;
    cublasCreate(&handle);

    elapsedTime = 0.0;
    cudaEventCreate(&gpustart);
    cudaEventCreate(&gpustop);
    cudaEventRecord(gpustart, 0);

    float a = 1, b = 0;
    cublasSgemm(
        handle,
        CUBLAS_OP_T, //矩阵A的属性参数，转置，按行优先
        CUBLAS_OP_T, //矩阵B的属性参数，转置，按行优先
        M,             //矩阵A、C的行数
        N,             //矩阵B、C的列数
        K,             // A的列数，B的行数，此处也可为B_ROW,一样的
        &a,             // alpha的值
        d_A,         //左矩阵，为A
        K,             // A的leading dimension，此时选择转置，按行优先，则leading dimension为A的列数
        d_B,         //右矩阵，为B
        N,             // B的leading dimension，此时选择转置，按行优先，则leading dimension为B的列数
        &b,             // beta的值
        d_C,         //结果矩阵C
        M             // C的leading dimension，C矩阵一定按列优先，则leading dimension为C的行数
    );
    cudaMemcpy(deviceRef, d_C, Cxy * sizeof(float), cudaMemcpyDeviceToHost);
    cudaDeviceSynchronize();
    cudaEventRecord(gpustop, 0);
    cudaEventSynchronize(gpustop);

    cudaEventElapsedTime(&elapsedTime, gpustart, gpustop);
    cudaEventDestroy(gpustart);
    cudaEventDestroy(gpustop);

    printf("Matrix_deviceRef: (%d×%d)  <<<(%d,%d),(%d,%d)>>>  GPU运行时间为：%fs\n",
           M, N, grid.x, grid.y, block.x, block.y, elapsedTime / 1000);

    cudaFree(d_A);
    cudaFree(d_B);
    cudaFree(d_C);

    free(h_A);
    free(h_B);
    free(hostRef);
    free(deviceRef);

    cudaDeviceReset();

    return (0);
}

总结

• 基础矩阵乘法，会从全局内存中取次
• 平铺矩阵乘法，会从全局内存中取
• 理论加速比：
• 实际情况中，会有同步函数和共享内存读写等操作，实际加速比要低。