2.3 Floating point Numbers

#include <iostream>
#include <iomanip>
using namespace std;
int main()
{
    float f1 = 1.2f;
    float f2 = f1 * 1000000000000000; //1.0e15
    cout << std::fixed << std::setprecision(15) << f1 << endl;
    cout << std::fixed << std::setprecision(15) << f2 << endl;
    return 0;
}
// 1.200000047683716
// 1200000038076416.000000000000000

可以看到输出结果并不是真正的1.2，结果都会有很小的误差，为什么？

• Q1: How many numbers in range [0, 1]? [0, 1]之间有多少实数。
  • A1: Infinite! 无穷多个
• Q2：How many numbers can 32 bits represent?
  • A2：只能表示个数字，实际也没多大，也就4GB

这就有个大问题：无穷多的数值如何只用32位去表达？unposible
You want 1.2, but float can only provide you 1.200000047683716…

• Are computers always accurate?
  • Floating-point operations always bring some tiny errors.
  • Those errors cannot be eliminated. 浮点数运算会带来微小的误差，无法避免
• What we can do: to manage them not to cause a problem.

float: single precision floating-point type, 32 bits
float：单精度浮点数，32位

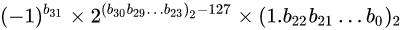
第一位是符号位

double: double precision floating-point type, 64 bits 双精度浮点数，64位
long double: extended precision floating-point type

• 128 bits if supported
• 64 bits otherwise

half precision floating-point, 16 bits, (used in deep learning, but not a C++ standard)

Floating-point VS integers

• Represent values between integers, 表示小数
• A much greater range of values，表示范围大
• Floating-point operations are slower than integer operations，float操作要比int操作慢
• Lose precision
  • 对于int32 位和float32位来说，float32表达范围更广，你可能准确的表达所有的点，意味着只能采样选取具有代表性的点来表达当前值，是个近似值，所以精度比int低
• double operations is slower than float，double类型要比float还要慢

精度问题

#include <iostream>
using namespace std;
int main()
{
    float f1 = 2.34E+10f;
    float f2 = f1 + 10;   // but f2 = f1
    cout.setf(ios_base::fixed, ios_base::floatfield); // fixed-point
    cout << "f1 = " << f1 << endl;
    cout << "f2 = " << f2 << endl;
    cout << "f1 - f2 = " << f1 - f2 << endl;
    cout << "(f1 - f2 == 0) = " << (f1 - f2 == 0) << endl;
    return 0;
}

Will f2 be greater than f1?

// result
f1 = 23399999488.000000
f2 = 23399999488.000000
f1 - f2 = 0.000000
(f1 - f2 == 0) = 1

f1的值是个近似的量，且f1和f2结果相同，两者相减结果为0。WHY？？？

• 其采样精度不够，浮点类型是间隔性采样，加10之后，达不到采样下一个点的位置，还是离f1的值的更近，所以还是近似之后等于f1。如果加100，如果超出了间隔，采样得到的新值就会变化。
• 所以还是浮点类型的表达精度问题，编程时要格外小心。

判断两个浮点数是否相等，最好不要用==操作符，
Can we use == operator to compare two floating point numbers?

if (f1 == f2) //bad
if (fabs(f1 - f2) < FLT_EPSILON) // good

inf and nan：无穷值和not a number

#include <iostream>
using namespace std;

int main()
{
    float f1 = 2.0f / 0.0f;
    float f2 = 0.0f / 0.0f;
    cout << f1 << endl;
    cout << f2 << endl;
    return 0;
}

• ±inf: infinity (Exponent=11111111, fraction=0)
• nan: not a number (Exponent=11111111, fraction!=0)