模型原理与应用

定义

元胞自动机(cellular automata)是一种时间、空间、状态都离散，空间相互作用和时间因果关系为局部的网格动力学模型，具有模拟复杂系统时空演化过程的能力。
元胞自动机是离散的动力学系统：

离散的系统：元胞是定义在有限的时间和空间上的，并且元胞状态是有限的。
动力学系统：元胞自动机的举止行为具有动力学特征。
简单与复杂：元胞自动机用简单规则控制相互作用的元胞模拟复杂世界。

构成要素
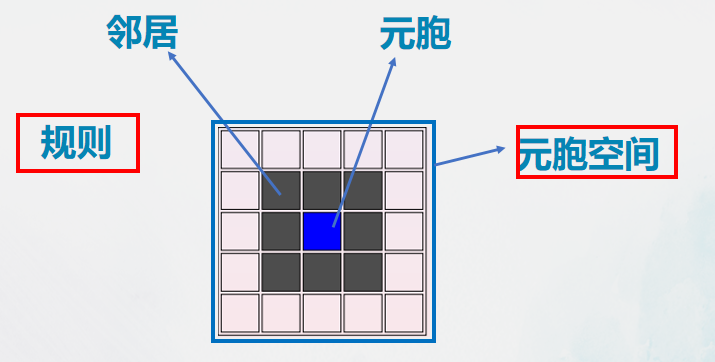
元胞自动机由元胞、元胞空间、元胞邻居和元胞规则四部分组成。

元胞
元胞是元胞自动机基本单元：
状态：每个元胞都有记忆储存状态的功能。
离散：简单情况下，元胞只有两种可能状态；较复杂情况下，元胞具有多种状态。
更新：元胞的状态都按照动力规则不断更新。
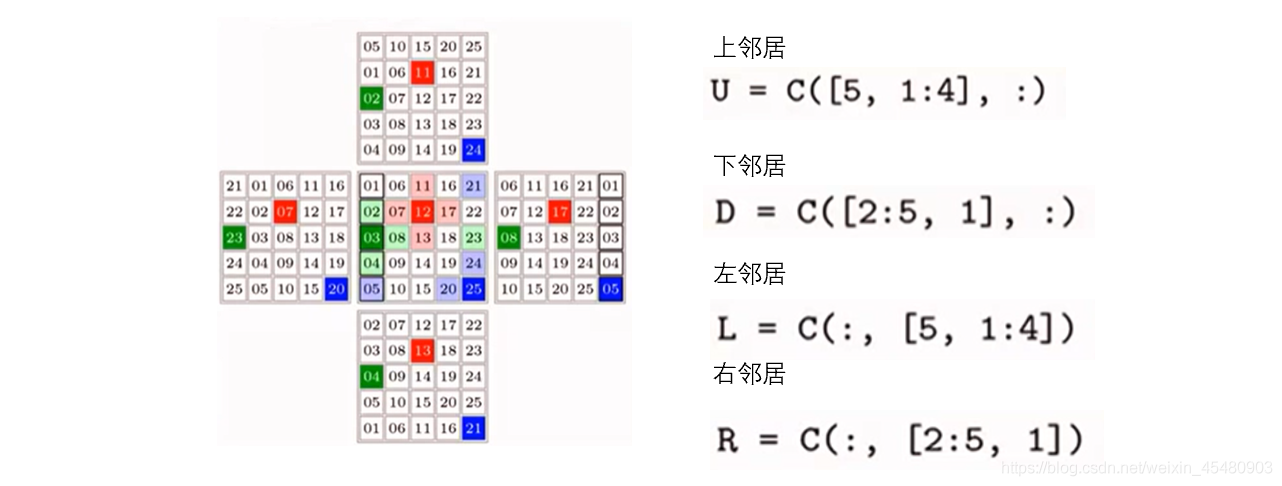
邻居
对邻居的理解并不固定，通常来说的邻居便是指冯诺伊曼型。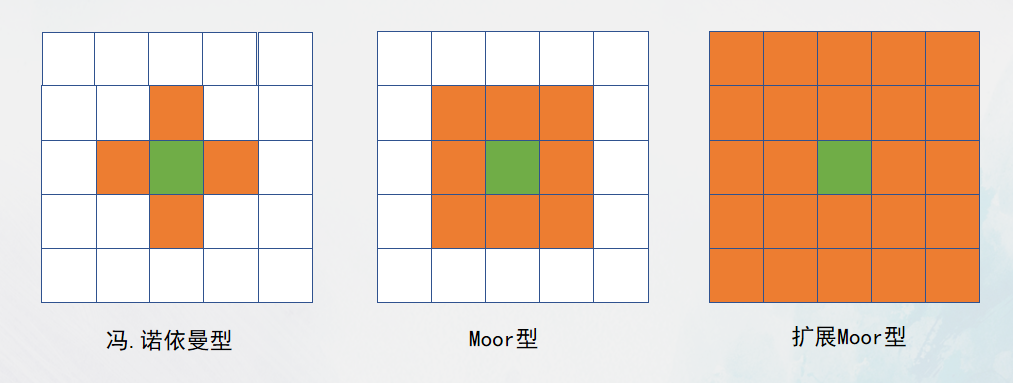

边界条件
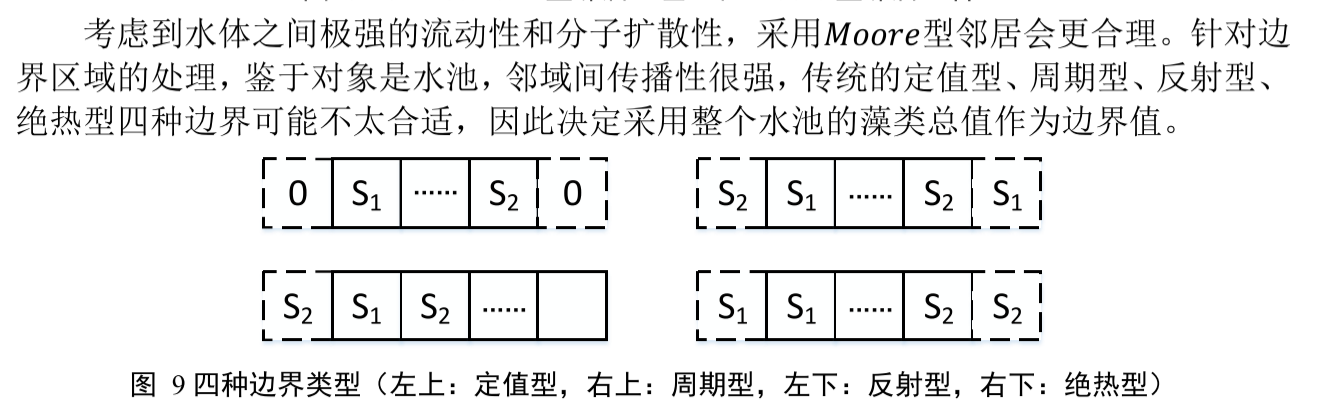
理论上，元胞空间是无限的，实际应用中无法达到这一理想条件。为了给元胞空间边界上的元胞拥有规则所需要的邻居，就需要构造出一些虚拟的邻居。
固定型边界
固定型：在边界部分指定一个数。
周期型边界
周期型，将最右侧的邻居当作虚拟的左侧。

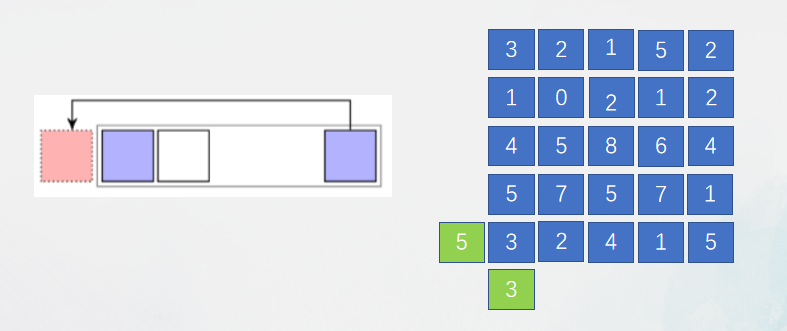
绝热型边界
绝热型：自己是自己的邻居。

映射型边界
映射型：以自己为中心进行对称。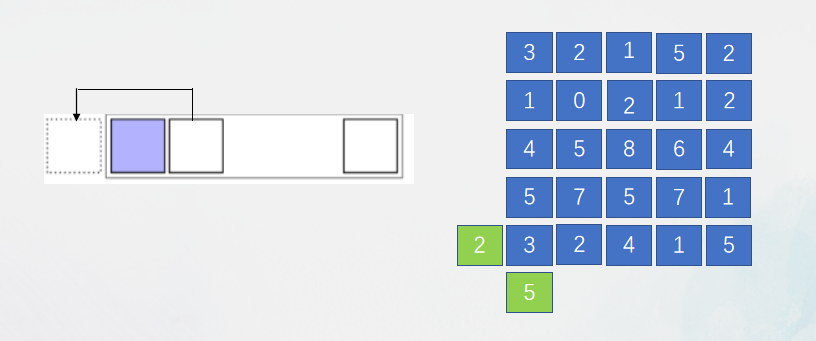

规则（状态转移函数）
根据元胞当前状态及邻居的状态来决定下一时刻该元胞状态。元胞自动机根据规则进行局部元胞间的相互作用从而引起全局的变化。
规则可以多种多样，比如围棋中，被包围的棋子状态由黑/白转为空，即一种规则。
应用

社会学：元胞自动机经常用于研究个人行为的社会性，流行现象，例如人口迁移，公共场所内人员的疏散，流行病传播。
图形学：元胞自动机以其特有的结构的简单性，内在的并行性以及复杂计算的能力成为密码学中研究的热点方向之一。

物理学：在物理学中，元胞自动机已成功的应用于流体，磁场，电场，热传导等的模拟，例如格子气自动机。

例子：火灾模拟

元胞有3个不同的状态。状态为0是树木，状态= 1是空地，状态= 5是燃烧着的树木。
如果4个邻居中有一个或一个以上的是燃烧着的并且自身是树木，那么该元胞下一时刻的状态是燃烧。
森林元胞(状态为0 )以一个低概率(例如0.000005 )开始烧(因为闪电)。
一个燃烧着的元胞(状态为5 )在下一时刻(时间步长可以控制)变成空位的（状态为0）。
空元胞以一一个低概率（例如0.01 ）变为森林以模拟生长。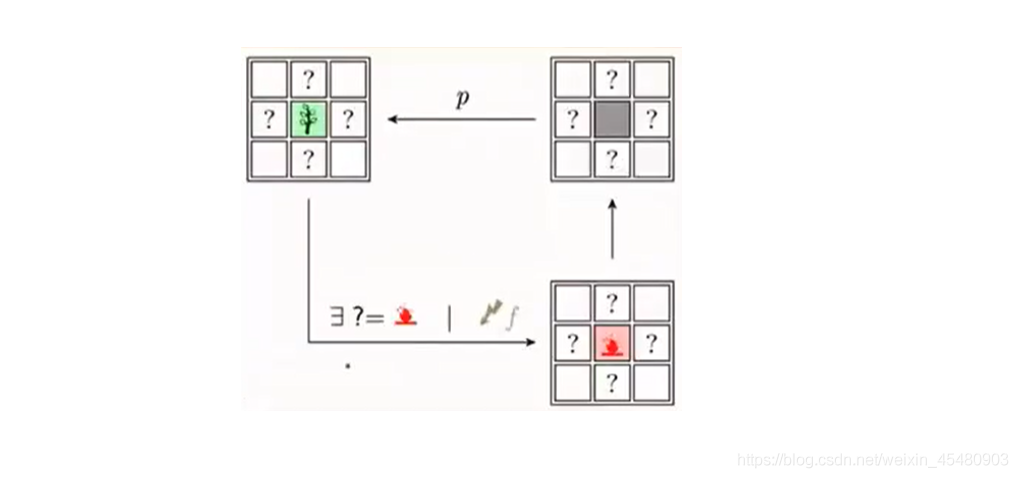

通过理论分析，得出以下公式：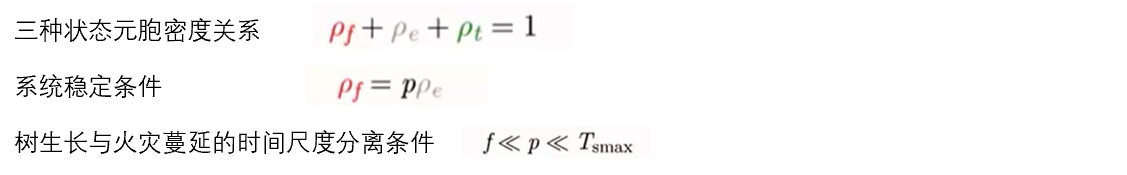

clc；
clear；
n = 300;                           % 定义表示森林的矩阵大小
Plight = 5e-6; Pgrowth = 1e-2;     % 定义闪电和生长的概率  
UL = [n,1:n-1]; DR = [2:n,1];      % 定义上左，下右邻居
veg=zeros(n,n);                    % 初始化表示森林的矩阵
imh = image(cat(3,veg,veg,veg));   % 可视化表示森林的矩阵
% veg = 空地为0 着火为1 树木为2
for i=1:3000 
 sum =(veg(UL,:)==1) + (veg(:,UL)==1)+(veg(:,DR)==1) +  (veg(DR,:)==1);  % 计算出所有格子有几个邻居是着火的
% 根据规则更新森林矩阵：是否树=是否树-是否着火的树+是否新生的树（0-1运算）
 veg = 2*(veg==2) - ( (veg==2) & (sum>0 |(rand(n,n)<Plight)) ) +2*((veg==0) & rand(n,n)<Pgrowth) ;  
 set(imh, 'cdata', cat(3,(veg==1),(veg==2),zeros(n)) )
 drawnow                         % 可视化表示森林的矩阵
end