一、概述

（1）什么是数学规划？
数学规划是运筹学的一个分支，用来研究在给定条件下（约束条件），如何按照某一衡量指标（目标函数）来寻求计划、管理工作中的最优方案。=>求目标函数在一定约束条件下的极值问题。例如高考试卷中的线性规划大题。
（2）数学规划的分类

  • 线性规划

如果目标函数和约束条件均是决策变量的线性表达式，那么此时的数学规划问题就属于线性规划。

  • 非线性规划

当目标函数或者约束条件中有一个是决策变量x的非线性表达式，那么此时的数学规划问题就属于非线性规划。

  • 整数规划

    整数规划是一类要求变量取整数值的数学规划：目前所流行的整数规划的算法往往只适用于线性整数规划。

  • 0-1规划：整数规划的特例，整数变量的取值只能是0和1

    二、线性规划问题的求解

    1.matlab中线性规划的标准型
    image.png
    2.matlab中求解线性规划的函数
    image.png

    2.1 生产决策问题

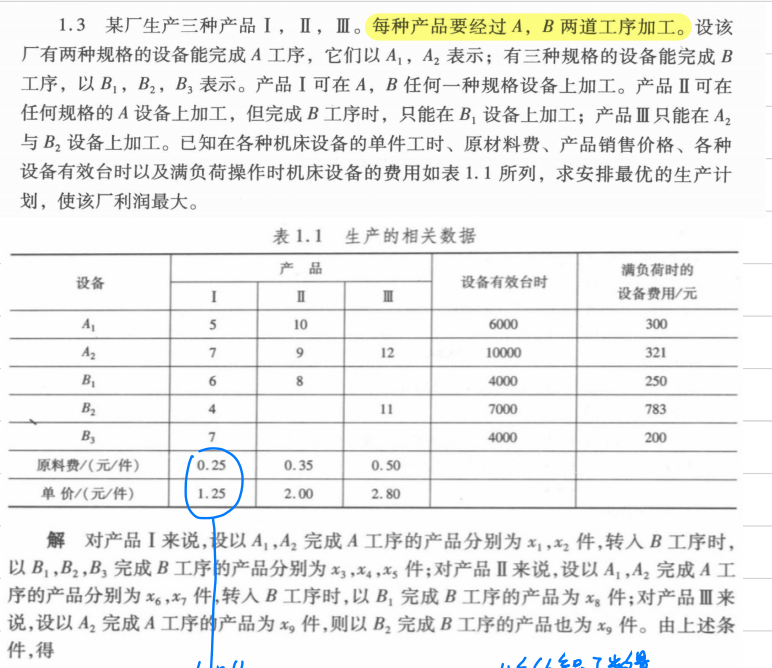    image.png ```matlab %% 生产决策问题 format long g %可以将Matlab的计算结果显示为一般的长数字格式（默认会保留四位小数，或使用科学计数法） % (1) 系数向量 c = zeros(9,1); % 初始化目标函数的系数向量全为0 c(1) = 1.25 -0.25 -300/60005; % x1前面的系数是c1 c(2) = 1.25 -0.25 -321/100007; c(3) = -250 / 4000 6; c(4) = -783/70004; c(5) = -200/4000 7; c(6) = -300/600010; c(7) = -321 / 10000 9; c(8) = 2-0.35-250/40008; c(9) = 2.8-0.5-321/1000012-783/700011; c = -c; % 我们求的是最大值，所以这里需要改变符号 % (2) 不等式约束 A = zeros(5,9); A(1,1) = 5; A(1,6) = 10; A(2,2) = 7; A(2,7) = 9; A(2,9) = 12; A(3,3) = 6; A(3,8) = 8; A(4,4) = 4; A(4,9) = 11; A(5,5) = 7;
    b = [6000 10000 4000 7000 4000]’; % (3) 等式约束 Aeq = [1 1 -1 -1 -1 0 0 0 0; 0 0 0 0 0 1 1 -1 0]; beq = [0 0]’; %（4）上下界 lb = zeros(9,1);

% 进行求解 [x fval] = linprog(c, A, b, Aeq, beq, lb) fval = -fval % fval = % 1146.56650246305 % 注意，本题应该是一个整数规划的例子，我们在后面的整数规划部分再来重新求解。 intcon = 1:9; [x,fval]=intlinprog(c,intcon,A,b,Aeq,beq,lb) fval = -fval

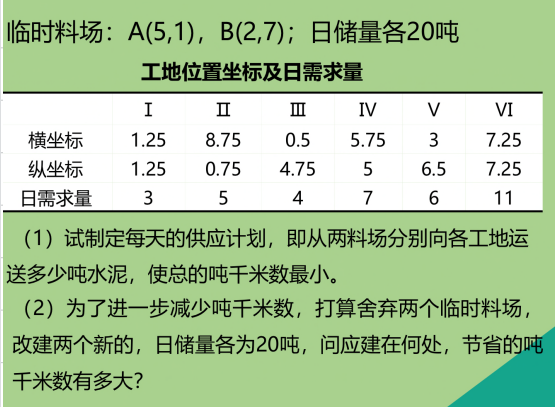
  1. <a name="Zpo01"></a>
  2. #### 2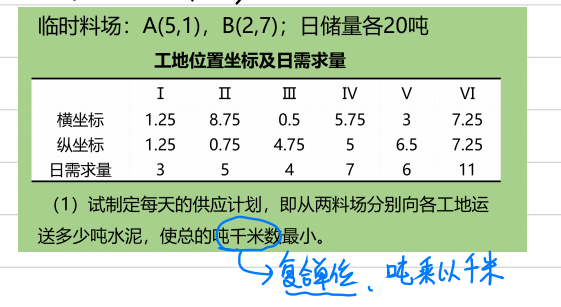.2 投料问题
  3. ![image.png](https://cdn.nlark.com/yuque/0/2022/png/28834230/1655518143786-8e9ff62c-40b8-42c0-ad4e-c1277be7bdb4.png#clientId=uda071891-5fec-4&crop=0&crop=0&crop=1&crop=1&from=paste&height=246&id=u1a765e53&margin=%5Bobject%20Object%5D&name=image.png&originHeight=307&originWidth=561&originalType=binary&ratio=1&rotation=0&showTitle=false&size=83204&status=done&style=none&taskId=u7f610555-276a-4eb7-bbac-b418bcacb2c&title=&width=448.8)
  4. ```matlab
  5. %% 投料问题
  6. clear,clc
  7. format long g   %可以将Matlab的计算结果显示为一般的长数字格式（默认会保留四位小数，或使用科学计数法）
  8. % (1) 系数向量
  9. a=[1.25  8.75  0.5  5.75  3  7.25];  % 工地的横坐标
  10. b=[1.25  0.75  4.75    5  6.5  7.25];   % 工地的纵坐标
  11. x = [5  2];  % 料场的横坐标
  12. y = [1  7];  % 料场的纵坐标
  13. c = [];  % 初始化用来保存工地和料场距离的向量 (这个向量就是我们的系数向量）
  14. for  j =1:2
  15.     for i = 1:6
  16.         c = [c;  sqrt( (a(i)-x(j))^2 + (b(i)-y(j))^2)];  % 每循环一次就在c的末尾插入新的元素
  17.     end
  18. end
  19. % (2) 不等式约束
  20. A =zeros(2,12);
  21. A(1,1:6) = 1;
  22. A(2,7:12) = 1;
  23. b = [20,20]';
  24. % (3) 等式约束
  25. Aeq = zeros(6,12);  
  26. for i = 1:6
  27.     Aeq(i,i) = 1;  Aeq(i,i+6) = 1;
  28. end
  29. % Aeq = [eye(6),eye(6)]  % 两个单位矩阵横着拼起来
  30. beq = [3 5 4 7 6 11]';  % 每个工地的日需求量
  31. %（4）上下界
  32. lb = zeros(12,1);
  34. % 进行求解
  35. [x fval] = linprog(c, A, b, Aeq, beq, lb)
  36. x = reshape(x,6,2)  % 将x变为6行2列便于观察（reshape函数是按照列的顺序进行转换的，也就是第一列读完，读第二列，即x1对应x_1,1，x2对应x_2,1）
  38. % fval =
  39. %           135.281541790676

三、非线性规划问题的求解

1.matlab中非线性规划的标准型
image.png
2.matlab求解非线性规划的函数
image.png
image.png
image.png

3.1 选址问题

image.png

3.2 飞行管理问题

四、整数规划

image.png
1.matlab线性整数规划求解
image.png
2.matlab线性0-1规划求解
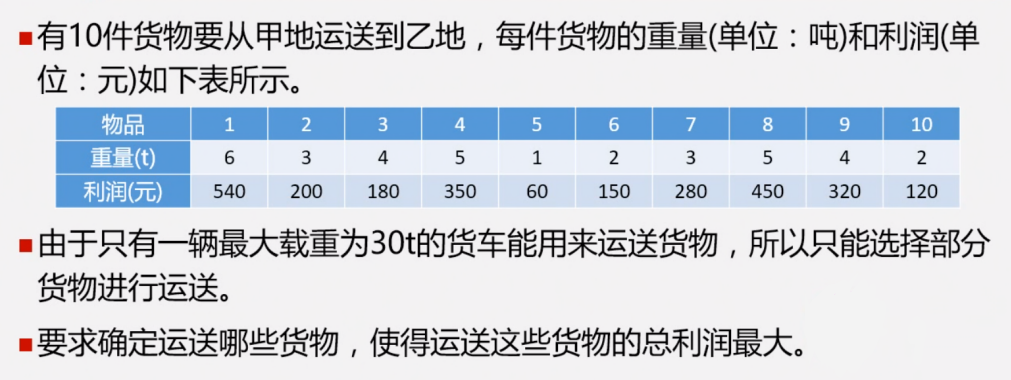
image.png

4.1 背包问题

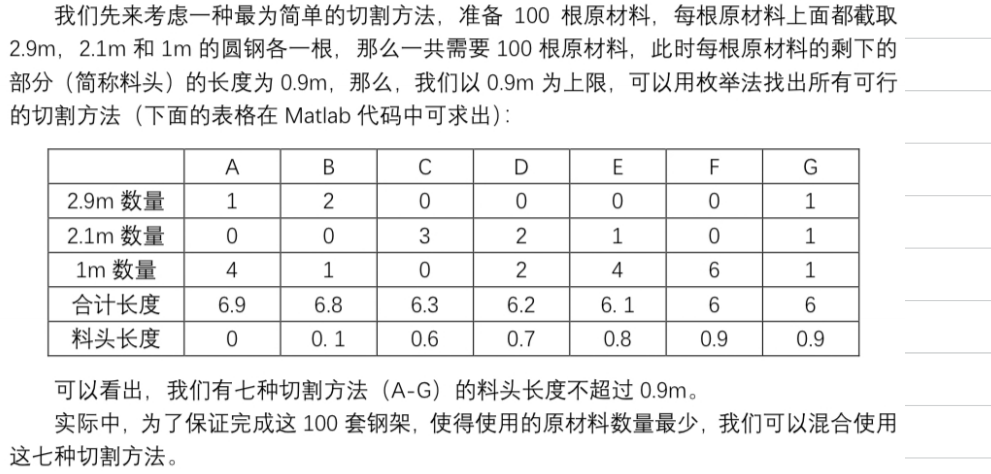
image.png
image.png

4.2 指派问题

image.png
image.png

4.3 钢管切割问题

image.png
image.png
image.png

五、最大最小化模型

image.png

六、多目标规划模型

求解思路

image.png