层次分析法

一、内容介绍

层次分析法是指将一个复杂的多目标决策问题作为一个系统，将目标分解为多个目标或准则，进而分解为多指标（或准则、约束）的若干层次，通过定性指标模糊量化方法算出层次单排序（权数）和总排序，以作为目标（多指标）、多方案优化决策的系统方法。
层次分析法是将决策问题按总目标、各层子目标、评价准则直至具体的备投方案的顺序分解为不同的层次结构，然后用求解判断矩阵特征向量的办法，求得每一层次的各元素对上一层次某元素的优先权重，最后再加权和的方法递阶归并各备择方案对总目标的最终权重，此最终权重最大者即为最优方案。
层次分析法比较适合于具有分层交错评价指标的目标系统，而且目标值又难于定量描述的决策问题。

二、具体过程

1.建立层次结构模型

将决策问题分成三个层次，最上层为目标层M，即×××；最下层为方案层，即×××；中间层为准则层，包括×××（如图所示）：

2.模型求解

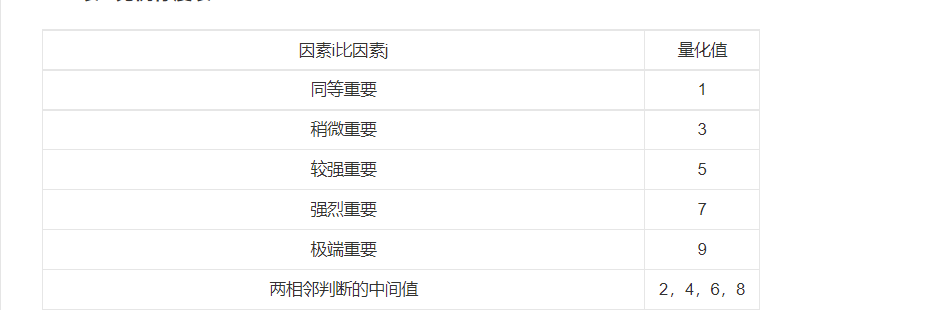
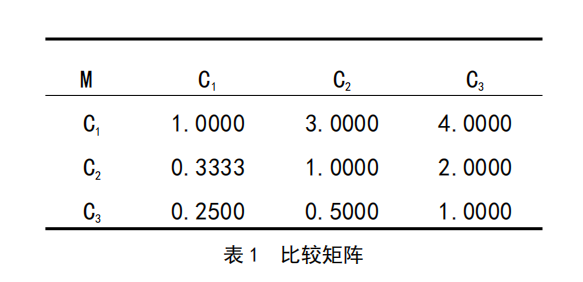
1.构造判断矩阵M-C：将准则层中三个元素C1,C2,C3两两比较，得成对比较矩阵(三线表)。

判断标准（论文中不用画这个表格）：

1.1求解特征值

1.2求解权重向量

1.3n与RI关系表

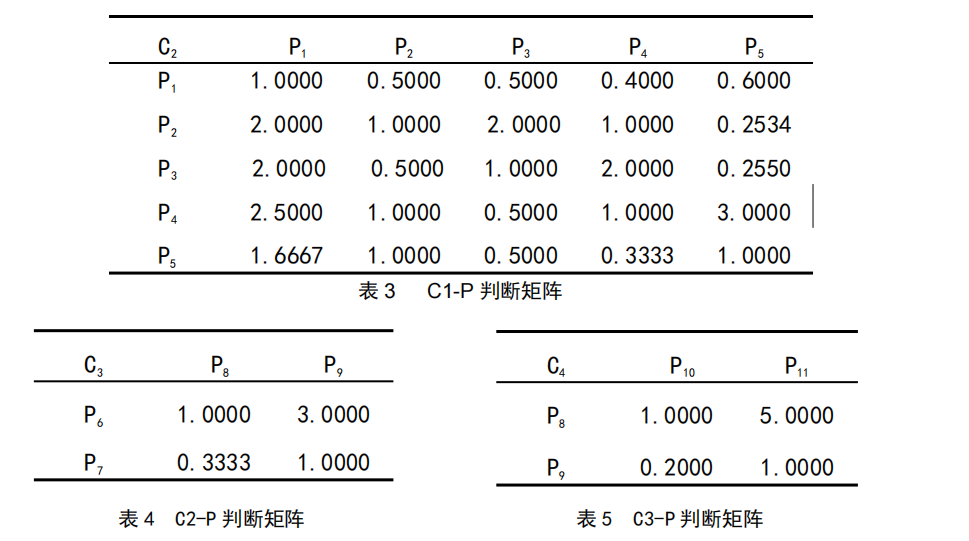
2.构造判断矩阵C1-P,C2-P,C3-P。(表格C的下标应该写错了…)

3.分层排序与总排序一致性检验

此处将以上判断矩阵数据导入到MATLAB中，分别得到各层的权重排序，并且进行判断矩阵一致性检验，经过对判断矩阵进行合理化调整后，各矩阵都具有一致性。具体MATLAB实现过程、代码见附录×、×。
将由上述的三个判断矩阵计算出的权重向量，最大特征值入i和一致性指标CRi列入表中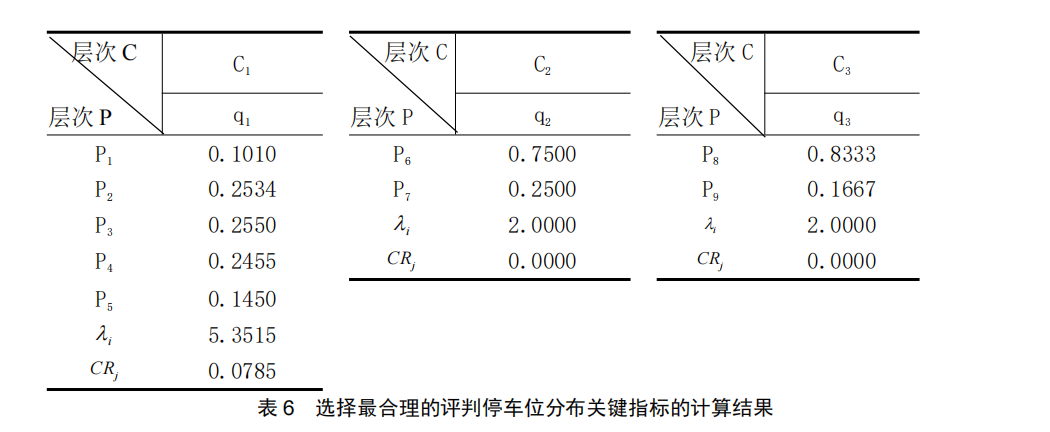

从表中CRj的值可以看出，矩阵C1-P,C2-P,C3-P都通过了一致性检验

二、模型结论与分析

计算出P层每个影响因素所占的总权重。将表格汇总成如下表格（比重可视化）：

三、结果分析

影响因素：

• 1. …
• 1. …
• 1. …

     四、层次分析法的评估

     优点：具有系统性、简洁实用性、所需定量数据信息较少，这种方法尤其可用于无结构特性的系统评价以及多目标、多准则、多时期等的系统评价，而且结果简单明确、可信度较高。然而，层次分析法虽然可以简单地把综合指标量化，但在权重的确定方面主观性太强
     ，因此通过构造出来的判断矩阵所求出来的权值不一定可靠从而不能客观的评价交通的影响指标。

     五、一些废话

• APH法将专家的经验判断给予量化，将大脑分析方案的思维过程图示化，可以简单、全面、清晰地处理由众多因素制约或缺乏必要数据的复杂问题。