基本原理、核心思想

蒙特卡洛方法（蒙特卡洛模拟）的核心思想是用计算机生成随机数来得到近似的最优解，其基本原理就是概率论中的大数定律，即当样本容量足够大时，事件的发生频率即为其概率。
蒙特卡洛准确的来说只是⼀种思想，或者是是⼀种⽅法。如果我们所求解的问题与概率模型有⼀定的关联，那么我们就可以使⽤计算机多次模拟事件发生，以获得问题的近似解。因此根据不同的问题，对应的约束条件以及算法模型不同，蒙特卡洛模拟的方法的代码没有通用的架构（根据题目条件写代码）。

应用场景一：利用蒙特卡洛方法求圆周率pi

特点：问题与概率模型显著关联（可以明确推导出问题的概率公式）

原理

场景模型建立：画一个边长为2R的正方形以及边长为R的内接圆，随机地向正方形区域内撒点，那么：
（落在圆内点的个数）/（落在正方形内点的个数）=（圆的面积）/（正方形的面积）=π/4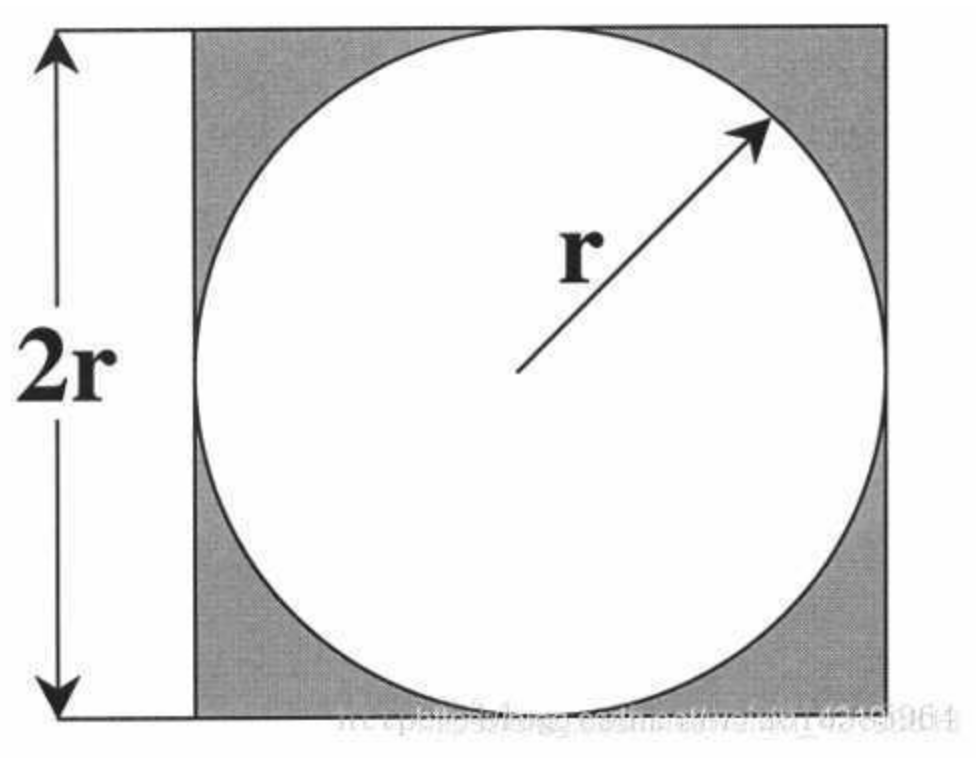

代码

%模拟次数
n=10000;
%unifrnd(a,b,m,n)可以输出在[a,b]之间均匀分布的随机数组成的m行n列的矩阵。
%分别生成点的x坐标和y坐标数组
points_x = unifrnd(-1,1,1,n);
points_y = unifrnd(-1,1,1,n);
%在圆内的点的数量
in_cycle=0;
%确定xy坐标轴范围，设置横坐标范围为[-1, 1] 纵坐标范围为[-1, 1]
axis([-1,1,-1,1]);
for k=1:n
    %通过距离原点距离来判断，随机生成的第k个点是否在圆内
    if points_x(k)^2+points_y(k)^2<=1
        in_cycle=in_cycle+1;
        %在圆内的点画红点，否则画蓝点
        plot(points_x(k),points_y(k),'r.');
        hold on;%不关闭图形，继续画图
    else
        plot(points_x(k),points_y(k),'b.');
        hold on;
    end
end
disp(['蒙特卡罗方法得到pi为：', num2str(4*(in_cycle/n))]);

实验结果

模拟结果图：

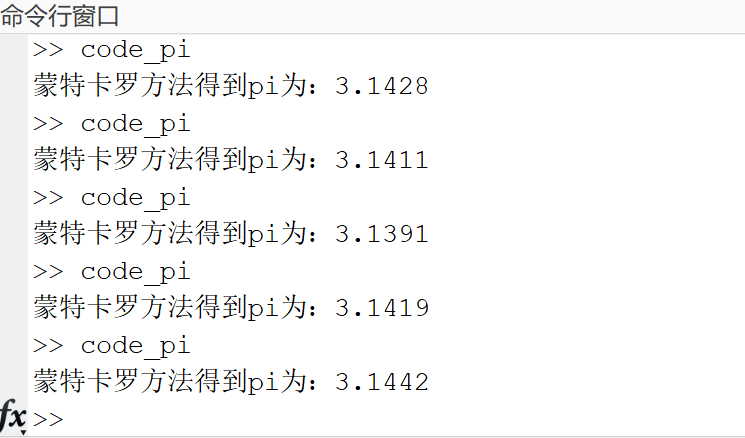
我们可以发现：多次实验的结果均接近π的值，即蒙特卡洛方法模拟出来的值是近似值，而不是最优值

论文应用一：模型近似结果的检验：

场景应用二：三门问题

场景描述：

你参加一档电视节目，节目组提供了ABC三扇门，主持人告诉你，其中一扇门后边有辆汽车，其它两扇门后是空的。
假如你选择了B门，这时，主持⼈打开了C门，让你看到C门后什么都没有，然后问你要不要改选A门？
论文应用二：

数学建模知识共享

蒙特卡洛方法