（相对于主成分分析，因子分析优先，可以用主成分分析就可以用因子分析）

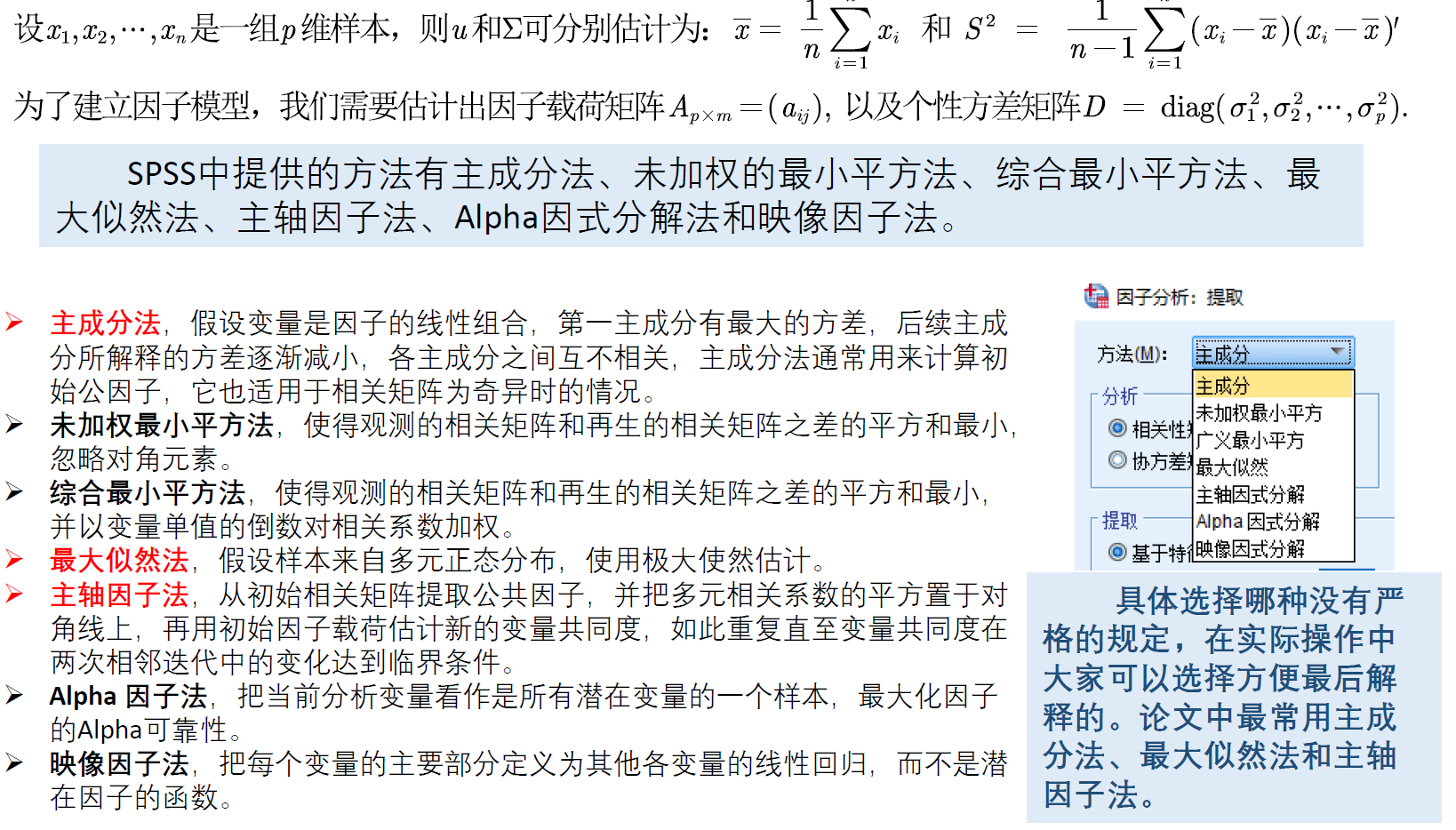
基本原理与用途

概述

因子分析法通过研究变量间的相关系数矩阵，把这些变量间错综复杂的关系归结成少数几个综合因子，由于归结出的因子个数少于原始变量的个数，但是它们又包含原始变量的信息，所以，这一分析过程也称为降维。由于因子往往比主成分更易得到解释，故因子分析比主成分分析更容易成功，从而有更广泛的应用。

因子分析和主成分分析的对比

image.png
其他主要区别：

  1. 主成分分析只是简单的数值计算，不需要构造一个模型，几乎没什么假定；而因子分析需要构造一个因子模型，并伴随几个关键性的假定。
  2. 主成分的解是唯一的，而因子可有许多解。因子解释成功的可能性要远大于主成分解释成功的可能性。

（简而言之，主成分分析是几个选取重要的指标，而因子分析选取几类重要指标（由原始指标线性组成））
（举例说明一下：image.png使用主成分分析，我可以得到诚实、交际能力等几个方面能力更重要；而使用因子分析我可以归纳为社交能力、经
验、讨人喜欢的程度、专业能力和外貌这五个因子）

模型介绍

因子分析原理

image.png

因子分析的假设

image.png

因子模型的性质

image.png
（因子载荷矩阵A不是唯一的，在实际的应用中我们常常利用这一点，通过因子的变换，使得新的因子具有更容易解释的实际意义。这就是因子分析往往比主成分分析的结果更容易解释的原因。）

因子载荷矩阵的统计意义

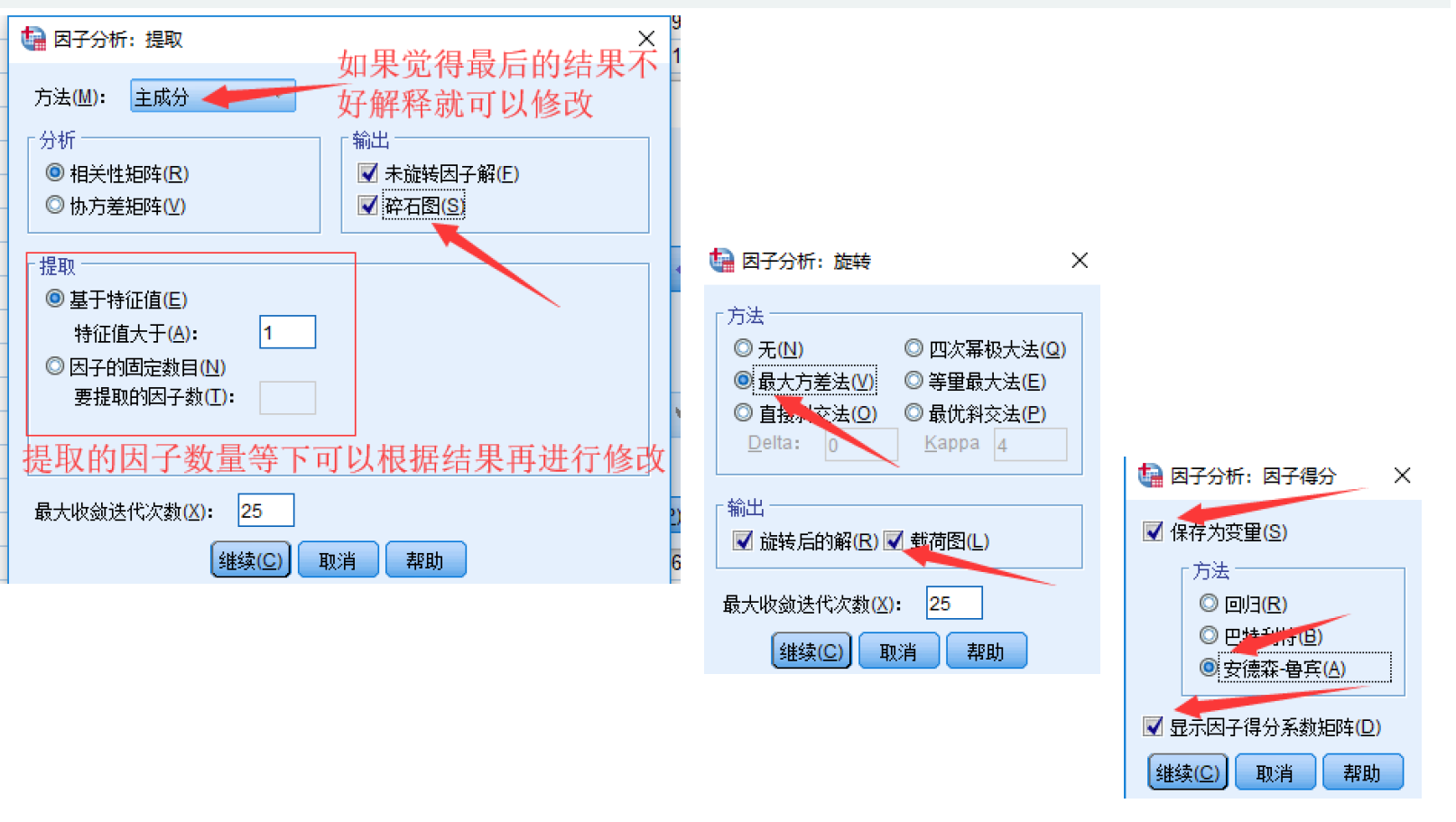
image.png
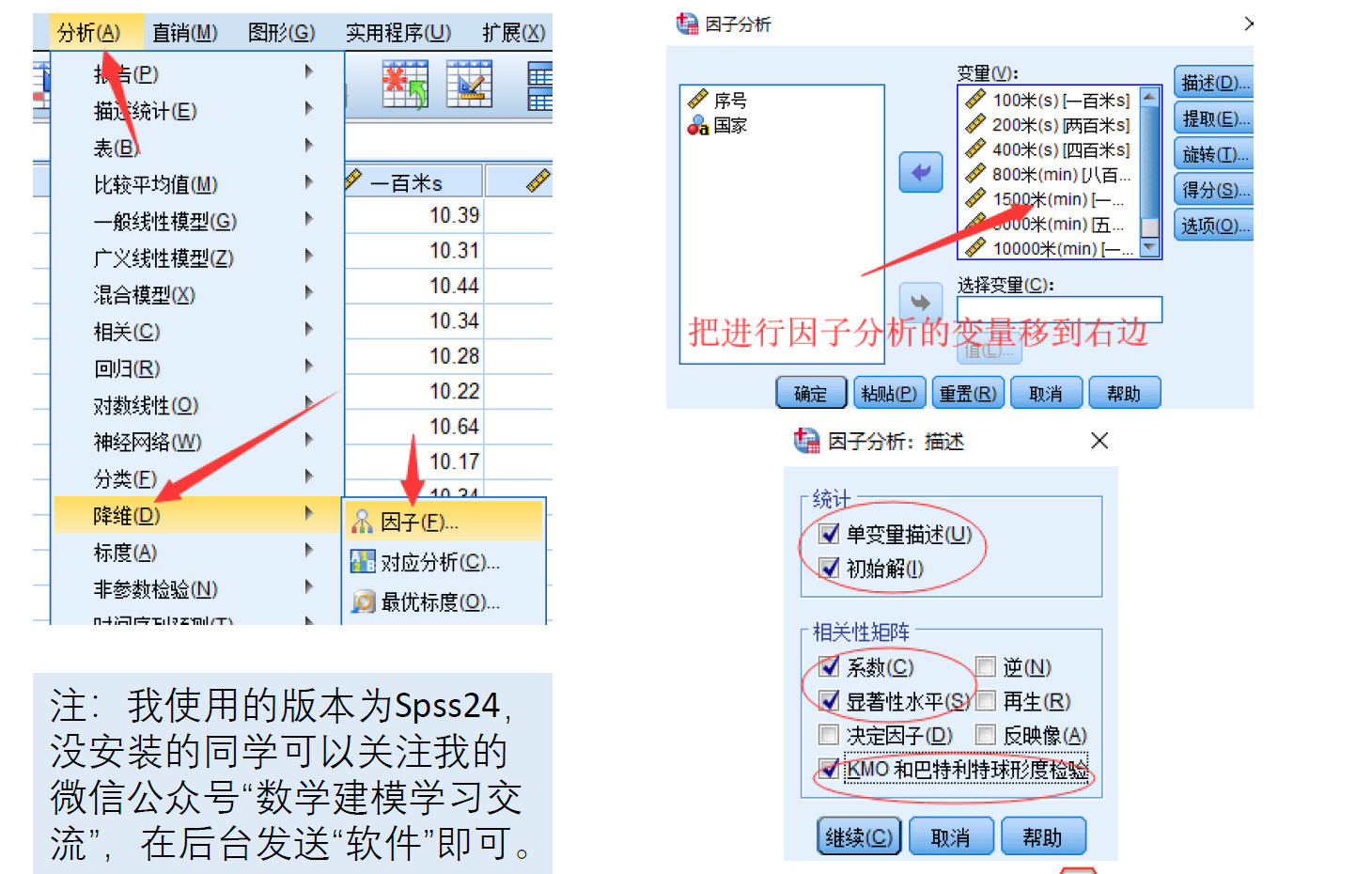
image.png

参数估计

image.png

因子旋转的方法

image.png

因子得分

image.png
注：论文中最常用第三种方法。

因子分析实例（流程）

题目背景

在1984年洛杉矶奥运会田径统计手册中，有55个国家和地区的如下八项男子径赛运动记录：
X1: 100米（单位：秒） x5: 1500米（单位：分）
x2: 200米（单位：秒） x6: 5000米（单位：分）
x3: 400米（单位：秒） x7: 10000米（单位：分）
x4: 800米（单位：秒） x8: 马拉松（单位：分）
请对该数据进行因子分析。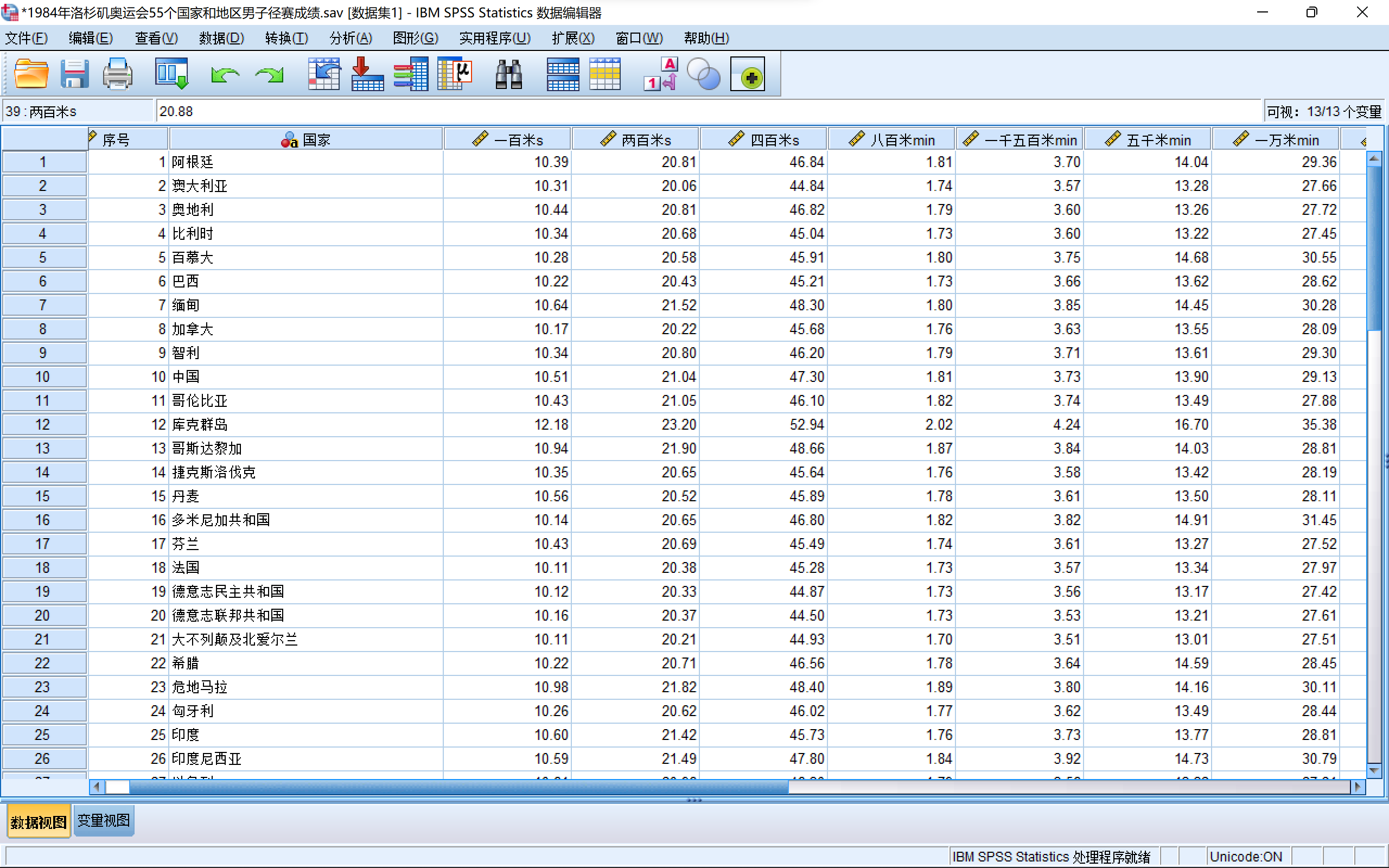
image.png
（SPSS中文版将因子翻译成了组件）

一、第一次运行参数设置

image.png
image.png

二、KMO检验和巴特利特球形检验

（第一次运行因子分析的结果一般作为参考，首先我们要确定原始数据是否适合进行因子分析，即能否通过KMO检验和巴特利特球形检验。）

KMO检验

KMO检验是Kaiser, Meyer和Olkin提出的，该检验是对原始变量之间的简单相关系数和偏相关系数的相对大小进行检验，主要应用于多元统计的因子分析。
KMO统计量是取值在0和1之间，当所有变量间的简单相关系数平方和远远大于偏相关系数平方和时，KMO值越接近于1，意味着变量间的相关性越强，原有变量越适合作因子分析；当所有变量间的简单相关系数平方和接近时，KMO值越接近于0,意味着变量间的相关性越弱，原有变量越不适合作因子分析。
其中，Kaiser给出一个KMO检验标准：KMO>0.9,非常适合；0.8

巴特利特球形检验

巴特利特球形检验是一种检验各个变量之间相关性程度的检验方法。一般在做因子分析之前都要进行巴特利特球形检验，用于判断变量是否适合用于做因子分析。巴特利特球形检验是以变量的相关系数矩阵为出发点的。它的原假设是相关系数矩阵是一个单位阵（不适合做因子分析，指标之间的相关性太差，不适合降维），即相关系数矩阵对角线上的所有元素都是1，所有非对角线上的元素都为0。巴特利特球形检验的统计量是根据相关系数矩阵的行列式得到的。如果该值较大，且其对应的p值小于用户心中的显著性水平（一般为0.05），那么应该拒绝原假设，认为相关系数不可能是单位阵，即原始变量之间存在相关性，适合于作因子分析。相反不适合作因子分析。

实验数据结果图如下：
image.png

  1. KMO值等于0.909，说明数据适合进行因子分析；
  2. 巴特利特球形检验的p值等于0.000，小于0.05，说明我们在95%的置信水平下拒绝原假设，即我们认为数据适合进行因子分析。

    三、调整因子数目再次运行

    碎石检验（scree test）是根据碎石图来决定因素数的方法。Kaiser提出，可通过直接观察特征值的变化来决定因素数。当某个特征值较前一特征值的值出现较大的下降，而这个特征值较小，其后面的特征值变化不大，说明添加相应于该特征值的因素只能增加很少的信息，所以前几个特征值就是应抽取的公共因子数。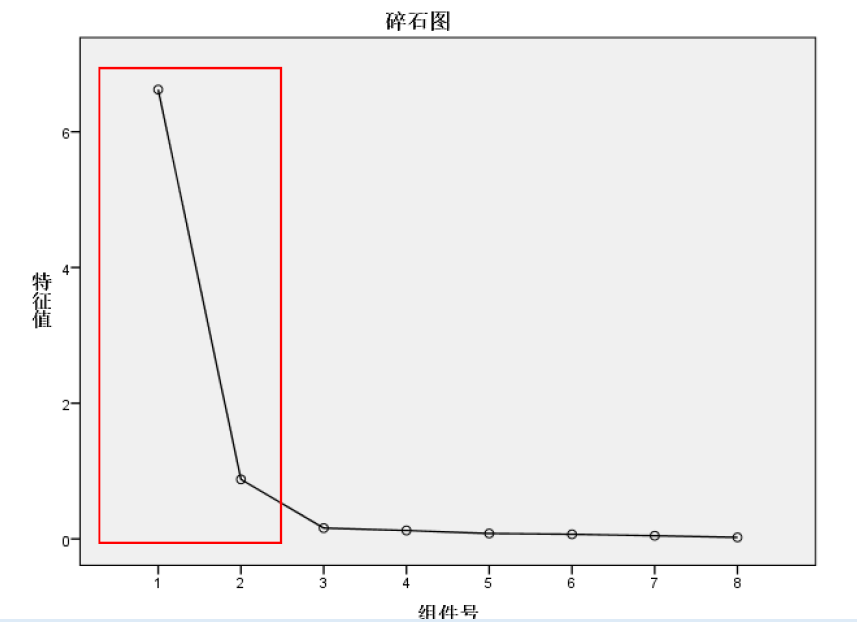
    image.png
    从碎石图可以看出，前两个因子对应的特征值的变化较为陡峭，从第三个因子开始，特征值的变化较为平坦，因此我们应选择两个因子进行分析。
    image.png

    四、解释因子分析结果

    公因子方差表

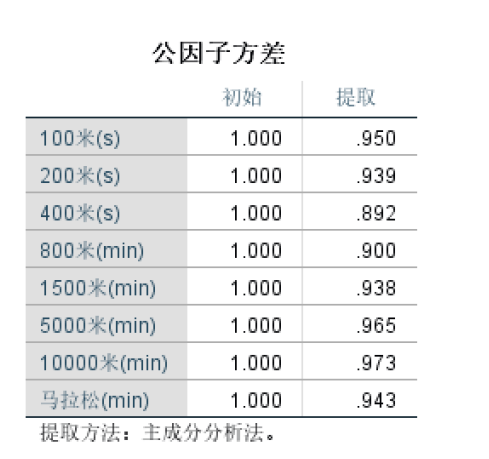
    image.png
    100米(s)这个变量的公因子方差为0.95，这可以解释为我们提取的两个公共因子对100米(s)这个变量的方差贡献率为95%，即这两个公共因子能够反映出（或者说保留）100米(s)这个变量95%的信息。
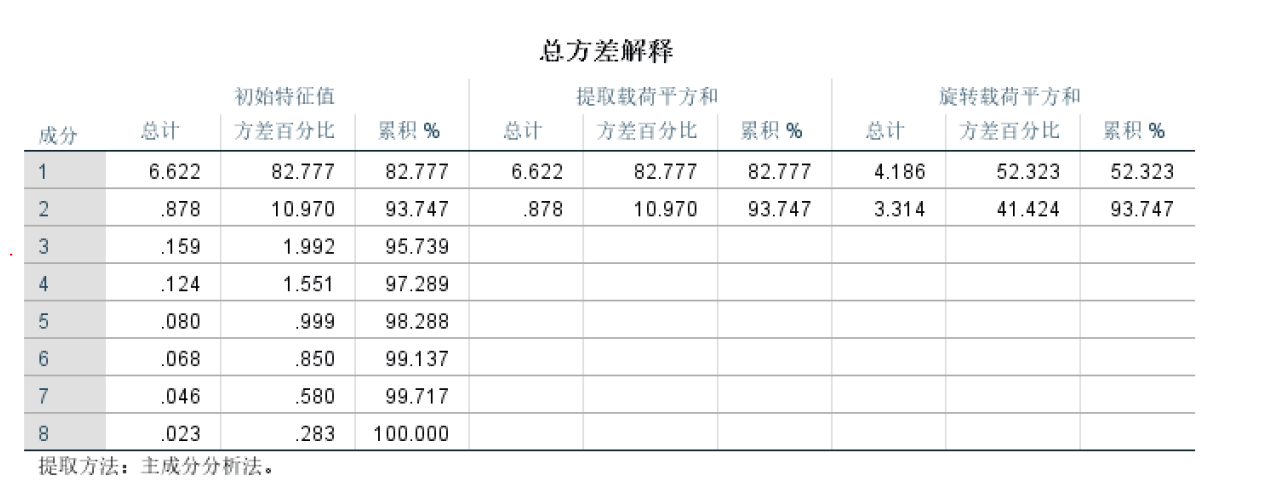
    理论依据：image.png

    总方差解释表

    image.png
    上表为总方差解释表，给出了每个公共因子所解释的方差及累计和。
    从“初始特征值”一栏中可以看出，前2个公共因子解释的累计方差达93.747%，而后面的公共因子的特征值较小，对解释原有变量的贡献越来越小，因此提取两个公共因子是合适的。
    “提取载荷平方和” 一栏是在未旋转时被提取的2个公共因子的方差贡献信息，其与“初始特征值”栏的前两行取值一样。
    “旋转载荷平方和”是旋转后得到的新公共因子的方差贡献信息，和未旋转的贡献信息相比，每个公共因子的方差贡献率有变化，但最终的累计方差贡献率不变。

    成分矩阵

    （解释哪些因子具有相关性）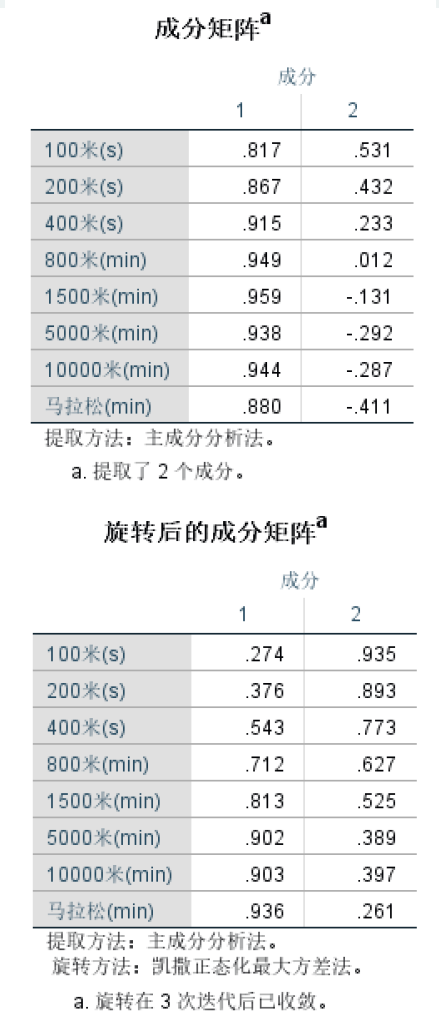
    image.png
    观察两个表格可以发现，旋转后的每个公共因子上的载荷分配更清晰了，因而比未旋转时更容易解释
    各因子的意义。我们在实际应用中只用关注旋转后的因子载荷矩阵即可。
    因子载荷是变量与公共因子的相关系数，当某变量在某公共因子中的载荷绝对值越大，表明该变量与该公共因子更密切，即该公共因子更能代表该变量。由此可知，本例中的第1个公共因子更能代表后面五个变量，我们可以称为长跑因子（或耐力因子）；第2个公共因子更能代表前三个变量，我们可称为短跑因子（爆发力因子）。

    旋转后的因子载荷散点图

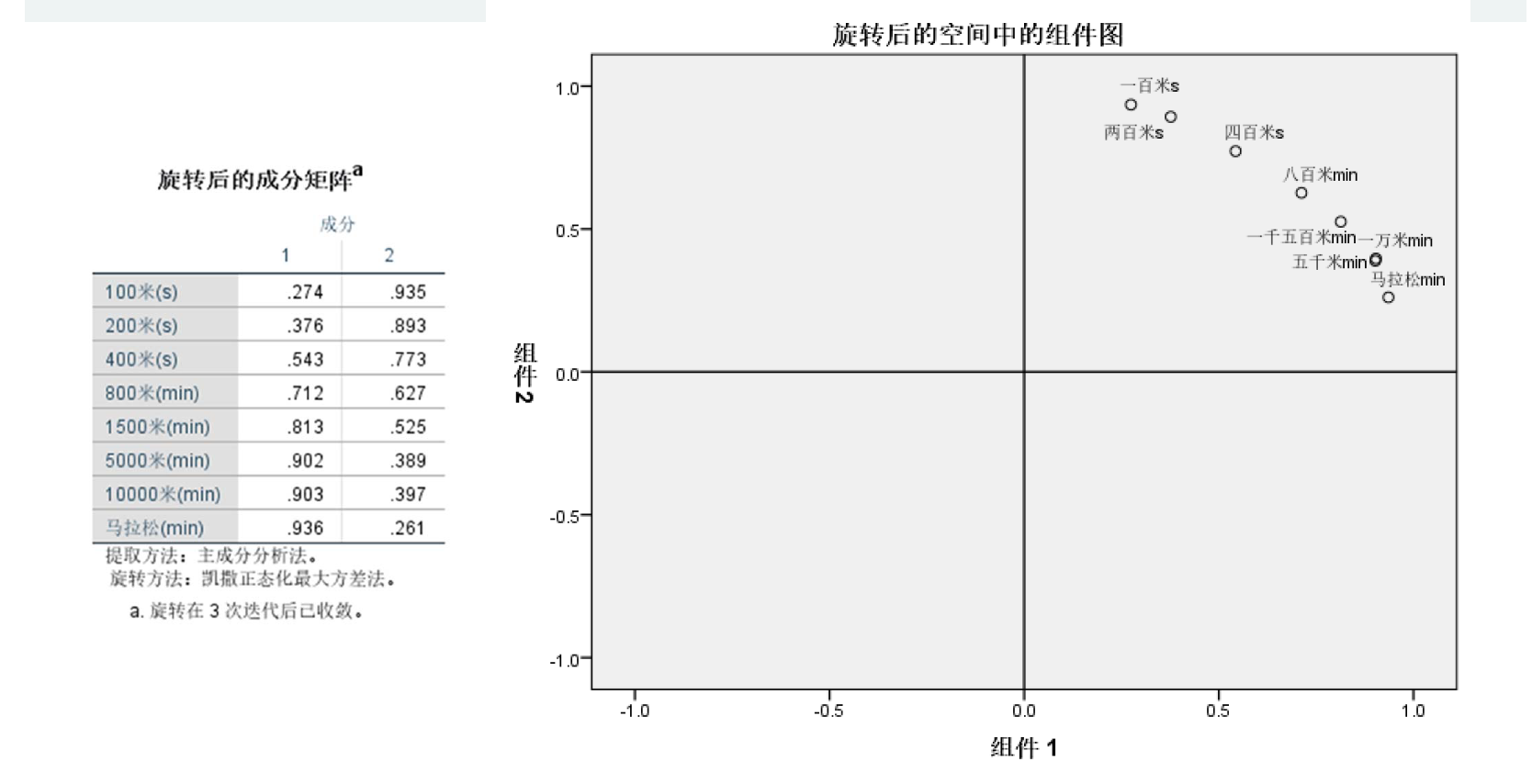
    image.png
    根据“旋转后的成分矩阵”的两列数据所作，由此图观察所得信息与从“旋转成分矩阵”所得信息一致。（如果有三个因子，那么画出来的图就是三维图）

    因子得分

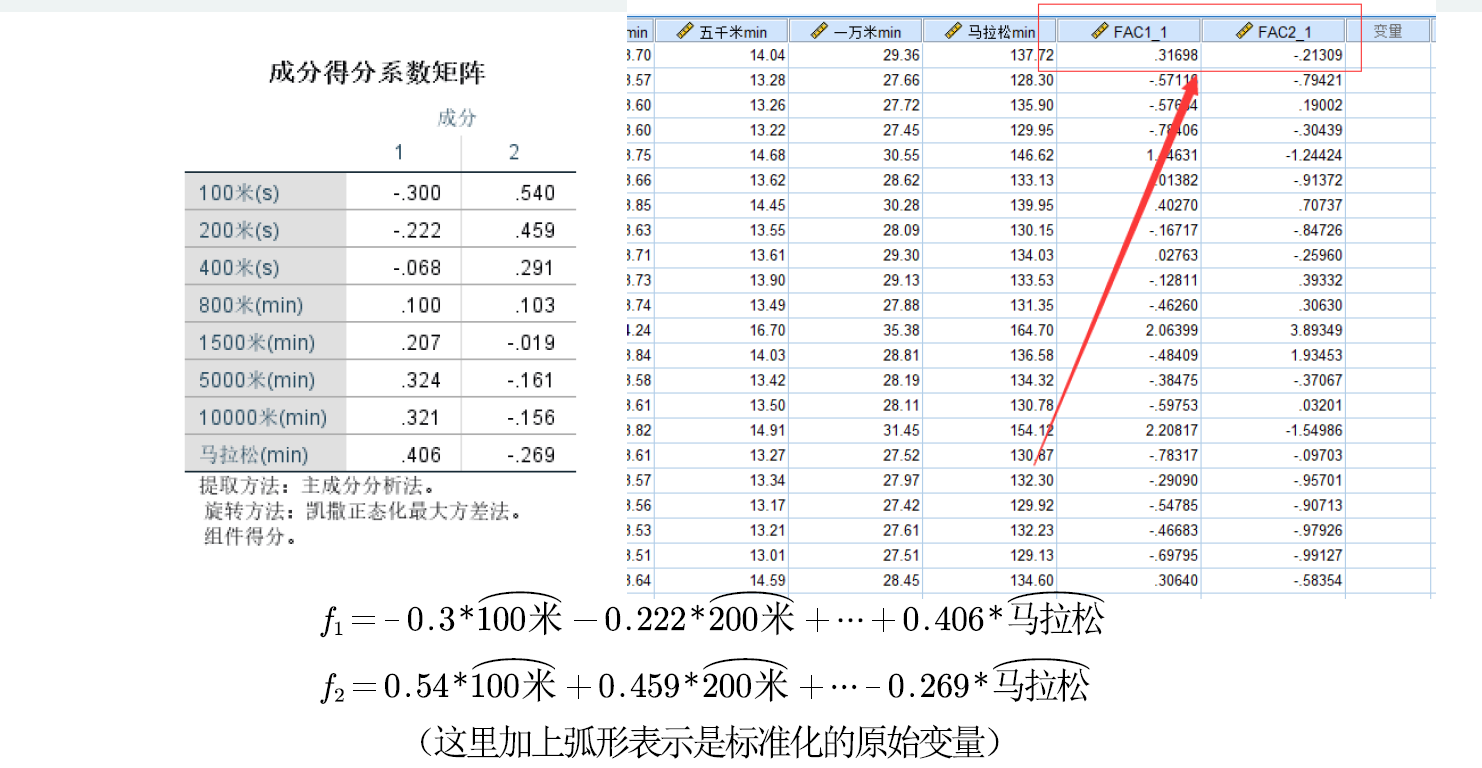
    image.png
    （标准化过程详见主成分分析）
    和主成分分析一样，我们可以用因子得分f1和f2作为两个新的变量，来进行后续的建模（例如聚类、回归等）
    注意：因子分析模型不能用于综合评价，尽管有很多论文是这样写的，但这是存在很大的问题的。例如变量的类型、选择因子的方法、旋转对最终的影响都是很难说清的。

    论文应用：因子分析降维

    image.png因子分析应用：对恐怖袭击事件记录数据的量化分析 .pdf