模板

70%题目是单调性的
25%是一段满足，一段不满足，存在一个两段性的性质
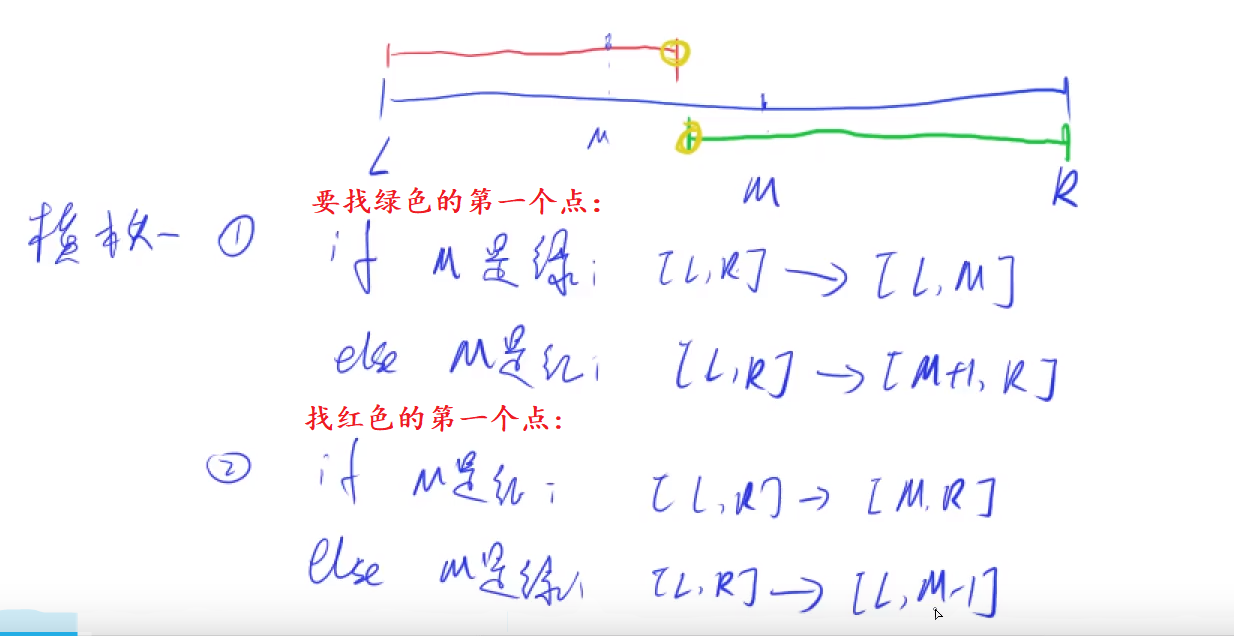
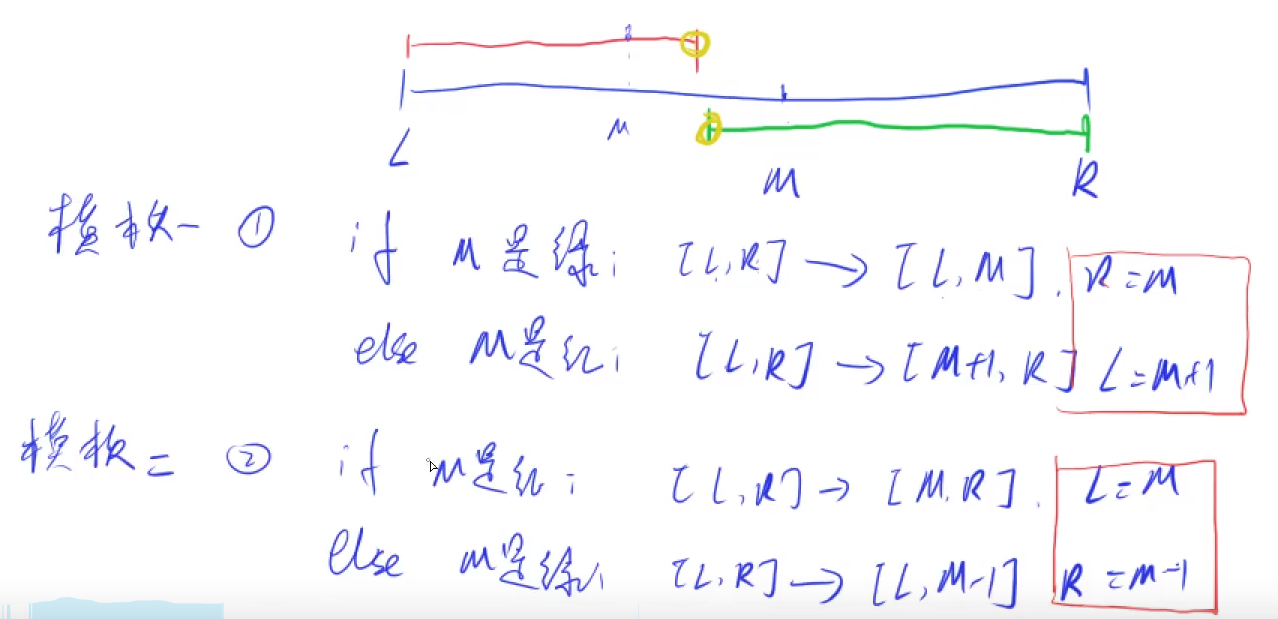
image.png
image.png
image.png

  • 当我们将区间[l, r]划分成[l, mid]和[mid + 1, r]时，其更新操作是r = mid或者l = mid + 1;，计算mid时不需要加1。

    1. int bsearch_1(int l, int r)
    2. {
    3.   while (l < r)
    4.   {
    5.       int mid = l + r >> 1;
    6.       if (check(mid)) r = mid;
    7.       else l = mid + 1;
    8.   }
    9.   return l;//此时l=r;
    10. }

  • 当我们将区间[l, r]划分成[l, mid - 1]和[mid, r]时，其更新操作是r = mid - 1或者l = mid;，此时为了防止死循环，计算mid时需要加1。

    • 例如 r=l+1,则mid=l,whlie之后l=mid陷入死循环
      1. int bsearch_2(int l, int r)
      2. {
      3. while (l < r)
      4. {
      5.    int mid = l + r + 1 >> 1;
      6.    if (check(mid)) l = mid;
      7.    else r = mid - 1;
      8. }
      9. return l;  //此时l=r;
      10. }
      如果写完之后发现是**l = mid**，那么在计算**mid**时需要加上**1**，否则如果写完之后发现是**r = mid**，那么在计算**mid**时不能加**1**。
      **
      二分的流程：
  1. 确定二分边界
  2. 编写二分代码框架
  3. 设计一个check（）
  4. 判断一下区间如何更新
  5. 如果更新方式
    1. l = mid,r = mid-1

      二分查找

      1. class Solution {
      2. public int search(int[] nums, int target) {
      3.   int left = 0;
      4.   int right = nums.length-1;
      5.   int mid = 0;
      6.   while(left<=right) {
      7.       mid = (left+right)>>1;
      8.       if(target < nums[mid]) {
      9.           right = mid-1;
      10.       }else if(target > nums[mid]) {
      11.           left = mid+1;
      12.       }else {
      13.           return mid;
      14.       }
      15.   }
      16.   return -1;
      17. }
      18. }

      以二分查找为模板的题目

      35. 搜索插入位置

      给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

你可以假设数组中无重复元素。

示例 1:

输入: [1,3,5,6], 5
输出: 2
示例 2:

输入: [1,3,5,6], 2
输出: 1
示例 3:

输入: [1,3,5,6], 7
输出: 4
示例 4:

输入: [1,3,5,6], 0
输出: 0

  1. class Solution {
  2.     public int searchInsert(int[] nums, int target) {
  3.         // 第一个>=target的位置
  4.         if(nums.length==0)
  5.             return 0;
  7.         int left = 0,right = nums.length;
  8.         int mid = 0;
  9.         while(left < right) {
  10.             mid = left+right>>1;
  11.             if(nums[mid] >= target) {
  12.                 right = mid;
  13.             } else {
  14.                 left = mid+1;
  15.             }
  16.         }
  17.         return left;
  18.     }
  19. }

153. 寻找旋转排序数组中的最小值

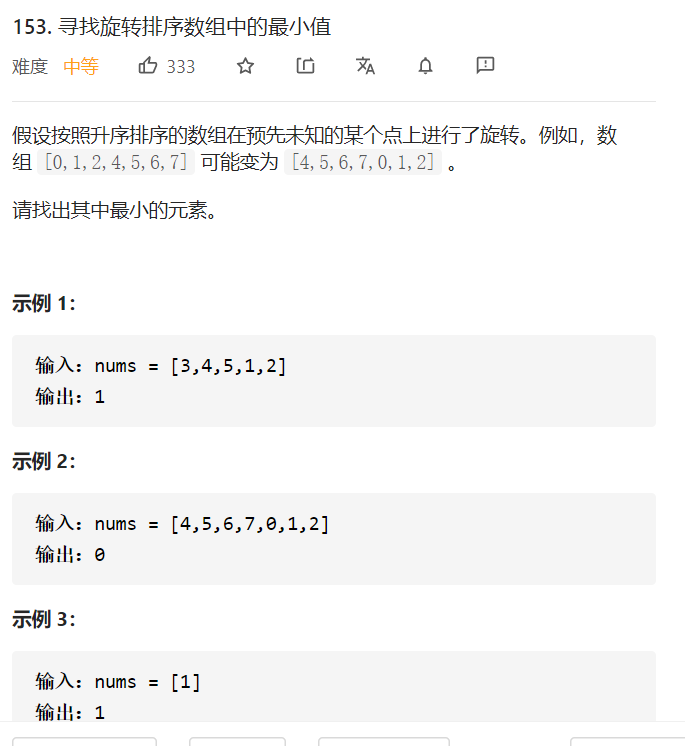
image.png

  1. class Solution {
  2.     public int findMin(int[] nums) {
  3.         int l = 0 , r = nums.length-1;
  4.         int length = nums.length-1;
  5.         while(l < r) {
  6.             int mid= l+r>>1;
  7.             if(nums[mid] > nums[length]) {
  8.                 l =  mid+1;
  9.             } else {
  10.                 r = mid;
  11.             }
  12.         }
  13.         return nums[l];
  14.     }
  15. }

287. 寻找重复数

这个是无法套用模板的题目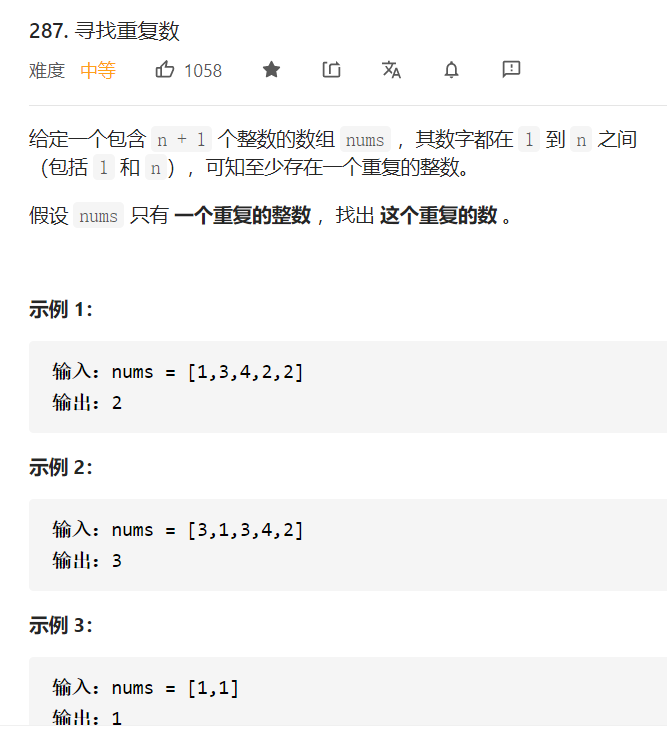
image.png
使用抽屉原理, n*logn

  1. class Solution {
  2.     public int findDuplicate(int[] nums) {
  3.         int left = 1;
  4.         int right = nums.length-1;
  6.         while(left<right) {
  7.             int mid = left+right>>1;
  8.             int cnt = 0;
  9.             for(int x:nums){
  10.                 if(x>=left && x<=mid) {
  11.                     cnt++;
  12.                 }
  13.             }
  14.             if(cnt>mid-left+1) {
  15.                 right = mid;
  16.             } else {
  17.                 left = mid+1;
  18.             }
  19.         }
  20.         return left;
  21.     }
  22. }

没有模板时候自己做的题目

1. 旋转数组的最小数字

做了很久,很恶心
**
https://leetcode-cn.com/problems/xuan-zhuan-shu-zu-de-zui-xiao-shu-zi-lcof/

image.png

  1. class Solution {
  2.     public int minArray(int[] numbers) {
  4.         int left = 0,right=numbers.length-1;
  5.         int mid= 0;
  6.         while(left<=right) {
  7.             mid = (left+right)>>1;
  8.             if(numbers[mid] < numbers[right]) {
  9.                 right = mid;
  10.             } else if (numbers[mid] > numbers[right]) {
  11.                 left = mid+1;
  12.             } else {
  13.                 right-=1;
  14.             }
  15.         }
  16.         return numbers[left];
  17.     }
  18. }

34. 在排序数组中查找元素的第一个和最后一个位置

这个题目的**binarySearch需要仔细看一下,一个函数实现两个功能,可以分别查找target与target+1的元素的起始位置**

给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

进阶：

你可以设计并实现时间复杂度为 O(log n) 的算法解决此问题吗？

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/find-first-and-last-position-of-element-in-sorted-array
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
image.png

  1. class Solution {
  2.     public int[] searchRange(int[] nums, int target) {
  3.         int leftIdx = binarySearch(nums, target, true);
  4.         int rightIdx = binarySearch(nums, target, false) - 1;
  5.         if (leftIdx <= rightIdx && rightIdx < nums.length && nums[leftIdx] == target && nums[rightIdx] == target) {
  6.             return new int[]{leftIdx, rightIdx};
  7.         } 
  8.         return new int[]{-1, -1};
  9.     }
  11.     public int binarySearch(int[] nums, int target, boolean lower) {
  12.         int left = 0, right = nums.length - 1, ans = nums.length;
  13.         while (left <= right) {
  14.             int mid = (left + right) / 2;
  15.             if (nums[mid] > target || (lower && nums[mid] >= target)) {
  16.                 right = mid - 1;
  17.                 ans = mid;
  18.             } else {
  19.                 left = mid + 1;
  20.             }
  21.         }
  22.         return ans;
  23.     }
  24. }
  26. 作者：LeetCode-Solution
  27. 链接：https://leetcode-cn.com/problems/find-first-and-last-position-of-element-in-sorted-array/solution/zai-pai-xu-shu-zu-zhong-cha-zhao-yuan-su-de-di-3-4/
  28. 来源：力扣（LeetCode）
  29. 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

4. 寻找两个正序数组的中位数.

寻找第k大的数字,每次比较num1[(k/2)-1] 和 num2[(k/2)-1];

  • 两者中的小值,因为二者前面都有(k/2)-1个,所以较小值前面最多有k-2个数字,所以他不可能是第k大的数字
  • 所以较小值和它前面的所有值都可以舍去

image.png

  1. class Solution {
  2.     public double findMedianSortedArrays(int[] nums1, int[] nums2) {
  3.         if (nums1.length > nums2.length) {
  4.             return findMedianSortedArrays(nums2, nums1);
  5.         }
  7.         int m = nums1.length;
  8.         int n = nums2.length;
  9.         int left = 0, right = m;
  10.         // median1：前一部分的最大值
  11.         // median2：后一部分的最小值
  12.         int median1 = 0, median2 = 0;
  14.         while (left <= right) {
  15.             // 前一部分包含 nums1[0 .. i-1] 和 nums2[0 .. j-1]
  16.             // 后一部分包含 nums1[i .. m-1] 和 nums2[j .. n-1]
  17.             int i = (left + right) / 2;
  18.             int j = (m + n + 1) / 2 - i;
  20.             // nums_im1, nums_i, nums_jm1, nums_j 分别表示 nums1[i-1], nums1[i], nums2[j-1], nums2[j]
  21.             int nums_im1 = (i == 0 ? Integer.MIN_VALUE : nums1[i - 1]);
  22.             int nums_i = (i == m ? Integer.MAX_VALUE : nums1[i]);
  23.             int nums_jm1 = (j == 0 ? Integer.MIN_VALUE : nums2[j - 1]);
  24.             int nums_j = (j == n ? Integer.MAX_VALUE : nums2[j]);
  26.             if (nums_im1 <= nums_j) {
  27.                 median1 = Math.max(nums_im1, nums_jm1);
  28.                 median2 = Math.min(nums_i, nums_j);
  29.                 left = i + 1;
  30.             } else {
  31.                 right = i - 1;
  32.             }
  33.         }
  35.         return (m + n) % 2 == 0 ? (median1 + median2) / 2.0 : median1;
  36.     }
  37. }