小端模式:末位数在小地址上
大端模式:末位数在大地址上(符合人的习惯)
对于 OX 01234567:
| 地址1 | 地址2 | 地址3 | 地址4 | |
|---|---|---|---|---|
| OX 01234567 大端 | 01 | 23 | 45 | 67 |
| OX 01234567 小端 | 67 | 45 | 23 | 01 |
二进制代码不兼容,很少有二进制代码能在不同机器和操作系统组合之间移植。
移位
左移: 后面补0
右移:
- 逻辑右移:前面补0
- 逻辑右移:前面补符号位
编码
B2U:Binary to Unsigned 二进制到无符号数
B2T:Binary to Two’s Complement 二进制到补码
有符号数
无符号数
有符号数与无符号数的装换
有符号数+无符号数 = 无符号数
有符号数与无符号数的比较也是转换成无符号数进行比较
运算
无符号运算
x
无符号加法
两个无符号数a,b相加,结果=(a+b)%最大值
无符号数的溢出:对于无符号数 a,b 来说,如果s=a+b,并且s<a 或者 s<b,那么就发生了溢出。
无符号乘法
C语言,将一个无符号乘法截断为w位 等价于 计算该值%(2^w)x*y = (x*y)mod (2^w)
补码
加法
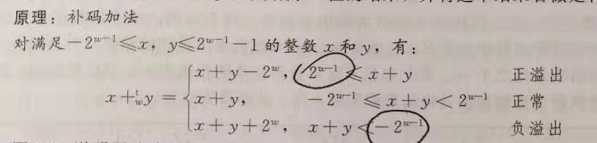
正溢出:x>0,y>0;s= x+y 并且s<=0,正溢出
负溢出:x<0,y<0;s= x+y 并且s>=0,负溢出
补码非
- 方法1:对每一位求反,再+1
- 方法2:找到最后一个1,然后将其前面的所有元素取反
补码最小值的非依然是其自身
除此以外,x取非都是-x
补码乘法
补码乘法相当于先计算该值膜2^w,再把无符号数转为补码
xy = U2T( (xy)mod 2^w )
乘以常数的优化
x14,14=(2+2+2) 则编译器将x14重写为 (x<<3)+(x<<2)+(x<<1)
另外,14=(2-2),则编译器将x*14重写为 (x<<4) - (x<<1)
具体使用哪个,编译器会进行选择。
补码除以2的幂
无符号数x :对于0<=k
有符号数x为负数时候:(x+(1<
对于C语言,算数右移的机器,补码表示:( x<0 ? x+(1<<k)-1:x) >> k
小数
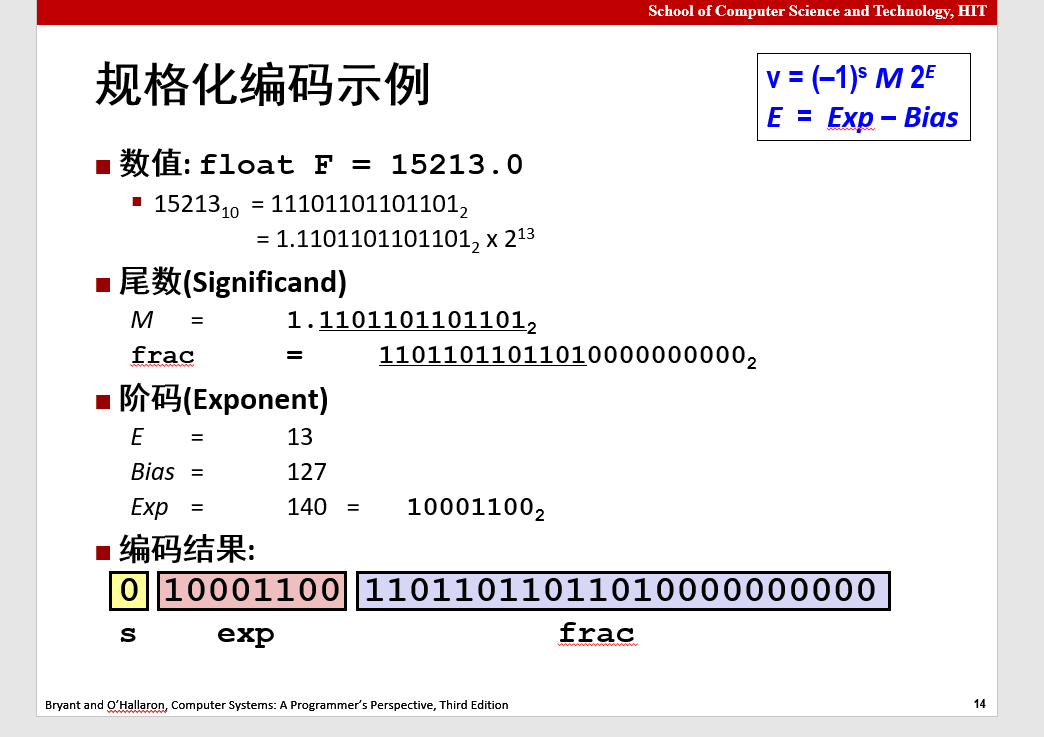
规格化
规格化的exp取值为[1,254],Bias是一个2-1 ,阶码的值=exp-Bias
IEEE
`V=(-1)`* M * 2
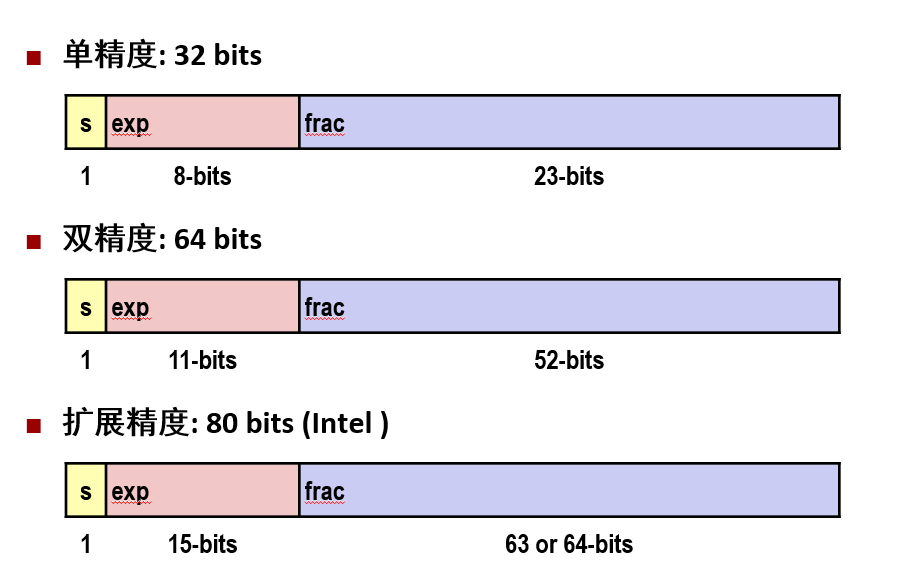
规格化的:exp不能全1,不能全0
- 解嘛用偏置值表示的有符号整数,E=e-Bias,Bias=2-1 则[-126,127]
- 小数字段frac是0<=frac<1,尾数定义为M=1+f,这种定义是获得一个额外精度位的技巧
非规格化的:exp=0
- 阶码值=1-Bias,尾数值M=frac
- 使用1-Bias,是为了从非规格化平滑转换成规格化值的方法
- 意义
- 提供了一种数值0的方法,因为规格化M>=1,因此不能表示0
- 可以表示那些非常接近0的数
无穷大,无穷小:阶码全1,小数全0;根据s判断是正无穷还是负无穷
NaN:阶码全1,小数不为0