1. 两数之和

难度简单10472
image.png
思路：使用hash记录已经遍历过的值，然后判断 目标值减去当前值 的差在不在map之中

  1. class Solution {
  2.     public int[] twoSum(int[] nums, int target) {
  3.         if(nums.length==0)
  4.             return new int[]{};
  5.         Map<Integer,Integer> map = new HashMap(); // key为num[i],value为i
  6.         for(int i = 0 ; i < nums.length;i++) {
  7.             if(map.containsKey(target-nums[i])) { // 判断在不在map里面
  8.                 return new int[]{i,map.get(target-nums[i])};
  9.             } 
  10.             map.put(nums[i],i);  //放入当前值
  11.         }
  12.         return null;
  13.     }
  14. }

2. 两数相加

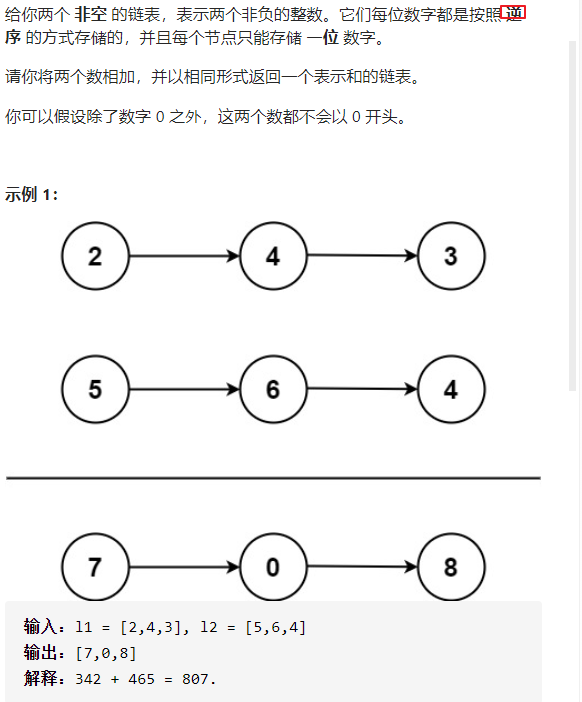
image.png
思路：

  1. 使用一个进位标识来判断是不是产生进位

  2. 遍历完两个数组以后判断一下标志位是不是为1，为1需要+1

    1. class Solution {
    2.  public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
    3.      ListNode dummy = new ListNode(-1);
    4.      ListNode pre = dummy;
    5.      int ten = 0;
    6.      // 两者长度的公共部分
    7.      while(l1!=null && l2!=null) {
    8.          int now = l1.val + l2.val + ten;
    9.          ten = 0;  // 清除之前的进位信息
    10.          if(now>=10)
    11.              ten = 1;
    12.          now = now%10;  // now值为0-9
    13.          pre.next = new ListNode(now);
    14.          pre = pre.next;
    15.          l1 = l1.next;  // 不要忘了往下走
    16.          l2 = l2.next;
    17.      }
    18.      // 其中一个长度比较长，这个时候只需要计算长的和进位标记就行了
    19.      while(l1!=null) {
    20.          int now = l1.val+ten;
    21.          ten = 0;
    22.          if(now>=10)
    23.              ten = 1;
    24.          now = now%10;
    25.          pre.next = new ListNode(now);
    26.          pre = pre.next;
    27.          l1 = l1.next;
    28.      }
    29.      while(l2!=null) {
    30.          int now = l2.val+ten;
    31.          ten = 0;
    32.          if(now>=10)
    33.              ten = 1;
    34.          now = now%10;
    35.          pre.next = new ListNode(now);
    36.          pre = pre.next;
    37.          l2 = l2.next;
    38.      }
    39.      // 两个链表可能会在最后产生进位
    40.      if(ten!=0) {
    41.          pre.next = new ListNode(1);
    42.      }
    43.      return dummy.next;
    44.  }
    45. }

    42. 接雨水

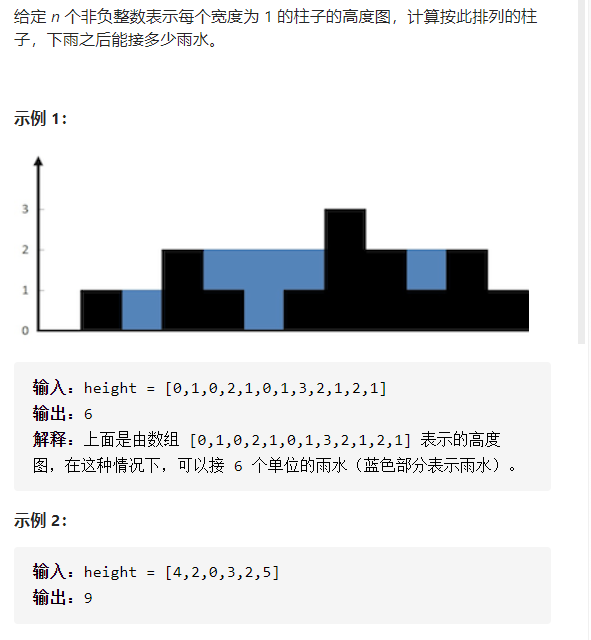
    image.png
    思路：

  3. 定义一个左指针，一个右指针

  4. 如果h[left] < h[right] 则说明左边的比右边的低，那么h[left]一定是被左边走过的最大值leftMax所约束，因为只有左边比右边低的时候，左边才往前走，所以这个时候左边最大值一定是小于等于右边最大值的。

    1. class Solution {
    2.  public int trap(int[] height) {
    3.      int res = 0;
    4.      int left = 0;
    5.      int right = height.length-1;
    6.      int leftMax = 0;
    7.      int rightMax = 0;
    8.      while(left<right) {
    9.          if(height[left] < height[right]) {
    10.              // 这个时候可以确定当前的left指向的位置一定是被leftMax所限定的，
    11.              // 因为现在leftMax一定小于rightMax
    12.              // 如果这个时候leftMax 大于 rightMax ，是不可能的，因为right--只有在右边低的时候才进行，一直前进到rightMax > leftMax
    13.              leftMax = Math.max(leftMax,height[left]);
    14.              res += (leftMax - height[left]);
    15.              left++;
    16.          } else {
    17.              rightMax = Math.max(rightMax,height[right]);
    18.              res += (rightMax - height[right]);
    19.              right--;
    20.          }
    21.      }
    22.      return res;
    23.  }
    24. }

    3. 无重复字符的最长子串

    image.png

    206. 反转链表

    难度简单1561
    image.png

  5. 迭代

    1. class Solution {
    2.  public ListNode reverseList(ListNode head) {
    3.      ListNode dummy = new ListNode(-1);
    4.      ListNode pre = dummy;
    5.      ListNode now = head;
    6.      while(now!=null) {
    7.          ListNode next = now.next;
    8.          now.next = dummy.next;
    9.          dummy.next = now;
    10.          now = next;
    11.      }
    12.      return dummy.next;
    13.  }
    14. }

  6. 递归

    1. 对于A->B->C->D;
    2. 如果CD混产科反转，则A->B->C<-D;
    3. 现在对于B来说，需要让C.next = B；则可以B.next.next = B;B.next = null;现在：
      1. A->B<-C<-D
        1. class Solution {
        2. public ListNode reverseList(ListNode head) {
        3. if(head==null || head.next==null)
        4.    return head;
        5. ListNode newNode = reverseList(head.next);
        6. head.next.next = head;
        7. head.next = null;
        8. return newNode;
        9. }
        10. }

5. 最长回文子串

image.png

  • 遍历每一个位置

    • 把这个位置作为中点找两边

    • 把这个位置作为右边一端的开始

      1. class Solution {
      2. int max = 1;
      3. int left = 0;
      4. public String longestPalindrome(String s) {
      5.    for(int i = 0 ; i < s.length();i++) {
      6.        find(s,i);
      7.    }
      8.    return s.substring(left,max+left);
      9. }
      11. void find(String s,int m) {
      12.    // 作为中点
      13.    for(int l = m-1,r = m+1;l>=0 && r < s.length();l--,r++) {
      14.        if(s.charAt(l)==s.charAt(r)) {
      15.            if(max < r-l+1) {
      16.                max = r-l+1;
      17.                left = l;
      18.            }
      19.        } else {
      20.            break;
      21.        }
      22.    }
      24.    // 作为右边第一个
      25.    for(int l = m-1,r = m;l>=0 && r <s.length();l--,r++) {
      26.        if(s.charAt(l)==s.charAt(r)) {
      27.            if(max < r-l+1) {
      28.                max = r-l+1;
      29.                left = l;
      30.            }
      31.        } else {
      32.            break;
      33.        }
      34.    }
      35. }
      36. }

      11. 盛最多水的容器

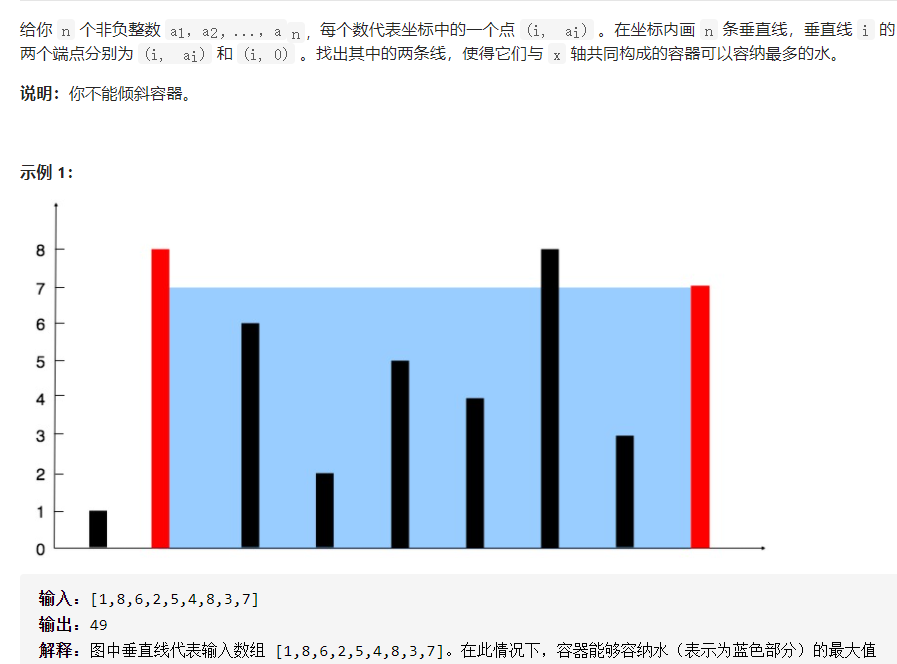
      image.png

  • 使用左右指针

    • res = 长度 * 左右高度的最小值
    • 如果左边低，l++
    • 否则，r++
      • 分析：使其中低的一个边进行移动，那么新边如果比这个边长，则res变大；如果新边比这个短，res会变小；如果移动长的一边，则res一定变小
      • 所以移动段的一边更合适
        1. class Solution {
        2. public int maxArea(int[] height) {
        3. int l = 0,r = height.length-1;
        4. int res = 0;
        5. while(l<r) {
        6.     if(height[l]<height[r]) {
        7.         // 按照短的一边进行计算高度
        8.         res = Math.max(res,(r-l)*height[l]);
        9.         l++; // 移动短的一边的
        10.     }else {
        11.         res = Math.max(res,(r-l)*height[r]);
        12.         r--;
        13.     }
        14. }
        15. return res;
        16. }
        17. }

        53. 最大子序和

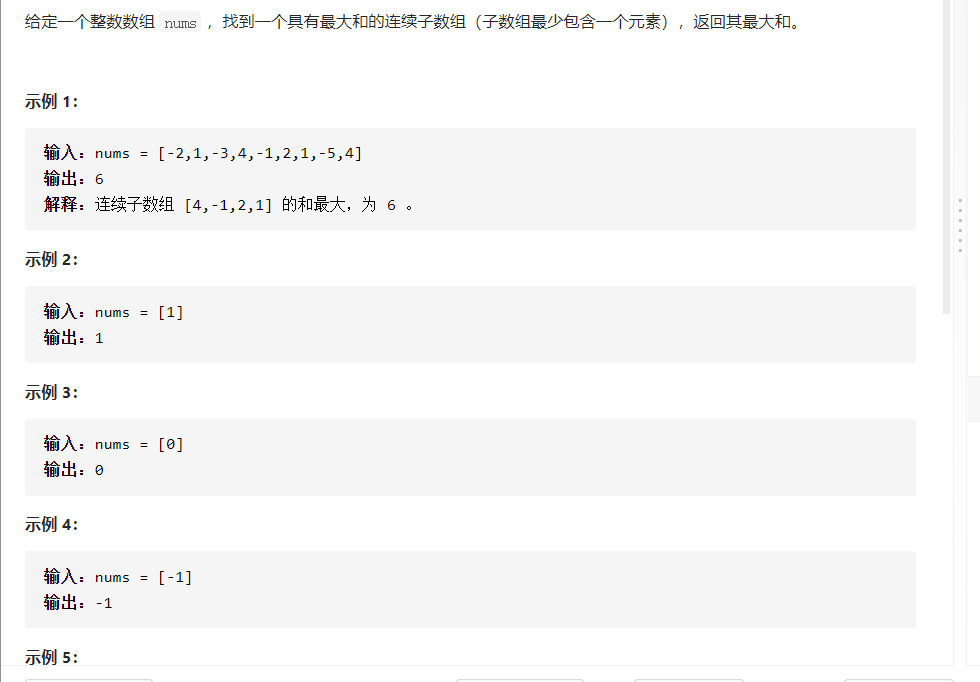
        image.png

  • 使用res记录当前区间的总和，如果res<0，那么丢弃之前的区间；如果res>0,将其放入res的区间中

    1. class Solution {
    2.   public int maxSubArray(int[] nums) {
    3.       if(nums.length==0)
    4.           return 0;
    5.       int res = nums[0];// 默认第一个数是第一个区间
    6.       int max = nums[0];
    7.       for(int i = 1 ; i < nums.length;i++) {
    8.           if(res < 0) { // 之前的区间为负值，没有意义，丢弃
    9.               max = Math.max(nums[i],max);
    10.               res = nums[i];
    11.           } else { // 加上之前区间的值
    12.               max = Math.max(res+nums[i],max);
    13.               res += nums[i];
    14.           }
    15.       }
    16.       return max;
    17.   }
    18. }

    15. 三数之和

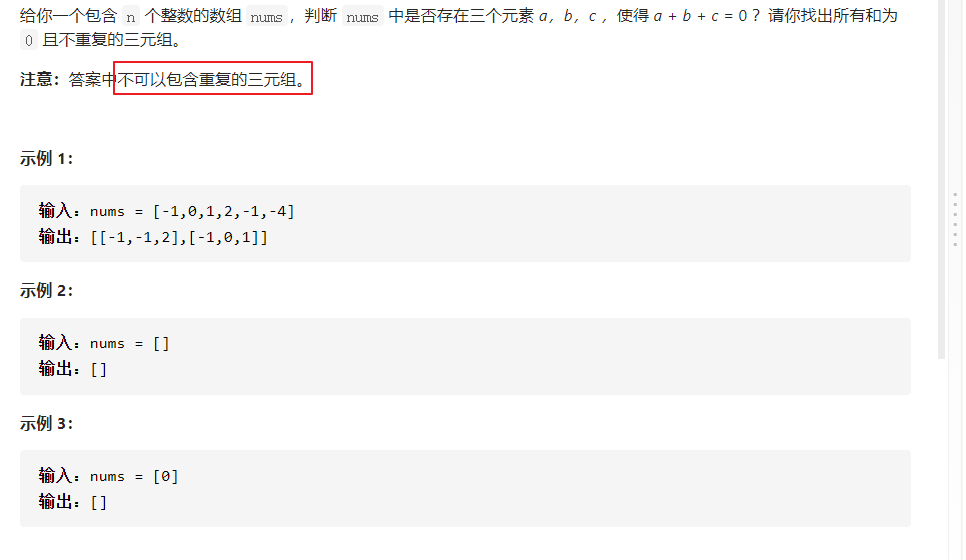
    image.png

  • 排序

  • 按顺序选出第一个元素
    • 第一个元素不能已经出现过
  • 根据第一个元素选出第二个元素
    • 第二个元素在第一个元素已经确定的那么循环中不能已经出现过

  • 根据1,2选第三个数

    1. class Solution {
    2.   public List<List<Integer>> threeSum(int[] nums) {
    3.       List<List<Integer>> res = new ArrayList();
    4.       Arrays.sort(nums);
    5.       for(int i = 0 ; i < nums.length-2;i++) {
    6.           // 开始的头一个元素不能跟之前的元素是一样
    7.           // 例如 [-1,-1,0,1,1]，第二次遍历时候，-1与之前的-1相等，
    8.           // 那么之前的在第二个-1之后如果有两个数使满足条件，
    9.           // 那么在第一个-1的时候，这两个数一定已经被发现了
    10.           if(i!=0 && nums[i]==nums[i-1])
    11.               continue;
    13.           int r = nums.length-1;
    14.           for(int l = i+1;l < nums.length-1;l++) {
    15.               // 对于三个数来说，这个时候第一个数已经确定了，如果第二个数之前已经被添加到了结果集合中
    16.               // 那么第二个数会重复，因为三个数已经确定了第一个数和第二个数，那么第三个数一定也是确定的值
    17.               // 所以第二个数在第一个数确定的时候不能重复
    18.               if(l!=i+1 && nums[l]==nums[l-1]) {
    19.                   continue;
    20.               }
    21.               while(l<r && nums[i]+nums[l]+nums[r]>0) {
    22.                   r--;
    23.               }
    24.               // 后面两个数不能是同一个数
    25.               if(l==r) {
    26.                   break;
    27.               }
    28.               if(l < r && nums[i]+nums[l]+nums[r]==0){
    29.                   List<Integer> list = new ArrayList();
    30.                   list.add(nums[i]);
    31.                   list.add(nums[l]);
    32.                   list.add(nums[r]);
    33.                   res.add(list);
    34.               }
    35.           }
    36.       }
    37.       return res;
    38.   }
    39. }

    33. 搜索旋转排序数组

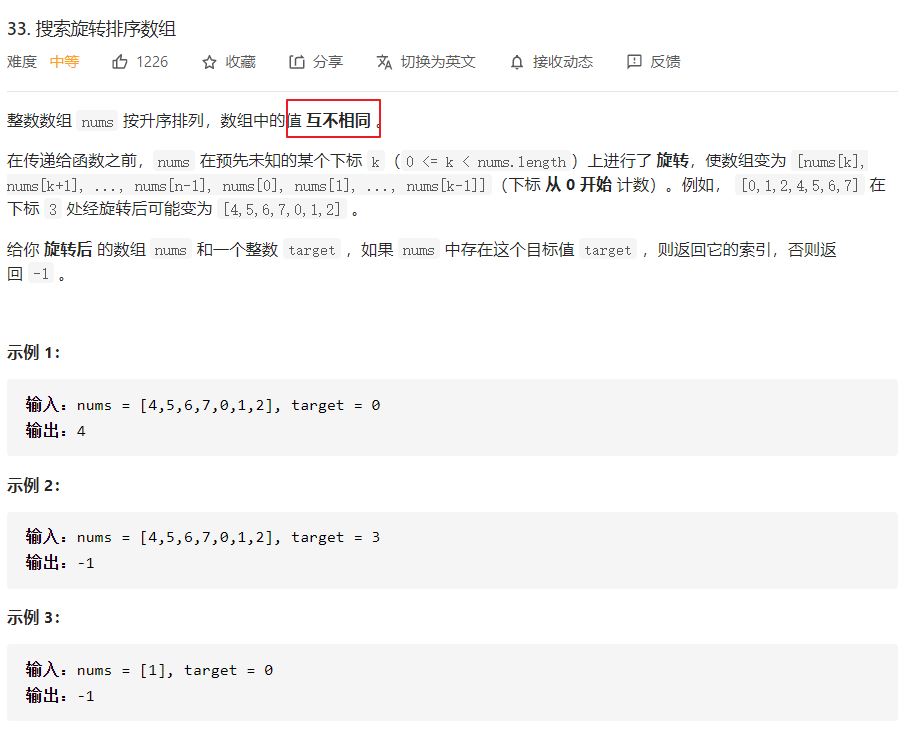
    image.png

  • 二分查找旋转点

  • 二分查找目标值

    1. class Solution {
    2.   public int search(int[] nums, int target) {
    3.       int len = nums.length;
    4.       if(len==0)
    5.           return -1;
    6.       int point = findReversePoint(nums);
    7.       if(point==0){
    8.           return find(nums,0,len-1,target);
    9.       } else {
    10.           // 跟最右边的数比较，如果小于等于就查找右半边
    11.           if(nums[len-1]>=target) {
    12.               return find(nums,point,len-1,target);
    13.           } else { // 查找左半边
    14.               return find(nums,0,point-1,target);
    15.           }
    16.       }
    17.   }
    19.   // 找到旋转点
    20.   int findReversePoint(int[] nums) {
    21.       int l = 0;
    22.       int r = nums.length-1;
    23.       while(l<r) {
    24.           int m = (l+r)>>1;
    25.           // 中点跟左右两边进行对比
    26.           if(nums[m] > nums[r]) {
    27.               l = m+1;
    28.           } else {
    29.               r = m;
    30.           }
    31.       }
    32.       return l;
    33.   }
    35.   // 二分查找
    36.   int find(int[] nums,int l,int r,int target) {
    37.       while(l<r) {
    38.           int m = l+r>>1;
    39.           if(nums[m]<target) {
    40.               l = m+1;
    41.           } else {
    42.               r = m;
    43.           }
    44.       }
    45.       if(nums[l] == target)
    46.           return l;
    47.       return -1;
    48.   }
    49. }

    46. 全排列

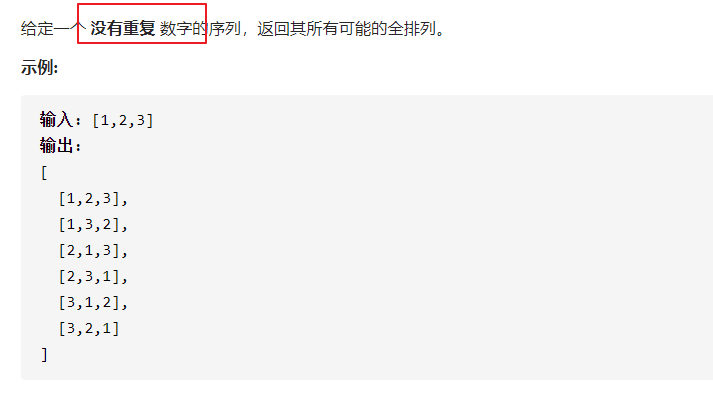
    image.png

  • 使用一个标记数组判断是不是已经访问过

  • 终止条件：已经收集了长度为数组长度的list内容

    1. class Solution {
    2.   public List<List<Integer>> permute(int[] nums) {
    3.       List<List<Integer>> res = new ArrayList();
    4.       List<Integer> list = new ArrayList();
    5.       int len = nums.length;
    6.       if(len==0)
    7.           return res;
    8.       boolean[] flag = new boolean[nums.length];
    9.       find(res,list,0,nums,flag);
    10.       return res;
    11.   }
    13.   void find(List<List<Integer>> res,List<Integer> list,int len,int[] nums,boolean[] flag) {
    14.       if(len==nums.length){
    15.           res.add(new ArrayList(list));
    16.           return;
    17.       }
    18.       for(int i = 0 ; i < nums.length;i++) {
    19.           if(!flag[i]) {
    20.               flag[i] = !flag[i];
    21.               list.add(nums[i]);
    22.               find(res,list,len+1,nums,flag);
    23.               list.remove(len);
    24.               flag[i] = !flag[i];
    25.           }
    26.       }
    27.   }
    28. }

    47. 全排列 II

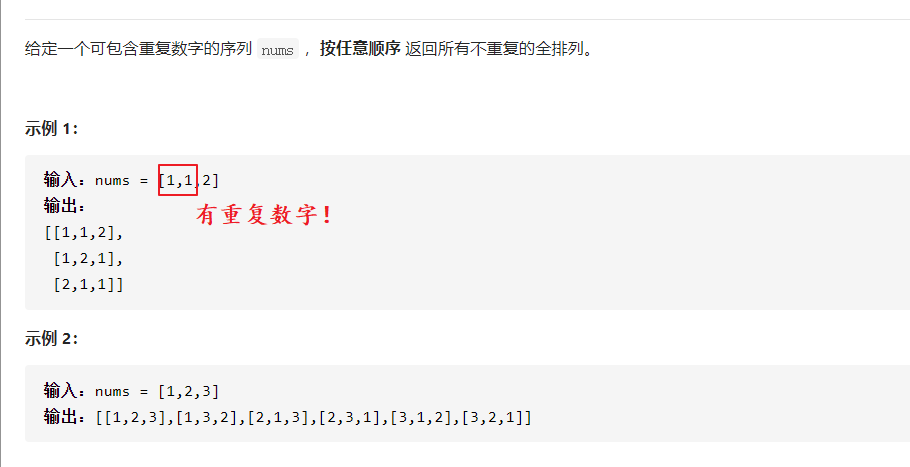
    image.png

    1. class Solution {
    2.   public List<List<Integer>> permuteUnique(int[] nums) {
    3.       int len = nums.length;
    4.       List<List<Integer>> res = new ArrayList();
    5.       List<Integer> list = new ArrayList();
    6.       if(len==0)
    7.           return res;
    8.       Arrays.sort(nums);
    9.       boolean[] flag = new boolean[nums.length];
    10.       find(res,list,0,nums,flag);
    11.       return res;
    12.   }
    14.   void find(List<List<Integer>> res,List<Integer> list,int len,int[] nums,boolean[] flag) {
    15.       if(len==nums.length) {
    16.           res.add(new ArrayList(list));
    17.           return;
    18.       }
    19.       for(int i = 0 ; i < nums.length ; i++) {
    20.           // 如果当前元素之前的元素和自己是一个值，
    21.           // 并且之前的元素还没有加入list，则当前元素不能被加入list
    22.           if(i!=0 && !flag[i-1] && nums[i]==nums[i-1])
    23.               continue;
    25.           if(!flag[i]) {
    26.               flag[i] = !flag[i];
    27.               list.add(nums[i]);
    28.               find(res,list,len+1,nums,flag);
    29.               list.remove(len);
    30.               flag[i] = !flag[i];
    31.           }
    32.       }
    33.   }
    34. }

    21. 合并两个有序链表

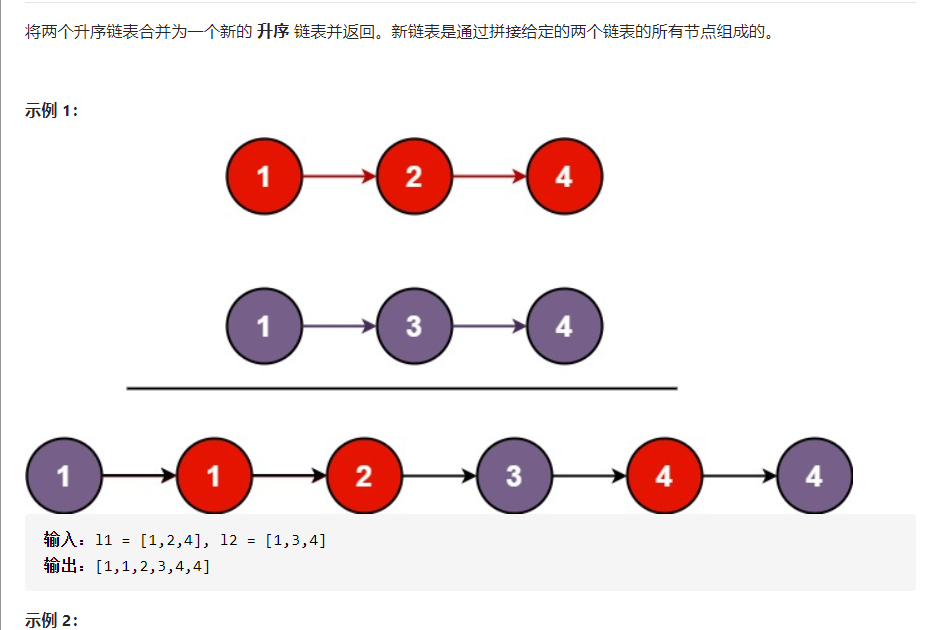
    image.png

    1. class Solution {
    2.   public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
    3.       ListNode dummy = new ListNode(-1);
    4.       ListNode pre = dummy;
    5.       while(l1!=null && l2!=null) {
    6.           if(l1.val < l2.val) {
    7.               pre.next = l1;
    8.               l1=l1.next;
    9.           } else {
    10.               pre.next = l2;
    11.               l2 = l2.next;
    12.           }
    13.           pre =pre.next;
    14.       }
    15.       if(l1!=null) {
    16.           pre.next = l1;
    17.       }
    18.       if(l2!=null) {
    19.           pre.next = l2;
    20.       }
    21.       return dummy.next;
    22.   }
    23. }

    146. LRU 缓存机制

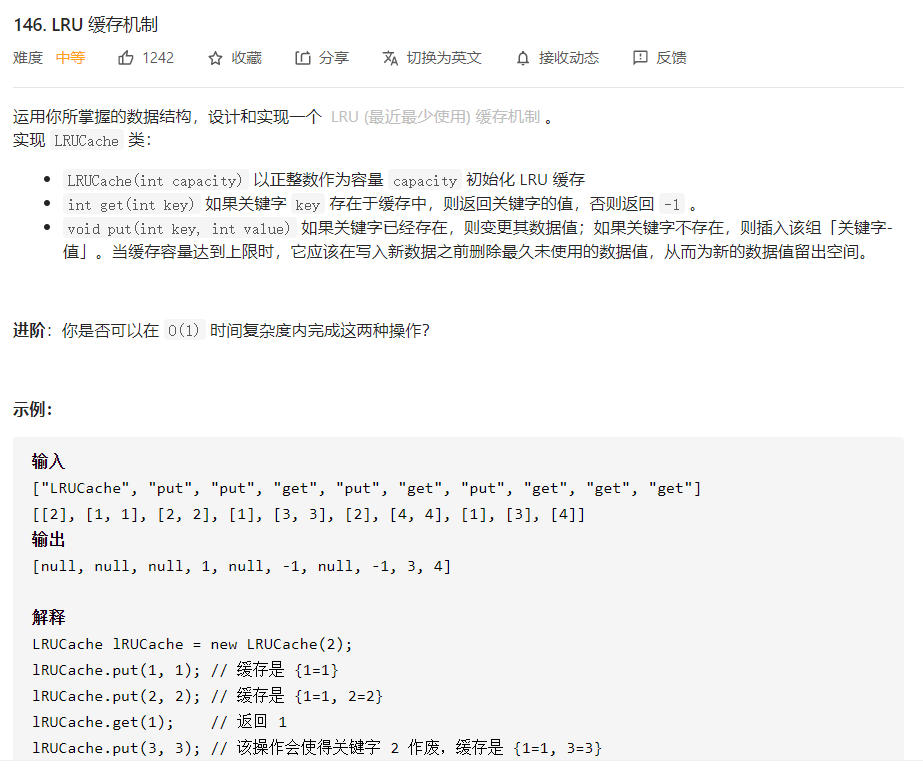
    image.png

  • 创建链表的节点

  • 使用一个map记录已经存在的key
  • 插入到队头

  • 不要忘记更新操作 ```java class LRUCache {

    class Node{

    1.   int key;
    2.   int value;
    3.   Node pre;
    4.   Node next;
    5.   public Node() {}
    6.   public Node(int k,int v) {
    7.       key = k;
    8.       value = v;
    9.   }

    }

  1. Map<Integer,Node> map = new HashMap();
  2. Node head = null;
  3. Node tail = null;
  4. int capacity = 0;
  6. public LRUCache(int capacity) {
  7.     head = new Node();
  8.     tail = new Node();
  9.     head.next = tail;
  10.     tail.pre = head;
  11.     this.capacity = capacity;
  12. }
  14. public int get(int key) {
  15.     if(!map.containsKey(key)) {
  16.         return -1;
  17.     }
  18.     Node now = map.get(key);
  19.     int value = now.value;
  20.     // 将这个Node放到队头
  21.     if(now!=head.next) {
  22.         // 处理now前后节点
  23.         now.pre.next = now.next;
  24.         now.next.pre = now.pre;
  26.         // 处理head的后面节点
  27.         head.next.pre = now;
  28.         now.next = head.next;
  29.         head.next = now;
  30.         now.pre = head;
  31.     }
  32.     return value;
  33. }
  35. public void put(int key, int value) {
  36.     if(!map.containsKey(key)) {
  37.         Node now = new Node(key,value);
  38.         map.put(key,now); 
  39.         // 直接插入到队头,处理head的后面节点
  40.         head.next.pre = now;
  41.         now.next = head.next;
  42.         head.next = now;
  43.         now.pre = head;
  45.         if(capacity==0) {
  46.             map.remove(tail.pre.key); // 从map删除节点
  47.             // 删除最后一个node
  48.             tail.pre.pre.next = tail;
  49.             tail.pre = tail.pre.pre;
  50.         }else {
  51.             capacity--;
  52.         }
  53.     } else {
  54.         // 已经有这个key了
  55.         Node now = map.get(key);
  56.         now.value = value; // 第一次忘了更新这个出错
  57.         if(now!=head.next) {
  58.             // 处理now前后节点
  59.             now.pre.next = now.next;
  60.             now.next.pre = now.pre;
  62.             // 处理head的后面节点
  63.             head.next.pre = now;
  64.             now.next = head.next;
  65.             head.next = now;
  66.             now.pre = head;
  67.         }
  68.     }
  69. }

}

  1. <a name="ka5aW"></a>
  2. #### [31. 下一个排列](https://leetcode-cn.com/problems/next-permutation/)
  3. ![image.png](https://cdn.nlark.com/yuque/0/2021/png/8429887/1615870629659-fdcfbc65-6671-45b3-ab6b-5e488ad47236.png#align=left&display=inline&height=768&margin=%5Bobject%20Object%5D&name=image.png&originHeight=768&originWidth=677&size=43478&status=done&style=none&width=677)
  5. - 我们需要将一个左边的「较小数」与一个右边的「较大数」交换，以能够让当前排列变大，从而得到下一个排列。
  6. - 同时我们要让这个「较小数」尽量靠右，而「较大数」尽可能小。当交换完成后，「较大数」右边的数需要按照升序重新排列。这样可以在保证新排列大于原来排列的情况下，使变大的幅度尽可能小。
  7. 1. 首先从后向前查找第一个顺序对 (i,i+1)(i,i+1)，满足 a[i] < a[i+1]a[i]<a[i+1]。这样「较小数」即为 a[i]a[i]。此时 [i+1,n)[i+1,n) 必然是下降序列。
  8. 1. 如果找到了顺序对，那么在区间 [i+1,n)[i+1,n) 中从后向前查找第一个元素 jj 满足 a[i] < a[j]a[i]<a[j]。这样「较大数」即为 a[j]a[j]。
  9. 1. 交换 a[i]a[i] 与 a[j]a[j]，此时可以证明区间 [i+1,n)[i+1,n) 必为降序。我们可以直接使用双指针反转区间 [i+1,n)[i+1,n) 使其变为升序，而无需对该区间进行排序。
  10. ```java
  11. class Solution {
  12.     public void nextPermutation(int[] nums) {
  13.         if(nums.length<=1)
  14.             return;
  15.         int reverseL = nums.length-2; // 被反转区间的左边界
  16.         int reverseR = nums.length-1; // 被反转区间的右边界
  17.         while(reverseL>=0 && nums[reverseL] >= nums[reverseL+1]) {
  18.             reverseL--; // 找到第一个reverseL指向的数小于其后面一个数字的数 [1,3,5,4,2,1] 则找到数字三的位置，因为3<5
  19.         }
  20.         // reverseL!=-1则说明存在上面说的这样一个reverseL，否则数组就是全局逆序的
  21.         if(reverseL!=-1) {
  22.             while(reverseR>reverseL && nums[reverseR]<=nums[reverseL]){
  23.                     reverseR--;
  24.             }
  25.             int t = nums[reverseL];
  26.             nums[reverseL] = nums[reverseR];
  27.             nums[reverseR] = t;
  28.         }
  29.         // 反转逆序的数组，[1,3,5,4,2,1]此时变成了[1,4,5,3,2,1]，
  30.         // 5,3,2,1是逆序的，将其变为顺序即可，直接反转就行
  31.         reverseL++;
  32.         reverseR = nums.length-1;
  33.         while(reverseL<reverseR) {
  34.             int t = nums[reverseL];
  35.             nums[reverseL] = nums[reverseR];
  36.             nums[reverseR] = t;
  37.             reverseL++;reverseR--;
  38.         }
  39.     }
  40. }

7. 整数反转

image.png

image.png

  1. class Solution {
  2.     public int reverse(int x) {
  3.         int rev = 0;
  4.         while (x != 0) {
  5.             int pop = x % 10;
  6.             x /= 10;
  7.             if (rev > Integer.MAX_VALUE/10 || (rev == Integer.MAX_VALUE / 10 && pop > 7)) return 0;
  8.             if (rev < Integer.MIN_VALUE/10 || (rev == Integer.MIN_VALUE / 10 && pop < -8)) return 0;
  9.             rev = rev * 10 + pop;
  10.         }
  11.         return rev;
  12.     }
  13. }

215. 数组中的第K个最大元素

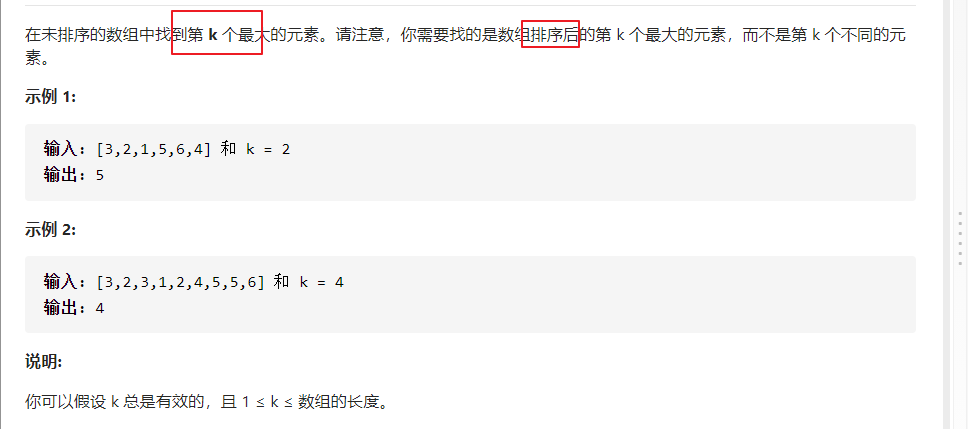
image.png

  • 两种方法
    • 使用优先级队列，进行堆排序 ```java import java.util.*;

public class Solution { public int findKth(int[] a, int n, int K) { // write code here PriorityQueue queue = new PriorityQueue<>(new Comparator(){ public int compare(Integer i1,Integer i2) { return i1-i2; // 一个小顶堆 } }); for(int i = 0 ; i < K ; i ++) { queue.add(a[i]); // 填充这个堆 } for(int i = K;i < n;i++) { if(queue.peek() < a[i]){ queue.poll(); queue.add(a[i]); } } return queue.poll(); } }

  2.    - 使用快速排序
  3. ```java
  4. import java.util.*;
  6. public class Solution {
  7.     public int findKth(int[] a, int n, int K) {
  8.         return find(a,n-K,0,n-1);
  9.     }
  11.     // k 代表的是查找的元素在数组中的位置
  12.     // [l,r]是查找区间
  13.     int find(int[] nums,int k,int l,int r) {
  14.         int temp = nums[l];
  15.         int left = l;
  16.         int right = r;
  17.         while(l<r) {
  18.             while(l<r && nums[r]>=temp) {
  19.                 r--;
  20.             }
  21.             while(l<r && nums[l]<=temp){
  22.                 l++;
  23.             }
  24.             if(l<r) {
  25.                 int t = nums[l];
  26.                 nums[l] = nums[r];
  27.                 nums[r] = t;
  28.             }
  29.         }
  30.         nums[left] = nums[l];
  31.         nums[l] = temp;
  34.         if(l==k) {
  35.             return nums[l];
  36.         }else if(l<k){
  37.             return find(nums,k,l+1,right);  // 查找[l+1,r]
  38.         } else {
  39.             return find(nums,k,0,l-1); // 查找[0,l-1];
  40.         }
  41.     }
  42. }