25. K 个一组翻转链表

image.png

  1. public class Solution {
  2.     public ListNode reverseKGroup (ListNode head, int k) {
  3.         ListNode dummy = new ListNode(-1);
  4.         dummy.next = head; 
  5.         ListNode start = head; //每一段开始的节点
  6.         ListNode pre = dummy; //每一段之前的节点
  7.         while(start!=null) {
  8.             int len = 1;
  9.             ListNode end = start; // end是当前段的最后一个节点
  10.             while(len<k) {
  11.                 len++;
  12.                 if(end.next!=null)
  13.                     end = end.next;
  14.                 else
  15.                     return dummy.next;
  16.             }
  18.             // 现在end 指向当前段的最后一个节点
  20.             ListNode nextStart = null; // 指向下一个区间的最后一个
  21.             if(end!=null)
  22.                 nextStart = end.next;
  24.             reverse(start,end,pre); // 反转[start,end]，并将pre指向新头节点
  26.             while(pre.next!=null) {
  27.                 pre = pre.next;  // pre移到当前段的末尾
  28.             }
  29.             // 连接新段
  30.             pre.next = nextStart;
  31.             start = nextStart; // 重新开始反转
  32.         }
  33.         return dummy.next;
  34.     }
  36.     // 反转[start,end]中间的所有节点，并将其挂在pre的next上
  37.     public void reverse(ListNode start,ListNode end,ListNode pre) {
  38.         end.next = null;
  39.         ListNode now = start.next;
  40.         start.next = null;
  41.         while(now!=null) {
  42.             ListNode nex = now.next;
  43.             now.next = pre.next;
  44.             pre.next = now;
  45.             now = nex;
  46.         }
  47.     }
  48. }

4. 寻找两个正序数组的中位数

image.png
image.png

  1. class Solution {
  2.     public double findMedianSortedArrays(int[] nums1, int[] nums2) {
  3.         int m = nums1.length; // num1的长度
  4.         int n = nums2.length; // num2的长度
  5.         if(m==0) {                  // 如果其中一个没有数据，只需要返回就可以了
  6.             if((n&1)==0) {          // 第二个是偶数时候，需要找到中间的两个取平均
  7.                 return (nums2[n/2]+nums2[n/2-1])/2.0;
  8.             } else {                // 第二个是奇数长度，
  9.                 return nums2[n/2];
  10.             }
  11.         } else if(n==0) {
  12.             if((m&1)==0) {
  13.                 return (nums1[m/2]+nums1[m/2-1])/2.0;
  14.             } else {
  15.                 return nums1[m/2];
  16.             }
  17.         } else if(n==1 && m==1) {
  18.             return (nums1[0]+nums2[0])/2.0;
  19.         }
  21.         // 两个都是有效数组，需要进行判断
  22.         int len = m+n;
  23.         if((len&1)==0) {  // 总长度是偶数，需要取两个值
  24.             int k1 = len/2;
  25.             int k2 = k1+1;
  26.             int a = find(nums1,nums2,k1);
  27.             int b = find(nums1,nums2,k2);
  28.             return (a+b)/2.0;
  29.         } else{          // 总长度是奇数，只需要取一个值就可以了
  30.             int k = len / 2 + 1;
  31.             return find(nums1,nums2,k)/1.0;
  32.         }
  33.     }
  35.     int find(int[] nums1,int[] nums2,int k){
  36.         int l1 = 0; // num1的起始位置
  37.         int l2 = 0;
  38.         int r1 = nums1.length-1; // num1的结束位置
  39.         int r2 = nums2.length-1;
  40.         while(l1<=r1 && l2 <=r2) { 
  41.             int len1 = k/2-1; // num1的有效长度
  42.             int len2 = k/2-1;
  43.             if(l1+len1>r1){  // 如果超出边界，按到最右边的长度进行处理
  44.                 len1 = r1-l1;
  45.             }
  46.             if(l2+len2>r2) {
  47.                 len2 = r2-l2;
  48.             }
  49.             // System.out.println("l1="+l1);
  50.             // System.out.println("len1="+len1);
  51.             // System.out.println("l2="+l2);
  52.             // System.out.println("len2="+len2);
  54.             // 如果num2的位置k比较小，那么更新num2的起始位置
  55.             if(nums1[l1+len1]>nums2[l2+len2]) {
  56.                 k-=(len2+1); // 删除nnum2的以判断的长度
  57.                 l2 = l2+len2+1;
  58.                 if(l2>r2) {  // num2如果已经没有数据了
  59.                     return nums1[l1+k-1]; 
  60.                 }
  61.             } else {
  62.                 k-=(len1+1);
  63.                 l1 = l1+len1+1;
  64.                 if(l1>r1) {
  65.                     return nums2[l2+k-1];
  66.                 }
  67.             }
  68.             if(k==1){  // 如果最后两个数组都是长度大与等于1的
  69.                 return Math.min(nums1[l1],nums2[l2]);
  70.             }
  71.         }
  72.         return -1;
  73.     }
  74. }

56. 合并区间

image.png

  • 开始时间从小到大排序

    1. class Solution {
    2.   public int[][] merge(int[][] intervals) {
    3.       // 进行排序，按照开始时间从大到小并且结束时间同样
    4.       Arrays.sort(intervals,new Comparator<int[]>(){
    5.           public int compare(int[] v1,int[] v2) {
    6.               if(v1[0]==v2[0])
    7.                   return v1[1]-v2[1];
    8.               return v1[0]-v2[0];
    9.           }
    10.       });
    11.       List<int[]> res = new ArrayList();
    12.       int len = intervals.length;
    13.       if(len==0)
    14.           return new int[][]{};
    15.       res.add(intervals[0]);
    16.       int index = 0;
    18.       for(int i = 1 ; i < len;i++) {
    19.           // 如果后面的开始时间小于前面的结束时间，可以合并
    20.           if(intervals[i][0] <= res.get(index)[1]) {
    21.               res.get(index)[1] = Math.max(intervals[i][1],res.get(index)[1]); // 注意[1,4]，[2,3] 时候，前面的可能包含后面的情况，所以更新时候需要判断下
    22.           }else {
    23.               res.add(intervals[i]);
    24.               index++;
    25.           }
    26.       }
    27.       int[][] result = new int[res.size()][2];
    28.       for(int i = 0; i <= index;i++) {
    29.           result[i] = res.get(i);
    30.       }
    31.       return result;
    32.   }
    33. }

    121. 买卖股票的最佳时机

    image.png

    1. class Solution {
    2.   public int maxProfit(int[] prices) {
    3.       int len = prices.length;
    4.       if(len<=1)
    5.           return 0;
    6.       int min = prices[0];
    7.       int max = 0;
    8.       for(int i = 1; i < len;i++) {
    9.           max = Math.max(max,prices[i]-min);
    10.           min = Math.min(min,prices[i]);
    11.       }
    12.       return max;
    13.   }
    14. }

    122. 买卖股票的最佳时机 II

    image.png

    1. class Solution {
    2.   public int maxProfit(int[] prices) {
    3.       int res = 0;
    4.       for(int i = 1 ; i < prices.length;i++) {
    5.           res += (prices[i]>prices[i-1]?prices[i]-prices[i-1]:0);
    6.       }
    7.       return res;
    8.   }
    9. }

    123. 买卖股票的最佳时机 III

    image.png
    image.png

image.pngimage.png

  1. class Solution {
  2.     public int maxProfit(int[] prices) {
  3.         int len = prices.length;
  4.         if(len<=1)
  5.             return 0;
  6.         int buy1 = -prices[0];
  7.         int sell1 = 0;
  8.         int buy2 = -prices[0];
  9.         int sell2 = 0;
  10.         for(int i = 1; i < len; i++) {
  11.             buy1 = Math.max(-prices[i],buy1);
  12.             sell1 = Math.max(buy1 + prices[i],sell1);
  13.             buy2 = Math.max(sell1 - prices[i],buy2);
  14.             sell2 = Math.max(buy2 + prices[i],sell2);
  15.         }
  16.         return Math.max(sell1,sell2);
  17.     }
  18. }

188. 买卖股票的最佳时机 IV

image.png
image.png
image.png
image.png
image.png

  1. class Solution {
  2.     public int maxProfit(int k, int[] prices) {
  3.         int len = prices.length;
  4.         if(len==0 || k==0)
  5.             return 0;
  7.         int[] buy = new int[k];
  8.         int[] sell = new int[k];
  9.         Arrays.fill(buy,-prices[0]); // 第一天无论买多少次,buy都是-pricre[0],sell都是0
  11.         for(int i = 1; i < len ; i++) {
  12.             // 第i天进行第一次买卖
  13.             buy[0] = Math.max(buy[0],-prices[i]);
  14.             sell[0] = Math.max(sell[0],prices[i]+buy[0]); 
  15.             // 第i天进行第j次买卖
  16.             for(int j = 1 ; j < k ; j++) {
  17.                 buy[j] = Math.max(buy[j],sell[j-1]-prices[i]);
  18.                 sell[j] = Math.max(sell[j],prices[i]+buy[j]);
  19.             }
  20.         }
  21.         // System.out.println(Arrays.toString(sell));
  22.         return sell[k-1];
  23.     }
  24. }

注意：
sell[i][j] = Math.max(sell[i-1][j],buy[i-1][j-1]+prices[i]);
来说，也可以看作sell[i][j] = Math.max(sell[i-1][j],buy[i][j-1]+prices[i]);
这样是将i天完成了j-1次交易并又买入了股票，并在当天卖出，这样可以来状态压缩了。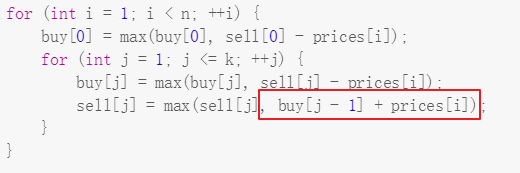
image.png

309. 最佳买卖股票时机含冷冻期

image.png
用 f[i]f[i] 表示第 i 天结束之后的「累计最大收益」
由于我们最多只能同时买入（持有）一支股票，并且卖出股票后有冷冻期的限制，因此我们会有三种不同的状态：

  1. 持有一只股票，对应的累计最大收益是f[i][0]
  2. 不持有股票，并且处于冷静期，对应的最大收益是f[i][1]
  3. 不持有股票，不处于冷静期，对应的最大收益是f[i][2]

这里的「处于冷冻期」指的是在第 i 天结束之后的状态。也就是说：如果第 ii 天结束之后处于冷冻期，那么第 i+1 天无法买入股票。
**

以上三种状态 ：

  1. 持有一只股票，对应的累计最大收益是f[i][0]
    1. 昨天买了股票，今天没有卖出f[i-1][0]
    2. 今天不是冷静期，并且买了股票 f[i-1][2]-price[i]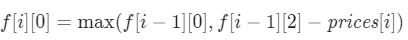
    3. image.png
  2. 不持有股票，并且处于冷静期，对应的最大收益是f[i][1]
    1. 今天卖了股票f[i-1][0] + price[i]
    2. image.png
  3. 不持有股票，不处于冷静期，对应的最大收益是f[i][2]
    1. 昨天没有股票，并且是冷冻期f[i-1][2]
    2. 昨天没有股票，并且不是冷冻期f[i-1][1]
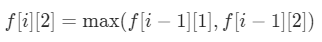
    3. image.png
  1. class Solution {
  2.     public int maxProfit(int[] prices) {
  3.         int len = prices.length;
  4.         if(len<=1)
  5.             return 0;
  6.         int[][] f = new int[len][3];
  7.         f[0][0] = -prices[0];
  8.         for(int i = 1; i < len; i++) {
  9.             f[i][0] = Math.max(f[i-1][0],f[i-1][2]-prices[i]);
  10.             f[i][1] = f[i-1][0]+prices[i];
  11.             f[i][2] = Math.max(f[i-1][1],f[i-1][2]);
  12.         }
  13.         return Math.max(f[len-1][2],f[len-1][1]);
  14.     }
  15. }

54. 螺旋矩阵

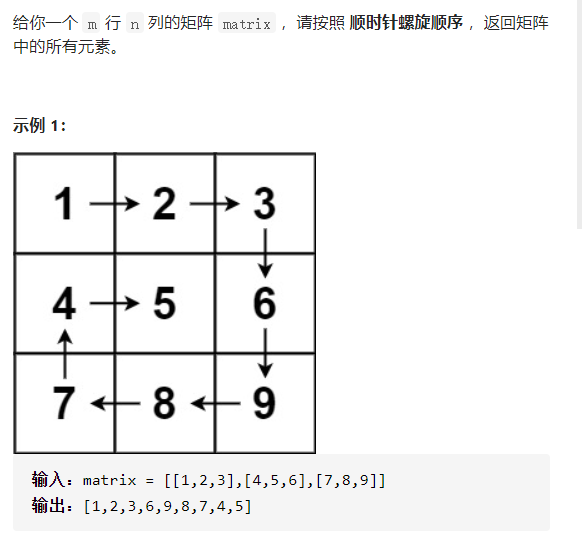
image.png

  • 每次遍历一圈，一圈结束时候指向开始的时候[up,left]，这个时候需要让i+1,j+1指向新的开始（例如上图第一圈开始的是0，0；第二圈开始的就是1，1了）

    1. class Solution {
    2.   public List<Integer> spiralOrder(int[][] matrix) {
    3.       List<Integer> res = new ArrayList();
    4.       int n = matrix.length;
    5.       if(n<=0) {
    6.           return res;
    7.       }
    8.       int m = matrix[0].length;
    9.       if(m<=0) {
    10.           return res;
    11.       }
    12.       int up = 0;
    13.       int down = n-1;
    14.       int left = 0;
    15.       int right = m-1;
    17.       int i = 0;
    18.       int j = 0;
    19.       while(true) {
    20.           // 第一行
    21.           while(j<=right){
    22.               res.add(matrix[i][j]);
    23.               j++;
    24.           } 
    25.           // 第一行最后j指向了right+1,所以需要j--，使其恢复
    26.           j--;
    27.           // 只有一行的时候，break就行了
    28.           if(up>=down){
    29.               break;
    30.           }
    31.           // 进入[up,right]的下一行[up+1,right]
    32.           i++;
    33.           while(i<=down){
    34.               res.add(matrix[i][j]);
    35.               i++;
    36.           }
    37.           i--; // i这个时候=down+1,需要--指向down
    38.           if(left>=right){
    39.               break;
    40.           }
    41.           j--;
    42.           while(j>=left){
    43.               res.add(matrix[i][j]);
    44.               j--;
    45.           }
    46.           j++;
    47.           i--;
    48.           while(i>up){
    49.               res.add(matrix[i][j]);
    50.               i--;
    51.           }
    52.           i++;j++;
    53.           up++;left++;
    54.           down--;right--;
    55.           if(up>down || left>right){
    56.               break;
    57.           }
    58.       }
    59.       return res;
    60.   }
    61. }

    124. 二叉树中的最大路径和

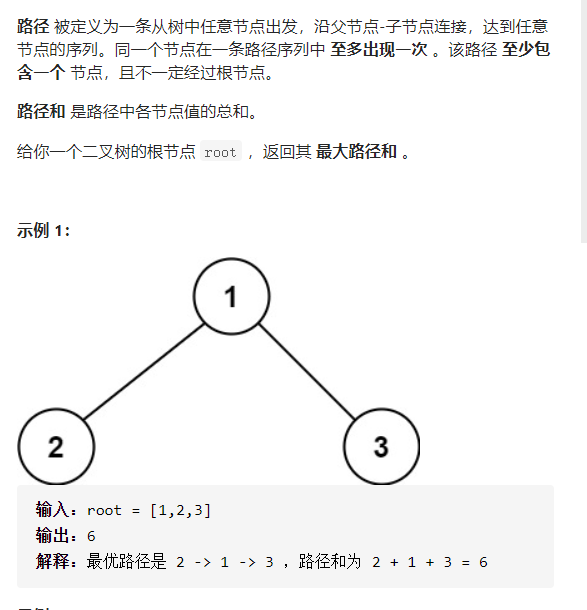
    image.png

  • 空节点的最大贡献值等于 00。

  • 非空节点的最大贡献值等于节点值与其子节点中的最大贡献值之和（对于叶节点而言，最大贡献值等于节点值）。

  • 对于二叉树中的一个节点，该节点的最大路径和取决于该节点的值与该节点的左右子节点的最大贡献值，如果子节点的最大贡献值为正，则计入该节点的最大路径和，否则不计入该节点的最大路径和。 ```java class Solution { int maxSum = Integer.MIN_VALUE;

    public int maxPathSum(TreeNode root) {

    1.   maxGain(root);
    2.   return maxSum;

    }

    public int maxGain(TreeNode node) {

    1.   if (node == null) {
    2.       return 0;
    3.   }
    5.   // 递归计算左右子节点的最大贡献值
    6.   // 只有在最大贡献值大于 0 时，才会选取对应子节点
    7.   int leftGain = Math.max(maxGain(node.left), 0);
    8.   int rightGain = Math.max(maxGain(node.right), 0);
    10.   // 节点的最大路径和取决于该节点的值与该节点的左右子节点的最大贡献值
    11.   int priceNewpath = node.val + leftGain + rightGain;
    13.   // 更新答案
    14.   maxSum = Math.max(maxSum, priceNewpath);
    16.   // 返回节点的最大贡献值
    17.   return node.val + Math.max(leftGain, rightGain);

    } }

  1. <a name="Dv5mF"></a>
  2. #### [105. 从前序与中序遍历序列构造二叉树](https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/)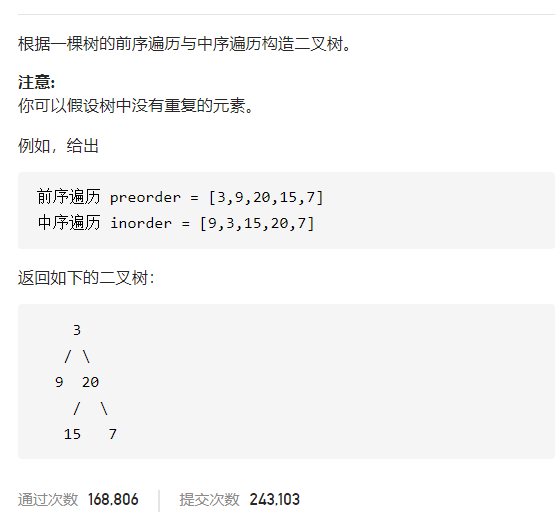
  3. ![image.png](https://cdn.nlark.com/yuque/0/2021/png/8429887/1616395033968-5ae9194a-3491-4d4a-82e7-1d09f468bfd4.png#align=left&display=inline&height=529&margin=%5Bobject%20Object%5D&name=image.png&originHeight=529&originWidth=558&size=23568&status=done&style=none&width=558)
  4. ```java
  5. class Solution {
  6.     public TreeNode buildTree(int[] preorder, int[] inorder) {
  7.         return build(preorder,inorder,0,preorder.length-1,0,inorder.length-1);
  8.     }
  10.     public TreeNode build(int[] preorder,int[] inorder,int pl,int pr,int il,int ir) {
  11.         if(pl==pr) {
  12.             return new TreeNode(preorder[pl]);
  13.         }
  14.         if(pl>pr)
  15.             return null;
  16.         int now = preorder[pl];
  17.         int pos = 0;
  18.         int index = il;
  19.         while(index<=ir) {
  20.             if(inorder[index]==now) {
  21.                 pos = index;
  22.                 break;
  23.             }
  24.             index++;
  25.         }
  26.         TreeNode root = new TreeNode(now);
  27.         root.left = build(preorder,inorder,pl+1,pl+pos-il,il,pos-1);
  28.         root.right = build(preorder,inorder,pl+pos-il+1,pr,pos+1,ir);
  29.         return root;
  30.     }
  31. }

93. 复原 IP 地址

image.png

  1. class Solution {
  2.     public List<String> restoreIpAddresses(String s) {
  3.         List<String> res = new ArrayList();
  4.         restore(s,res,new StringBuilder(),0,s.length(),0);
  5.         return res;
  6.     }
  8.     public void restore(String s,List<String> res,StringBuilder ip,int start,int len,int count) {
  9.         // start已经到达末尾，或者已经有了三个点
  10.         if(start==len || count==4) {
  11.             // 不满足其中一个要求，失败
  12.             if(start==len && count==4)
  13.                 res.add(ip.toString());
  14.             return;
  15.         }
  16.         // 不能含有前导 0，所以如果第一个数字是0，分成两个情况
  17.         int num = s.charAt(start)-'0';
  18.         if(num==0) {
  19.             // 当前整数只能为0
  20.             ip.append('0');
  21.             if(count!=3) {
  22.                 ip.append('.');
  23.             }
  24.             restore(s,res,ip,start+1,len,count+1);
  25.             if(count!=3) {
  26.                 ip.deleteCharAt(ip.length()-1);
  27.             }
  28.             ip.deleteCharAt(ip.length()-1);
  29.             return;
  30.         } else {
  31.             num = 0;
  32.             // 当前整数可以是1位，2位，3位的
  33.             for(int i = start;i < len;i++) {
  34.                 num = num * 10 + (s.charAt(i)-'0');
  35.                 // 符合条件
  36.                 if(num>0 && num<=255) {
  37.                     ip.append(num+"");
  38.                     if(count!=3) {
  39.                         ip.append('.');
  40.                     }
  41.                     restore(s,res,ip,i+1,len,count+1);
  42.                     if(count!=3) {
  43.                         ip.deleteCharAt(ip.length()-1);
  44.                     }
  45.                     int length = i-start+1;
  46.                     // 根据刚才加入数字的长度删除对应长度个
  47.                     while(length!=0) {
  48.                         ip.deleteCharAt(ip.length()-1);
  49.                         length--;
  50.                     }
  51.                 } else {
  52.                     return;
  53.                 }
  54.             }
  55.         }  
  56.     }
  57. }

22. 括号生成

image.png

  • n代表可以有n个左括号，n个右括号

  • 必须先有左括号再加右括号

    1. class Solution {
    2.   public List<String> generateParenthesis(int n) {
    3.       List<String> list = new ArrayList();
    4.       generate(list,new StringBuilder(),0,0,n);
    5.       return list;
    6.   }
    8.   // max = 最多左括号的数量
    9.   public void generate(List<String> list,StringBuilder builder,int open,int close,int max) {
    10.       if(builder.length()==2*max){
    11.           list.add(builder.toString());
    12.           return;
    13.       }
    14.       // 可以加左括号
    15.       if(open<max) {
    16.           builder.append("(");
    17.           generate(list,builder,open+1,close,max);
    18.           builder.deleteCharAt(builder.length()-1);
    19.       } 
    20.       // 右括号比左括号少，可以加右括号
    21.       if(close<open) {
    22.           builder.append(")");
    23.           generate(list,builder,open,close+1,max);
    24.           builder.deleteCharAt(builder.length()-1);
    25.       }
    26.   }
    27. }

    143. 重排链表

    image.png

  • 找到中点，reverse后半段

  • 将逆转后的后半段间隔插入到前半段```

    1. class Solution {
    2.   public void reorderList(ListNode head) {
    3.       int len = 0;
    4.       ListNode now = head;
    5.       while(now!=null) {
    6.           now = now.next;
    7.           len++;
    8.       }
    9.       if(len==1)
    10.           return;
    11.       len = (len+1)/2;
    12.       now = head;
    13.       while(len!=1) {
    14.           len--;
    15.           now = now.next;
    16.       }
    17.       ListNode now2 = now.next;  // 找到后半段
    18.       now.next = null;
    19.       now = head;
    21.       // 反转后半段
    22.       ListNode dummy = new ListNode(-1);
    23.       dummy.next = now2;
    24.       now2 = reverse(dummy);
    26.       // 间隔插入
    27.       while(now2!=null) {
    28.           ListNode nex = now.next;
    29.           ListNode nex2 = now2.next;
    30.           now.next = now2;
    31.           now2.next = nex;
    32.           now = nex;
    33.           now2 = nex2;
    34.       }
    35.   }
    37.   ListNode reverse(ListNode dummy) {
    38.       ListNode now = dummy.next.next;
    39.       dummy.next.next = null;
    40.       while(now!=null) {
    41.           ListNode t = now.next;
    42.           now.next = dummy.next;
    43.           dummy.next = now;
    44.           now = t;
    45.       }
    46.       return dummy.next;
    47.   }
    48. }