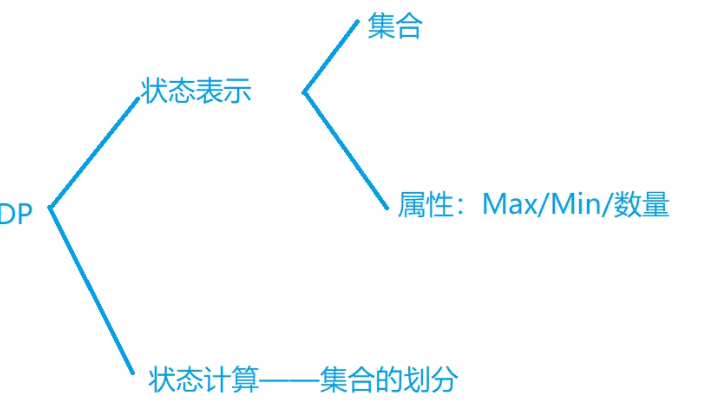
分析过程

最大子和

image.png

image.png
分析:

  • 以f[i]结尾的序列,它所代表的最大值是
    • f(i-1)+f(i)
    • f(i-2)+f(i-1)+f(i)
    • …
    • f(1)+……+f(i-2)+f(i-1)+f(i)
  • 如果他们同时减去f(i)那么值是不变的,所以就可以只考虑
    • f(i-1)
    • f(i-2)+f(i-1)
    • …
    • f(1)+……+f(i-2)+f(i-1)
  • 的最大值
  • 同时这个时候已经确保了s(i-1)为i-1为最后一个元素的最大值,所以只需要max(s(i-1),0)+f(i)

三角形

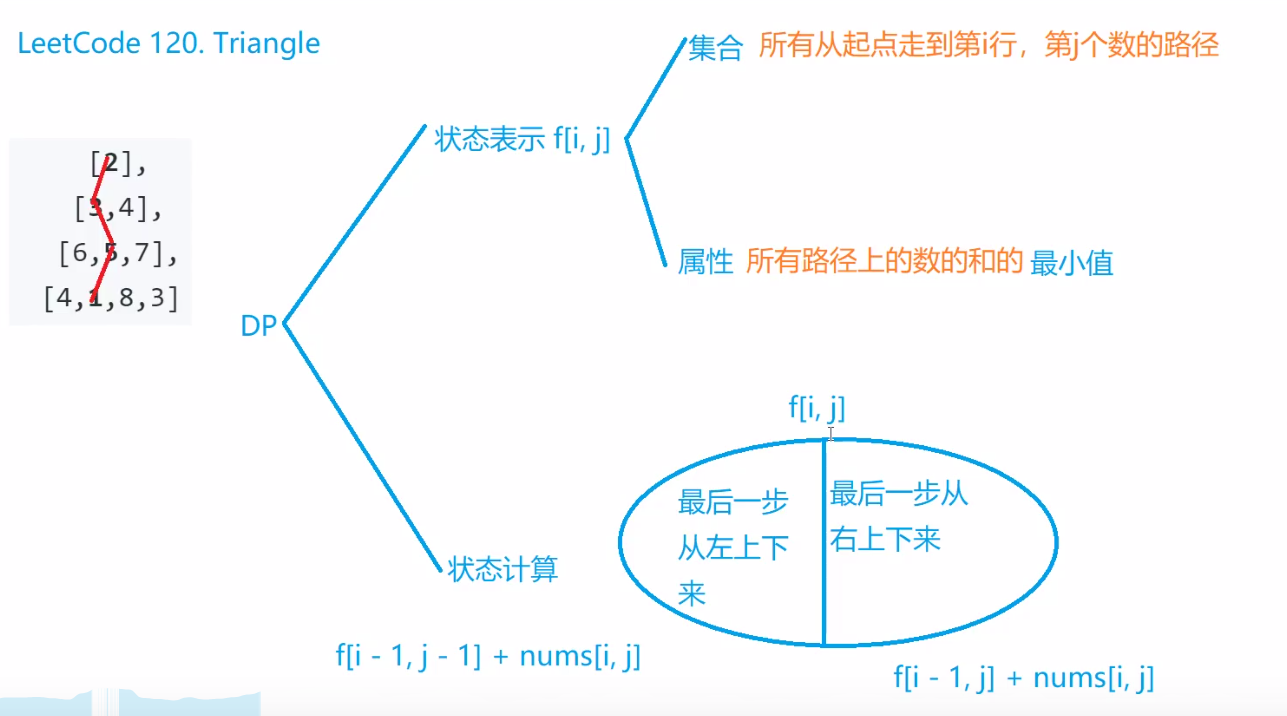
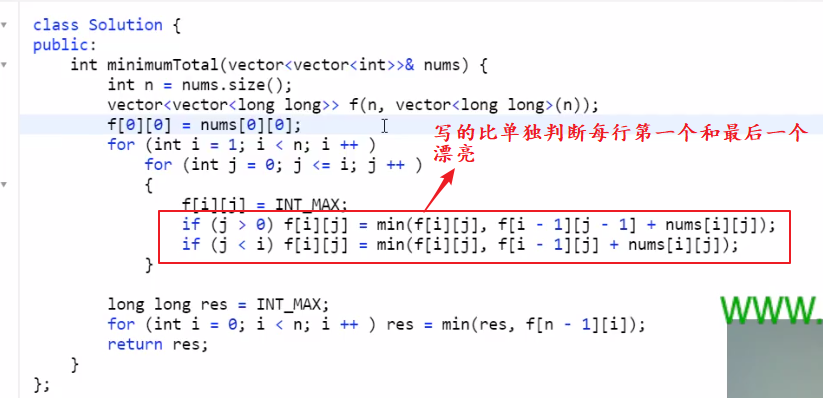
image.png
image.png
image.png

解码字母

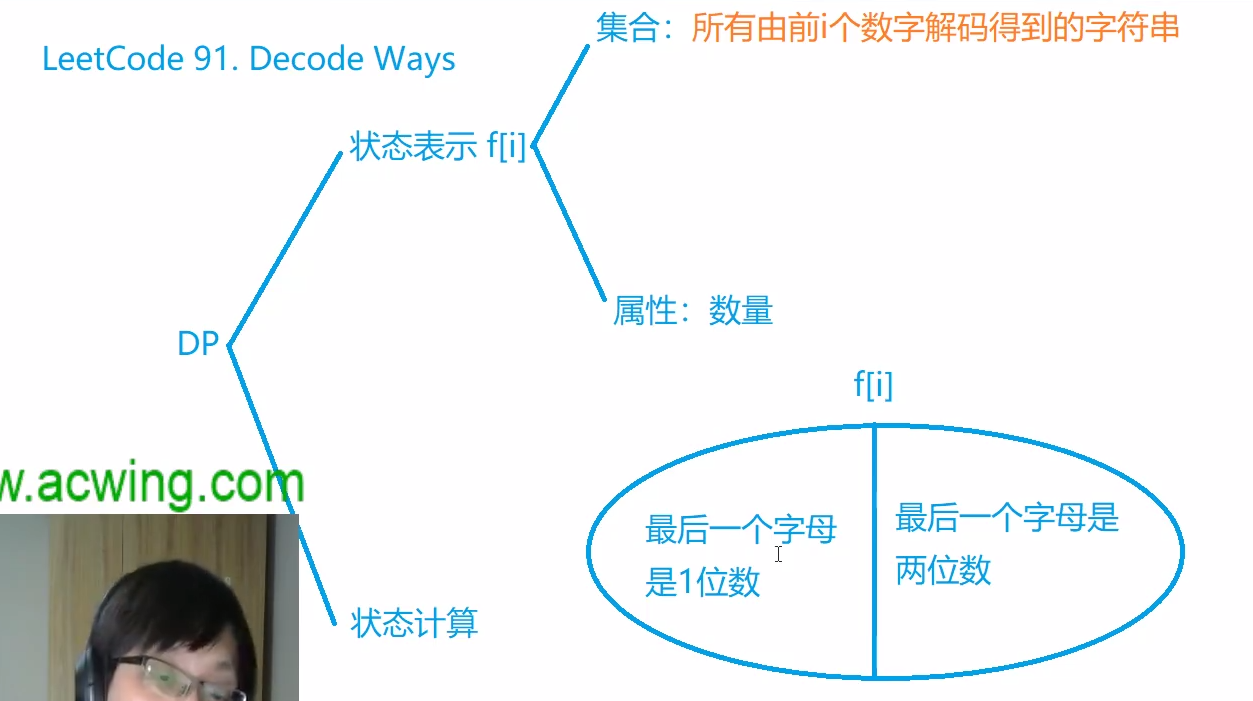
image.png

image.png

image.png

题目

32. 最长有效括号image.png

“….) )”+”…..( )”
https://leetcode-cn.com/problems/longest-valid-parentheses/solution/zui-chang-you-xiao-gua-hao-by-leetcode-solution/

300. 最长递增子序列

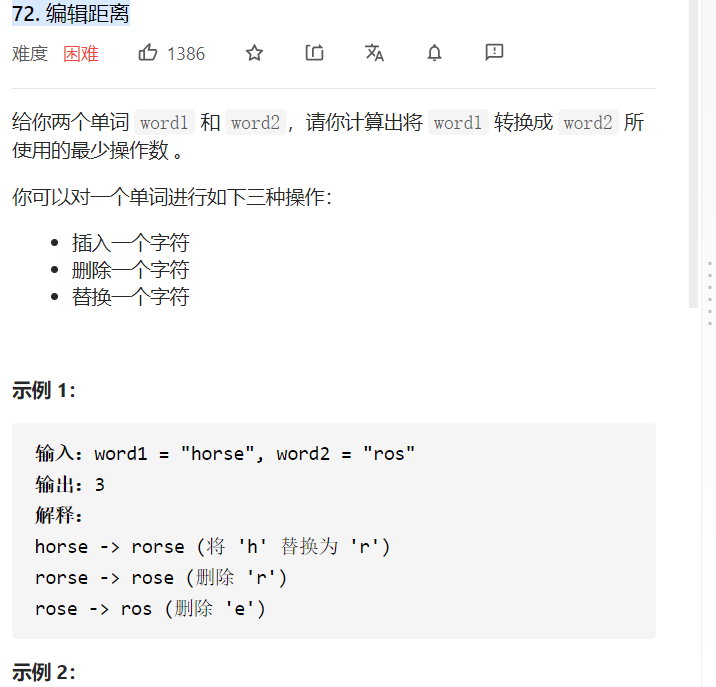
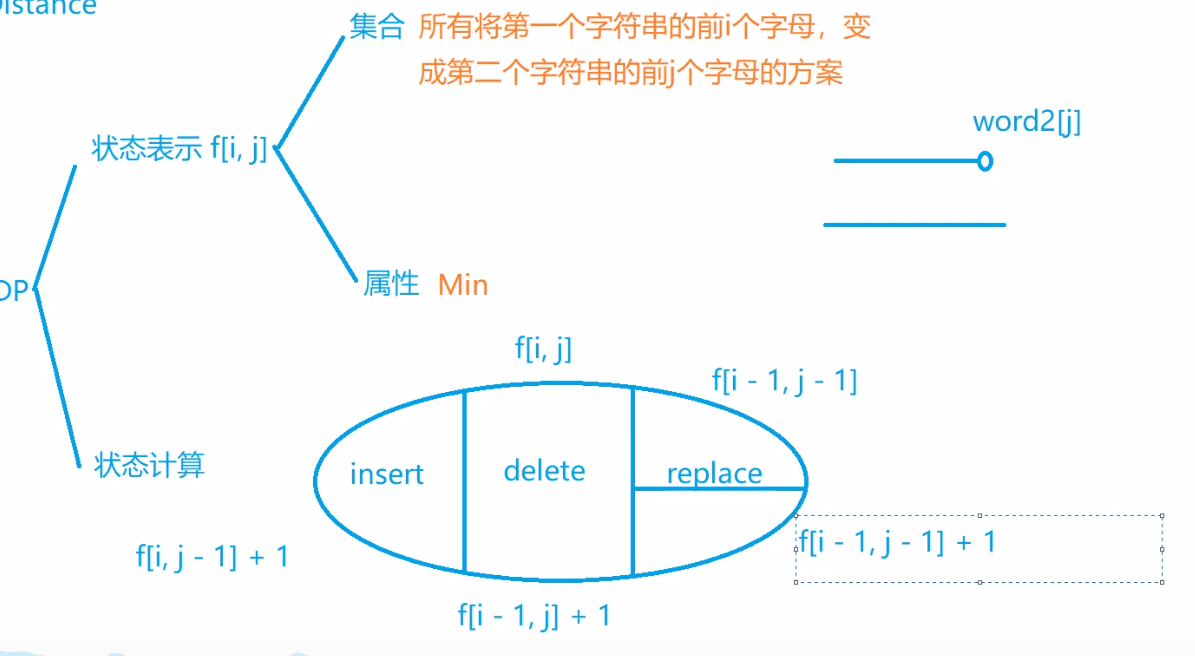
image.png

72. 编辑距离

image.png
image.png

518. 零钱兑换 II

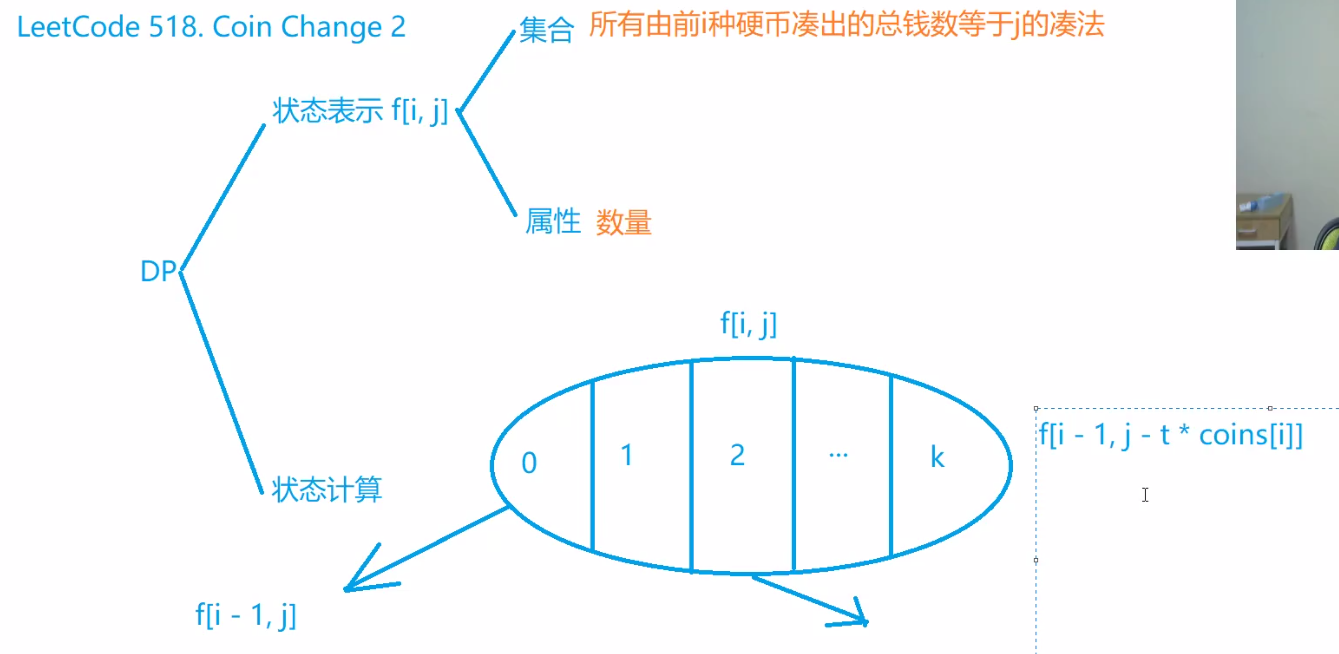
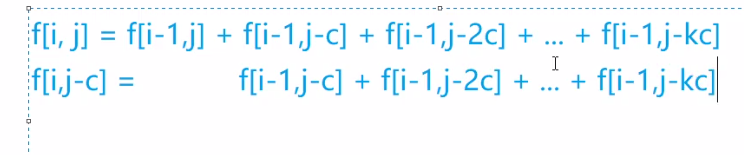
image.png
image.png
image.png

  1. class Solution {
  2.     public int change(int amount, int[] coins) {
  3.         int m = coins.length;
  4.         int[] dp = new int[amount+1];
  5.         dp[0] = 1; 
  6.         for(int coin:coins) {
  7.             // j =coin  代表从使用一个coin开始
  8.             for(int j = coin; j <= amount; j ++) {
  9.                 dp[j] += dp[j-coin];  
  10.             }
  11.             for(int j = 0 ; j <= amount; j++) {
  12.                 System.out.print(dp[j]+" ");
  13.             }
  14.             System.out.println();
  15.         }
  16.         return dp[amount];
  17.     }
  18. }

image.png

664. 奇怪的打印机

image.png

  1. 第一种：dp[i][j] = 1 + dp[i + 1][j];//i单独打印， s[i + 1, j]段另外打印
  3. //dp[i + 1][k]代表将i放到[i+ 1, k]一起打印，dp[k + 1][j]代表[k + 1, j]另外打印，（s[i] == s[k])
  4. 第二种：dp[i][j] = min(dp[i][j], dp[i + 1][k] + dp[k + 1][j]);
  6. //dp[i + 1][j]代表将i放入[j + 1, i]一起打印(s[i] == s[j])
  7. 第三种：dp[i][j] = min(dp[i][j], dp[i + 1][j]);

1.png

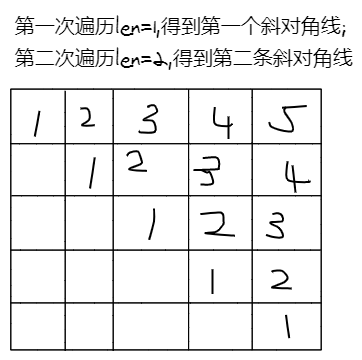
  1. class Solution {
  2.     public int strangePrinter(String s) {
  3.         int n = s.length();
  4.         if(n==0)
  5.             return 0;
  6.         int[][] dp = new int[n+1][n+1];
  7.         for(int i = 0 ; i < n; i++) {
  8.             dp[i][i] = 1;
  9.         }
  10.         for(int len = 2; len <= n ; len ++) {
  11.             for(int l = 0 ; l + len -1 < n ; l++) {
  12.                 int r = l  +len-1;
  13.                 dp[l][r] = 1 + dp[l+1][r];  // 初始化为s[i]是画完[l+1,r]以后再画的
  14.                 for(int k = l+1 ;k <= r;k++) {
  15.                     if(s.charAt(k)==s.charAt(l)) {
  16.                         dp[l][r] = Math.min(dp[l][r],dp[l+1][k]+dp[k+1][r]);  // 以k为分界线,s[i]与s[k]假设是被一笔画出的
  17.                     }
  18.                 }
  19.                 // if(s.charAt(l)==s.charAt(r)) dp[l][r] = Math.min(dp[l][r],dp[l+1][r]);
  20.             }
  21.         }
  22.         return dp[0][n-1];
  23.     }
  24. }

10. 正则表达式匹配

image.png
2.png

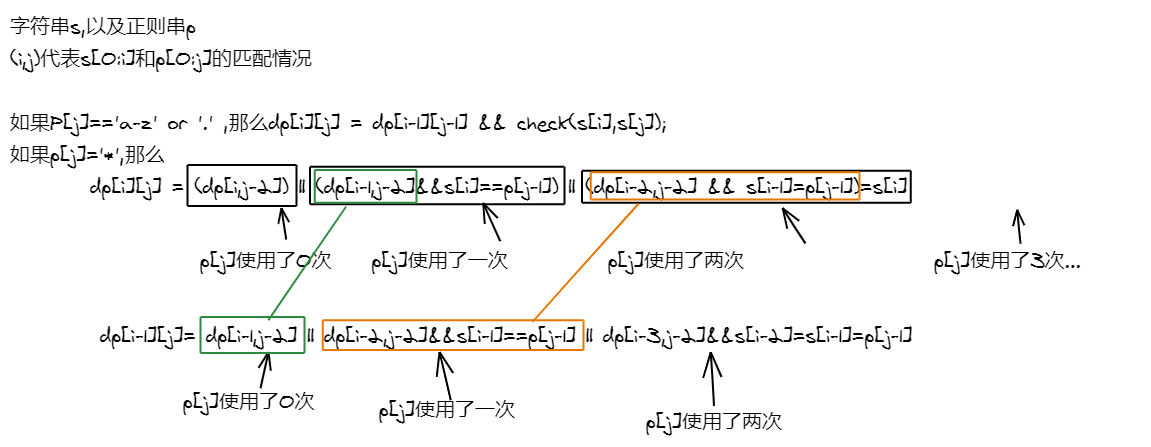
  1. class Solution {
  2.     public boolean isMatch(String s, String p) {
  3.         int m = s.length();
  4.         int n = p.length();
  6.         boolean[][] dp = new boolean[m+1][n+1];
  7.         dp[0][0] = true;
  9.         for(int i = 1; i+1 <= n ; i+=2) { // a*b*c的情况
  10.             if(p.charAt(i)=='*') {
  11.                 dp[0][i+1] = true;
  12.             } else {
  13.                 break;
  14.             }
  15.         }
  16.         for(int i = 1; i <= m; i ++) {
  17.             for(int j = 1 ; j <= n ; j++) {
  18.                 if(p.charAt(j-1)=='.') {
  19.                     // 注意要&&dp[i-1][j-1]
  20.                     dp[i][j] = true && dp[i-1][j-1];
  21.                 } else if(p.charAt(j-1)=='*') {
  22.                     dp[i][j] = dp[i-1][j] && check(s.charAt(i-1),p.charAt(j-2));
  23.                     if(j>=2)
  24.                         dp[i][j] = dp[i][j] || dp[i][j-2];
  25.                     // dp[i][j] = dp[i][j-2] || (dp[i-1][j] && s.charAt(i)==p.charAt(j-1));
  26.                 } else {
  27.                     if(s.charAt(i-1) == p.charAt(j-1))
  28.                         // 注意要&&dp[i-1][j-1]
  29.                         dp[i][j] = true && dp[i-1][j-1];  
  30.                 }
  31.             }
  32.         }
  34.         return dp[m][n];
  35.     }
  37.     boolean check(char a,char b) {
  38.         if(b=='.')
  39.             return true;
  40.         if(a==b)
  41.             return true;
  43.         return false;
  44.     }
  45. }