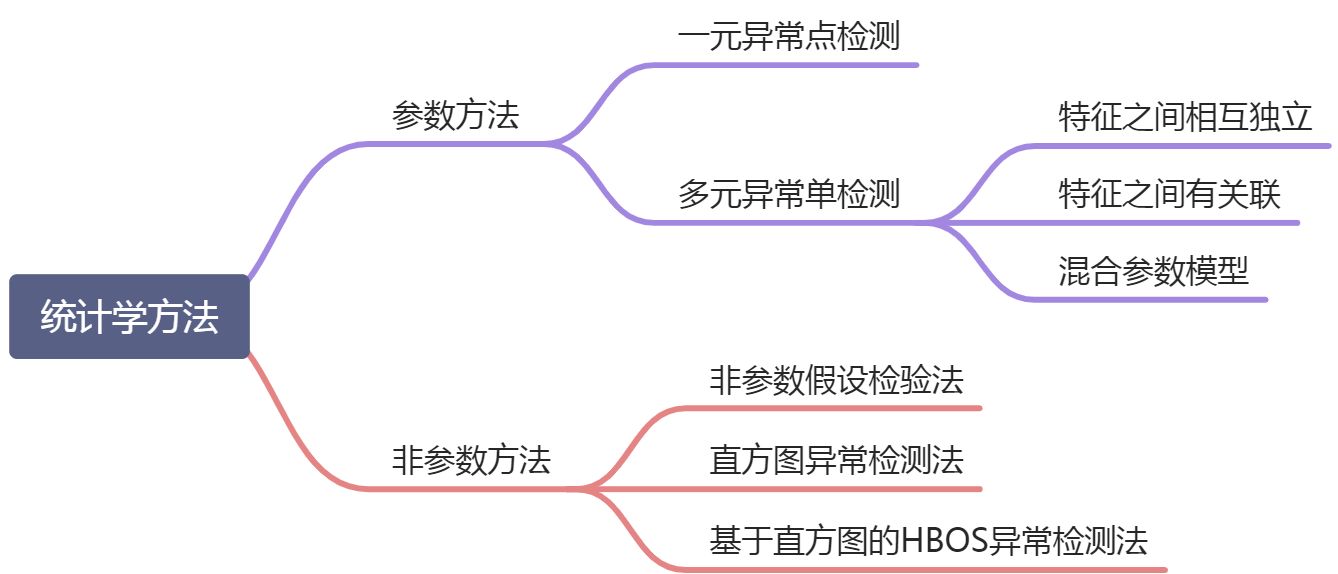
内容概要： Task02：基于统计学的方法 - 图1

1. 概述

统计学方法对数据的正常性做出假定。它们假定正常的数据对象由一个统计模型产生，而不遵守该模型的数据是异常点。统计学方法的有效性高度依赖于对给定数据所做的统计模型假定是否成立。

异常检测的统计学方法的一般思想是：学习一个拟合给定数据集的生成模型，然后识别该模型低概率区域中的对象（通常会设定一个阈**值ε），把它们（低于阈值的对象）作为异常点**。
即利用统计学方法建立一个模型，然后考虑对象有多大可能符合该模型。

根据如何指定和学习模型，异常检测的统计学方法可以划分为两个主要类型：参数方法和非参数方法。

  • 参数方法：假定正常的数据对象被一个以Task02：基于统计学的方法 - 图2为参数的参数分布产生。该参数分布的概率密度函数Task02：基于统计学的方法 - 图3#card=math&code=f%28x%2C%5CTheta%29)给出对象Task02：基于统计学的方法 - 图4被该分布产生的概率。该值越小，Task02：基于统计学的方法 - 图5越可能是异常点。


  • 非参数方法：并不假定先验统计模型，而是试图从输入数据确定模型。非参数方法通常假定参数的个数和性质都是灵活的，不预先确定（所以非参数方法并不是说模型是完全无参的，完全无参的情况下从数据学习模型是不可能的）。


2. 参数方法

2.1 基于正态分布的一元异常点检测

仅涉及一个属性或变量的数据称为一元数据。我们假定数据由正态分布产生，然后可以由输入数据学习正态分布的参数，并把低概率的点识别为异常点。

假定输入数据集Task02：基于统计学的方法 - 图6，数据集中的样本服从正态分布，即Task02：基于统计学的方法 - 图7，我们可以根据样本求出参数Task02：基于统计学的方法 - 图8和Task02：基于统计学的方法 - 图9。求解公式如下：
Task02：基于统计学的方法 - 图10%7D#card=math&code=%5Cmu%3D%5Cfrac%201m%5Csum_%7Bi%3D1%7D%5Em%20x%5E%7B%28i%29%7D)

  1.         ![](https://g.yuque.com/gr/latex?%5Csigma%5E2%3D%5Cfrac%201m%5Csum_%7Bi%3D1%7D%5Em%20(x%5E%7B(i)%7D-%5Cmu)%5E2#card=math&code=%5Csigma%5E2%3D%5Cfrac%201m%5Csum_%7Bi%3D1%7D%5Em%20%28x%5E%7B%28i%29%7D-%5Cmu%29%5E2)

求出参数之后，我们就可以根据概率密度函数计算数据点服从该分布的概率。正态分布的概率密度函数为：
Task02：基于统计学的方法 - 图11%3D%5Cfrac%201%7B%5Csqrt%7B2%5Cpi%7D%5Csigma%7Dexp(-%5Cfrac%7B(x-%5Cmu)%5E2%7D%7B2%5Csigma%5E2%7D)#card=math&code=p%28x%29%3D%5Cfrac%201%7B%5Csqrt%7B2%5Cpi%7D%5Csigma%7Dexp%28-%5Cfrac%7B%28x-%5Cmu%29%5E2%7D%7B2%5Csigma%5E2%7D%29)

如果计算出来的概率低于阈值，就可以认为该数据点为异常点。

阈值是个经验值，可以选择在验证集上使得评估指标值最大（也就是效果最好）的阈值取值作为最终阈值。

例如常用的3sigma原则（又叫拉依达准则，pauta criterion）中，如果数据点超过范围Task02：基于统计学的方法 - 图12，那么这些点很有可能是异常点。
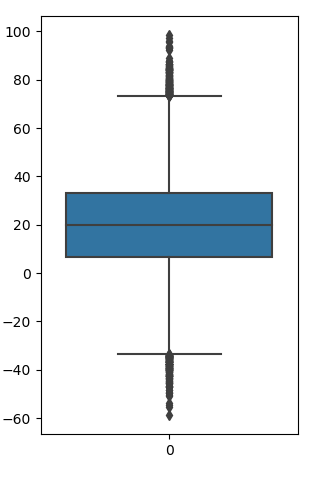
这个原则在可视化中通常使用箱线图进行展示。箱线图对数据分布做了一个简单的统计可视化，利用数据集的上下四分位数（Q1和Q3）、中点等形成。异常点常被定义为小于Q1－1.5IQR或大于Q3+1.5IQR的那些数据。

例子：
用Python画一个简单的箱线图：

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

data = np.random.randn(50000) * 20 + 20
sns.boxplot(data=data)
plt.show()

image.png

拓展资料：
在检测异常值使用的准则常见的有拉伊达 ( PauTa)准则、格拉布斯 ( Grubbs)准则、肖维纳 (Chauvenet)准则、狄克逊Dixon Criterion准则等。

①拉伊达准则是以三倍测量列的标准偏差为极限取舍标准,其给定的置信概率为99.73%,该 准则适用于测量次数n>10或预先经大量重复测量已统计出其标准误差σ的情况。Xi为服从正态分布的等精度测量值,可先求得它们的算术平均值 X、残差vi和标准偏差σ。 若|Xi- X|>3σ,则可疑值Xi含有粗大误差,应舍弃; 若|Xi- X|≤3σ,则可疑值Xi为正常值,应保留。 把可疑值舍弃后再重新算出除去这个值的其他测量值的平均值和标准偏差,然后继续使用判别依据判断,依此类推。

②格拉布斯准则 格拉布斯准则适用于测量次数较少的情况(n<100),通常取置信概率为95%,对样本中仅混入一个异常值的情况判别效率最高。其判别方法如下: 先将呈正态分布的等精度多次测量的样本按从小到大排列,统计临界系数G(a,n)的值为G0, 然后分别计算出G1、Gn:G1=(X-X1)/σ,Gn=(Xn- X)/σ。若G1≥Gn且G1>G0,则X1应予以剔除; 若Gn≥G1且Gn>G0,则Xn应予以剔除; 若G1<G0且Gn<G0,则不存在“坏值”。 然后用剩下的测量值重新计算平均值和标准偏差,还有G1、Gn和G0,重复上述步骤继续进行 判断,依此类推。

③肖维勒准则 肖维勒准则是建立在频率p=m/n趋近于概率P{|Xi- X|>Zcσ}的前提下的(其中m是绝对值大于Ecσ的误差出现次数,P是置信概率)。设等精度且呈正态分布的测量值为Xi,若其残差vi≥Zcσ则Xi可视为含有粗大误差,此时把读数Xi应舍弃。把可疑值舍弃后再重新计算和继续使用判别依据判断,依此类推。

④狄克逊准则 狄克逊准则是一种用极差比双侧检验来判别粗大误差的准则。它从测量数据的最值入手,一般取显著性水平a为0.01.此准则的特点是把测量数据划分为四个组,每个组都有相应的极端异常值统计量R1、R2的计算方法,再根据测量次数n和所对应的统计临界系数D(a,n)按照以下方法来判别: 若R1>R2,R1>D(a,n),则判别X1为异常值,应舍弃; 若R2>R1,R2>D(a,n),则应舍弃Xn

资料来源： 百度文库——粗大误差四种判别准则的比较：https://wenku.baidu.com/view/74f2b02189eb172dec63b7ba.html 百度百科——拉依达准则：https://baike.baidu.com/item/%E6%8B%89%E4%BE%9D%E8%BE%BE%E5%87%86%E5%88%99


2.2 多元异常点检测

涉及两个或多个属性或变量的数据称为多元数据。

2.2.1 基于一元拓展到多元

许多一元异常点检测方法都可以扩充，用来处理多元数据。其核心思想是把多元异常点检测任务转换成一元异常点检测问题。例如基于正态分布的一元异常点检测扩充到多元情形时，可以通过求出每一维度的均值和标准差，继而求出数据点在每一维度的概率，同时根据联合概率分布的性质，可以计算该数据点的总体概率值，最后根据预先设定的阈值 Task02：基于统计学的方法 - 图14 来判断该数据点是否异常。

对于给定的数据集 Task02：基于统计学的方法 - 图15，每一个样本 Task02：基于统计学的方法 - 图16 ，假设 Task02：基于统计学的方法 - 图17 服从高斯分布，即Task02：基于统计学的方法 - 图18，我们对每一个特征（这里选择的特征是与异常具有相关属性的特征）计算均值 Task02：基于统计学的方法 - 图19 和 方差Task02：基于统计学的方法 - 图20 ：

Task02：基于统计学的方法 - 图21%7D#card=math&code=%5Cmuj%3D%5Cfrac%201m%5Csum%7Bi%3D1%7D%5Em%20x_j%5E%7B%28i%29%7D)

        ![](https://g.yuque.com/gr/latex?%5Csigma_j%5E2%3D%5Cfrac%201m%5Csum_%7Bi%3D1%7D%5Em%20(x_j%5E%7B(i)%7D-%5Cmu_j)%5E2#card=math&code=%5Csigma_j%5E2%3D%5Cfrac%201m%5Csum_%7Bi%3D1%7D%5Em%20%28x_j%5E%7B%28i%29%7D-%5Cmu_j%29%5E2)

获得均值和方差之后，对于给定的一个新的样本 Task02：基于统计学的方法 - 图22 ，我们根据模型计算 Task02：基于统计学的方法 - 图23：

Task02：基于统计学的方法 - 图24

其中n为特征的数量。
这里计算Task02：基于统计学的方法 - 图25的方法为通过分别计算每个特征的概率值Task02：基于统计学的方法 - 图26然后将其累乘，从而得到最终的 Task02：基于统计学的方法 - 图27。
我们将 Task02：基于统计学的方法 - 图28 作为判定边界，当 Task02：基于统计学的方法 - 图29 则判断为该测试样本为异常样本；当 Task02：基于统计学的方法 - 图30 则判断该测试样本为正常样本。

这是在各个维度的特征之间相互独立的情况下。如果特征之间有相关性，就要用到多元高斯分布了。

例子：
以两个特征为例，看一下算法实现的形式。

  • 关于检测模型：这里我们假设该数据集包含2个维度 Task02：基于统计学的方法 - 图31，每一个维度 Task02：基于统计学的方法 - 图32 ，假设 Task02：基于统计学的方法 - 图33 服从高斯分布，且Task02：基于统计学的方法 - 图34 。
  • 关于待检测的数据集：我们这里生成符合正态分布的2个样本，样本容量都为20，用来模拟数据集的2个维度。

关键点一： 如何生成模型？
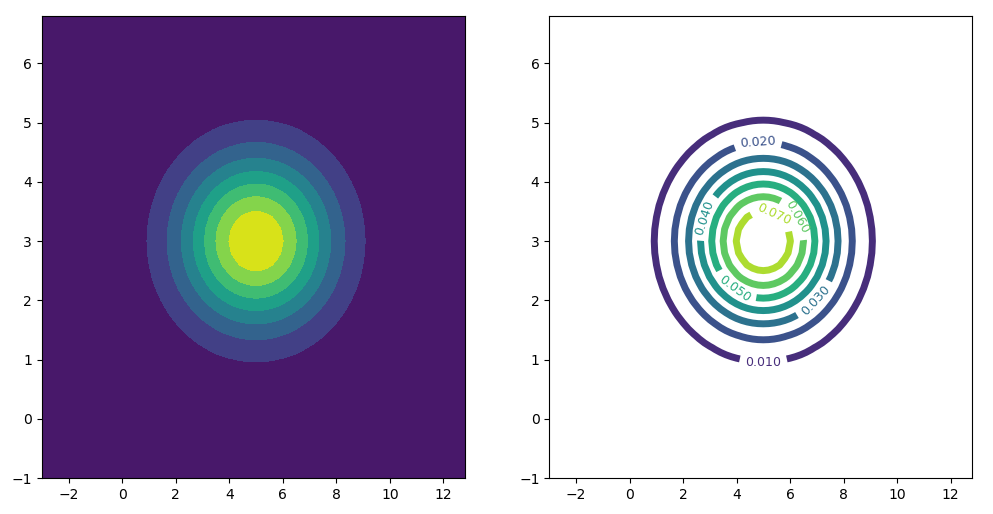
为了直观理解，我们把数据的2个维度，放到平面直角坐标系中，用坐标轴上的2个轴代表了模型的2个维度，而坐标轴上每一个坐标点代入到前面的 Task02：基于统计学的方法 - 图35 中可以计算每一个坐标点的概率，将每一个坐标点的概率作为模型的概率。

以下我们通过热力图来表现不同坐标点的概率值。

import matplotlib.pyplot as plt
import numpy as np 
from scipy.stats import norm

mean_1, theta_1 = 5, 2
mean_2, theta_2 = 3, 1
X = np.arange(mean_1-4*theta_1, mean_1+4*theta_1, 0.2)
Y = np.arange(mean_2-4*theta_2, mean_2+4*theta_2, 0.2)
X, Y = np.meshgrid(X, Y)

P_X = norm.pdf(X, loc=mean_1, scale=theta_1)
P_Y = norm.pdf(Y, loc=mean_2, scale=theta_2)
P = P_X * P_Y
fig, axs = plt.subplots(1, 2, figsize=(12, 6), sharey=True)
cs1 = axs[0].contourf(X, Y, P)
cs2 = axs[1].contour(X, Y, P, linewidths=5)  # 设置等高线线宽
axs[1].clabel(cs2, fontsize=9, inline=1)  # 设置显示等高线的值
plt.show()

image.png

关键点二：如何确定和设置阈值** Task02：基于统计学的方法 - 图37 **？
在网上查了很久，可能是查询方向不对，并没有查到具体的多元异常检测阈值的设置方法。
我自己的2个思路是：①从模型本身入手；②沿用前面一元异常点检测的阈值设置方法（或者是根据假设检验中的α值来确定）。

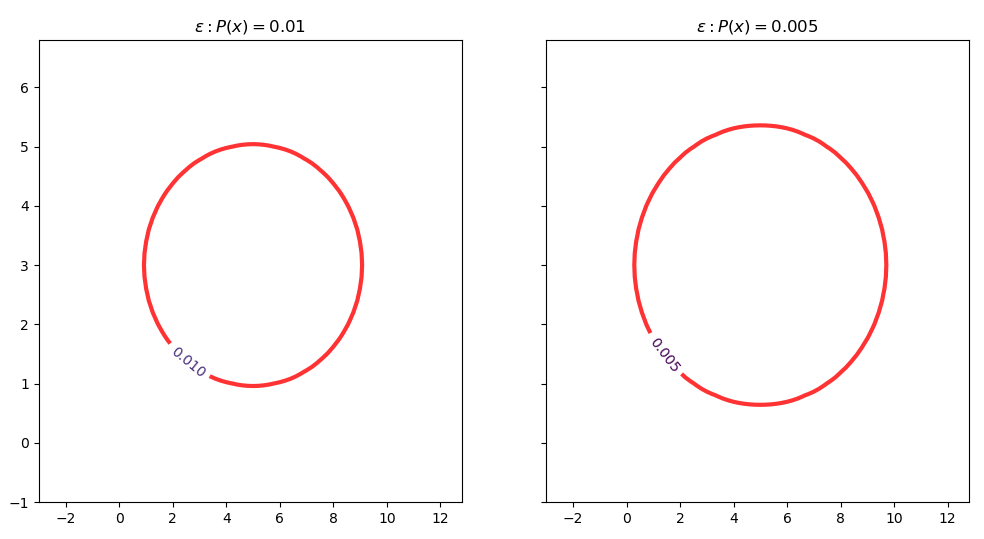
思路①：先看上面右边的图，从外往里数第二个等高线的值为0.01（第一个等高线的值是0），这个其实刚好对应3sigma原则，因为正态分布99%的值都落在3sigma内。此时我们设置阈值 Task02：基于统计学的方法 - 图38 。

思路②：使用假设检验的方法。H0: Task02：基于统计学的方法 - 图39 为正常值，H1：Task02：基于统计学的方法 - 图40 为异常值，显著性水平为α=0.5% 。此时Task02：基于统计学的方法 - 图41就是我们的阈值 Task02：基于统计学的方法 - 图42 。

我们可以改进前面的等高线图，画出这个边界：

fig, axs = plt.subplots(1, 2, figsize=(12, 6), sharey=True)
cs3 = axs[0].contour(X, Y, P, linewidths=0)  # 不显示等高线
plt.setp(cs3.collections[1], lw=3, color='red', alpha=0.8)  # 对指定等高线进行设置
manual_locations = [(cs3.levels[1], cs3.levels[-1])]  # 设置不显示等高线的范围
axs[0].clabel(cs3, inline=1, fontsize=10, manual=manual_locations)
axs[0].set_title('${\epsilon}:P(x)=0.01$')

cs4 = axs[1].contour(X, Y, P, [0, 0.005, 0.1, 0.5, 1], linewidths=0)  # 自定义等高线的值
plt.setp(cs4.collections, lw=3, color='red', alpha=0.8)
axs[1].clabel(cs4, inline=1, fontsize=10, manual=[(0.005, 1)])
axs[1].set_title('$\epsilon:P(x)=0.005$')
plt.show()

image.png

最后，我们再生成一个2维数据来进行检测：

data = norm.rvs(loc=(mean_1+mean_2)/2, scale=(theta_1+theta_2)/2,
                size=(2, 20), random_state=2021)

plt.figure()
ContourSet = plt.contour(X, Y, P, [0, 0.005, 0.1], linewidths=0) 
plt.setp(ContourSet.collections[1], lw=3, color='red', alpha=0.8)
manual_locations = [(ContourSet.levels[1], ContourSet.levels[-1])]

fmt = {}
strs = [None, '$\epsilon=0.005$', None]
for l, s in zip([0, 0.005, 0.1], strs):
    fmt[l] = s
plt.clabel(ContourSet, inline=1, fontsize=10, manual=manual_locations, fmt=fmt)
plt.text(mean_1, mean_2, "$p(x)>\epsilon$", fontsize=12, 
        bbox={'facecolor': 'c', 'alpha': 0.2, 'pad': 2} )
plt.text(5*theta_1, 5*theta_2, "$p(x)<\epsilon$", fontsize=12,
        bbox={'facecolor': 'r', 'alpha': 0.2, 'pad': 2} )
plt.scatter(data[0], data[1], marker='x')
plt.xlabel(r"$x_1$", size=15)
plt.ylabel(r"$x_2$", size=15)
plt.title("Anomaly detection based on Independently Multivariate Normal Distribution")
plt.show()

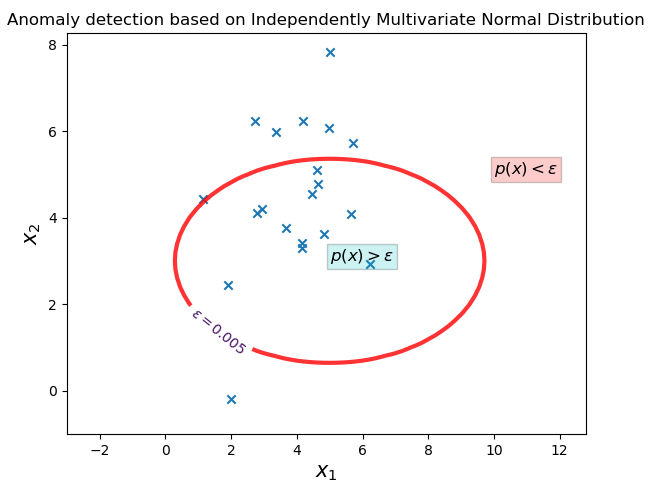
image.png

以上是通过可视化直观判断的方法。如果是进行预测的话，只需要计算样本各点的概率值，再和阈值做比较便可以得出各点的异常情况。

# mean_1, theta_1 = 5, 2
# mean_2, theta_2 = 3, 1
# data = norm.rvs(loc=(mean_1+mean_2)/2, scale=(theta_1+theta_2)/2,
#                 size=(2, 20), random_state=2021)
P_X1 = norm.pdf(data[0], loc=mean_1, scale=theta_1)
P_X2 = norm.pdf(data[1], loc=mean_2, scale=theta_2)
P = P_X1 * P_X2
label_ = (P<0.005).astype(np.int8)  # 异常点的预测值为1，正常点的预测值为0
print('异常样本点：\n{}'.format(data[:, label_==1]))

异常样本点： [[ 5.01401631 3.37232295 5.69628739 4.96750275 4.18631027 2.74306981 1.13841641 1.99569105] [ 7.8173719 5.97593668 5.72085398 6.06439114 6.22766189 6.22364837 4.41834064 -0.19029586]]

参考资料：

  • 斯坦福大学机器学习笔记——异常检测算法（高斯分布、多元高斯分布、异常检测算法）:

https://blog.csdn.net/wyl1813240346/article/details/79059647?depth_1-

  • 到底谁是异常 (多元高斯分布异常点检测)

https://blog.csdn.net/chikily_yongfeng/article/details/105750861?depth_1-

  • Matplotlib——Contour Demo:

https://matplotlib.org/3.1.1/gallery/images_contours_and_fields/contour_demo.html#sphx-glr-gallery-images-contours-and-fields-contour-demo-py


2.2.2 多个特征相关，且符合多元高斯分布

对于给定的数据集 Task02：基于统计学的方法 - 图45，每一个样本 Task02：基于统计学的方法 - 图46 ，假设 Task02：基于统计学的方法 - 图47 服从高斯分布，即Task02：基于统计学的方法 - 图48，且样本之间存在相关性，此时我们要求的参数变成了样本均值和协方差矩阵。

均值为：
Task02：基于统计学的方法 - 图49%7D#card=math&code=%5Cmu%3D%5Cfrac%7B1%7D%7Bm%7D%5Csum%5Em_%7Bi%3D1%7Dx%5E%7B%28i%29%7D)

协方差矩阵为：
Task02：基于统计学的方法 - 图50%7D-%5Cmu)(x%5E%7B(i)%7D-%5Cmu)%5ET#card=math&code=%5Csum%3D%5Cfrac%7B1%7D%7Bm%7D%5Csum%5Em_%7Bi%3D1%7D%28x%5E%7B%28i%29%7D-%5Cmu%29%28x%5E%7B%28i%29%7D-%5Cmu%29%5ET&height=49&width=241)

概率密度函数为：
Task02：基于统计学的方法 - 图51%3D%5Cfrac%7B1%7D%7B(2%20%5Cpi)%5E%7B%5Cfrac%7Bn%7D%7B2%7D%7D%7C%5CSigma%7C%5E%7B%5Cfrac%7B1%7D%7B2%7D%7D%7D%20%5Cexp%20%5Cleft(-%5Cfrac%7B1%7D%7B2%7D(x-%5Cmu)%5E%7BT%7D%20%5CSigma%5E%7B-1%7D(x-%5Cmu)%5Cright)#card=math&code=p%28x%29%3D%5Cfrac%7B1%7D%7B%282%20%5Cpi%29%5E%7B%5Cfrac%7Bn%7D%7B2%7D%7D%7C%5CSigma%7C%5E%7B%5Cfrac%7B1%7D%7B2%7D%7D%7D%20%5Cexp%20%5Cleft%28-%5Cfrac%7B1%7D%7B2%7D%28x-%5Cmu%29%5E%7BT%7D%20%5CSigma%5E%7B-1%7D%28x-%5Cmu%29%5Cright%29&height=54&width=362)

其中 Task02：基于统计学的方法 - 图52 为协方差矩阵的行列式。

对于多元高斯分布模型，需要有样本的数量m大于特征的数量n，否则协方差矩阵不可逆，通常需要Task02：基于统计学的方法 - 图53，另外特征的冗余也会导致协方差矩阵不可逆；而原来的高斯分布模型在m很小的情况下同样适用。

当协方差矩阵不可逆也就是协方差矩阵是奇异矩阵，通常有两种情况产生：
1. 没有满足Task02：基于统计学的方法 - 图54。
2. 有多余的特征，也就是说可能两个特征是相同的或者有关联的（Task02：基于统计学的方法 - 图55或者Task02：基于统计学的方法 - 图56）
解决方法：
对于1的情况，我们可以增加样本的数量；对于2的情况，我们应该找到相关的特征，去除多余的特征。

例子：
这里沿用2.2.1里面的设定，把独立多元高斯分布改成特征具有相关性的多元高斯分布。

from scipy.stats import multivariate_normal

mean_1, theta_1 = 5, 2
mean_2, theta_2 = 3, 1
X = np.arange(mean_1-4*theta_1, mean_1+4*theta_1, 0.2)
Y = np.arange(mean_2-4*theta_2, mean_2+4*theta_2, 0.2)
X, Y = np.meshgrid(X, Y)
data_model = np.concatenate([X.reshape((-1, 1)), Y.reshape((-1,1))], axis=1)
model = multivariate_normal.pdf(data_model, mean=[mean_1, mean_2], cov=[theta_1, theta_2])

plt.figure()
ContourSet = plt.contour(X, Y, model.reshape(X.shape), [0, 0.005, 0.1], linewidths=0) 
plt.setp(ContourSet.collections[1], lw=3, color='red', alpha=0.8)
manual_locations = [(ContourSet.levels[1], ContourSet.levels[-1])]

fmt = {}
strs = [None, '$\epsilon=0.005$', None]
for l, s in zip([0, 0.005, 0.1], strs):
    fmt[l] = s
plt.clabel(ContourSet, inline=1, fontsize=10, manual=manual_locations, fmt=fmt)
plt.text(mean_1, mean_2, "$p(x)>\epsilon$", fontsize=12, 
        bbox={'facecolor': 'c', 'alpha': 0.2, 'pad': 2} )
plt.text(5*theta_1, 5*theta_2, "$p(x)<\epsilon$", fontsize=12,
        bbox={'facecolor': 'r', 'alpha': 0.2, 'pad': 2} )

plt.scatter(data[0], data[1], marker='x')
plt.xlabel(r"$x_1$", size=15)
plt.ylabel(r"$x_2$", size=15)
plt.title("Anomaly Detection based on Multivariate Normal Distribution")
plt.show()

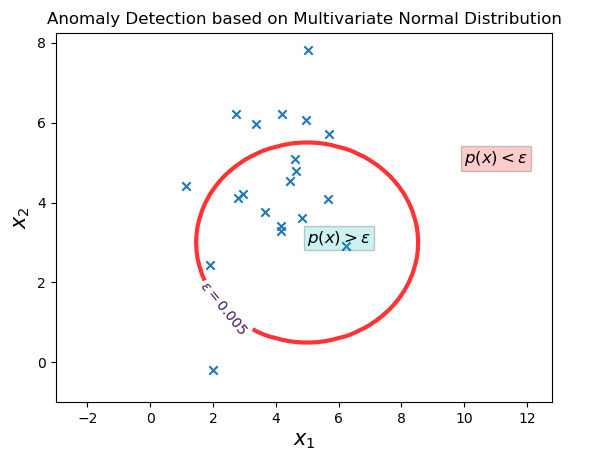
image.png

把独立多元高斯分布和特征相关多元高斯分布放到一起对比。可以看出同一份数据，特征相关多元高斯分布的“边界更接近正圆形”。
个人认为，这是因为特征支架具有相关性，导致2个特征发生的概率更接近，所以数据范围会更接近。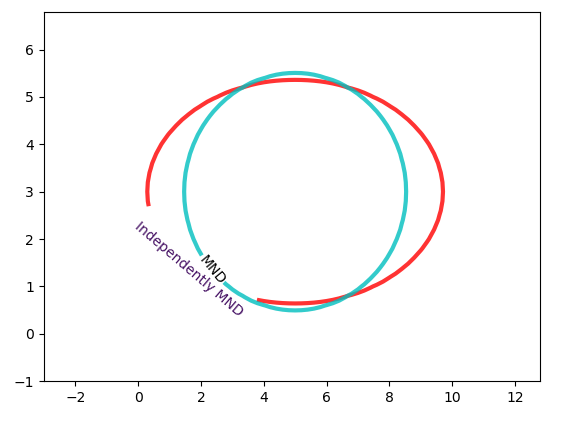
image.png

多元高斯模型的用法：

# mean_1, theta_1 = 5, 2
# mean_2, theta_2 = 3, 1
# data = multivariate_normal.rvs(mean=[mean_1, mean_2], cov=[theta_1, theta_2],
#                                size=(20), random_state=2021)

# 2.2.1中data的格式是(2,20)，在这里需要转置成（20,2)的格式。
P = multivariate_normal.pdf(data.T, mean=[mean_1, mean_2], cov=[theta_1, theta_2])
label_ = (P<0.005).astype(np.int8)  # 异常点的预测值为1，正常点的预测值为0
print('异常样本点：\n{}'.format(data[label_==1]))

异常样本点： [[ 5.01401631 3.37232295 5.69628739 4.96750275 4.18631027 2.74306981 1.13841641 1.99569105] [ 7.8173719 5.97593668 5.72085398 6.06439114 6.22766189 6.22364837 4.41834064 -0.19029586]]

参考资料：

  • 多元高斯分布完全解析：

https://zhuanlan.zhihu.com/p/58987388

  • 多元高斯分布（The Multivariate normal distribution）

https://www.cnblogs.com/bingjianing/p/9117330.html

2.2.3 使用混合参数分布

在许多情况下假定数据是由正态分布产生的。当实际数据很复杂时，这种假定过于简单，可以假定数据是被混合参数分布产生的。

比如高斯混合模型（Gaussian Mixture Model）：就是数据的分布可能不是单一的，可能是空间内的多个高斯分布，可以用EM算法来对模型进行最大似然估计，找到最佳分布。

高斯混合模型（GMM）推导及实现 ：https://zhuanlan.zhihu.com/p/85338773

3. 非参数方法

在异常检测的非参数方法中，“正常数据”的模型从输入数据学习，而不是假定一个先验。通常，非参数方法对数据做较少假定，因而在更多情况下都可以使用。

对总体的分布形态不清楚或总体分布不是正态分布，所以无法用参数检验来推断总体的集中趋势和离散程度的参数。统计学家想到用排秩（排序）的方法来规避不是正态分布的问题，用样本的排序情况来推断总体的分布情况。这就好比梁山一百单八将排好了座次，从中随机抽出几个，测试武力值，大概其能够了解梁山的实力如何。
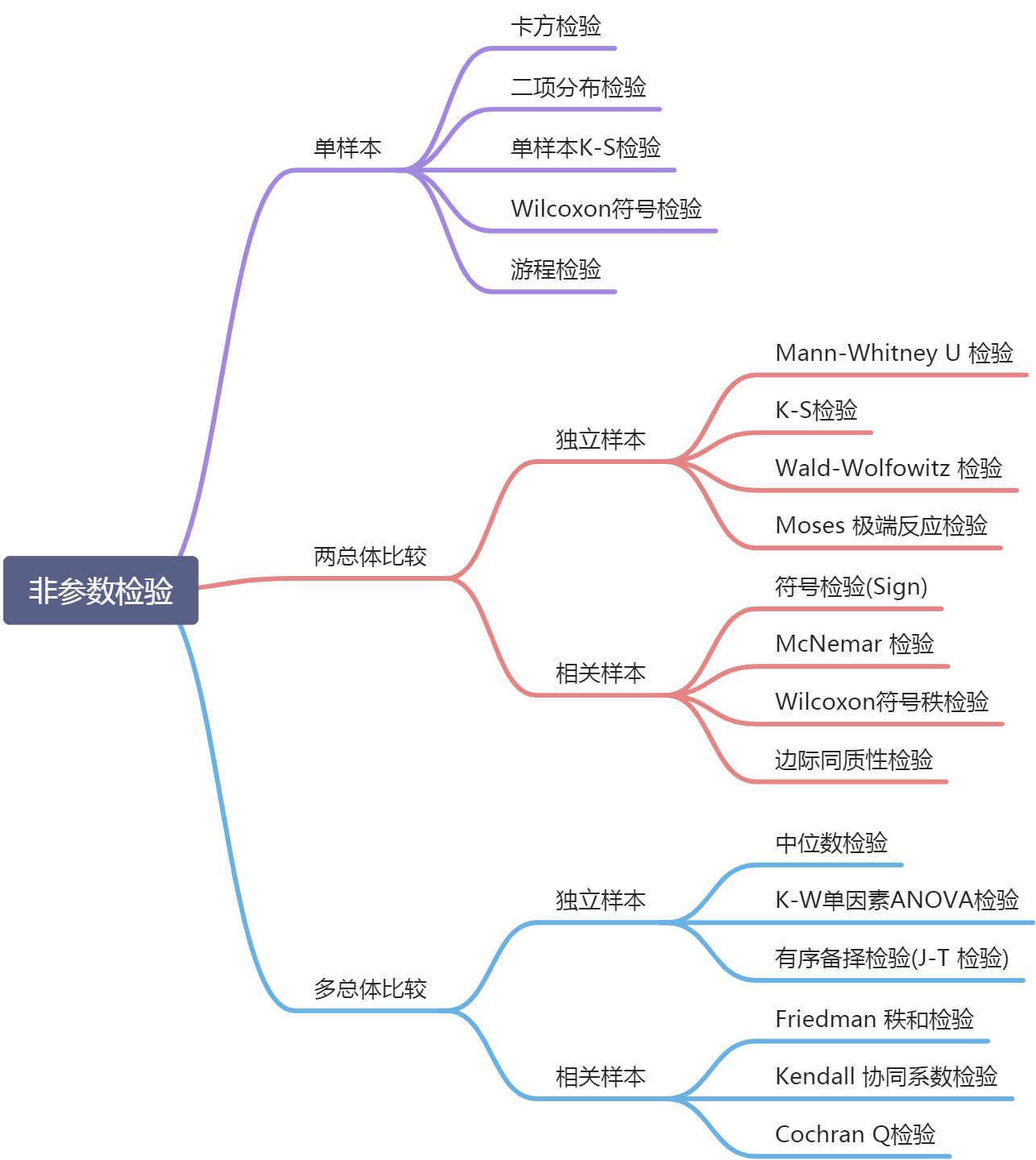
下图是非参数检验常用的检验方法表。接下来会具体介绍它们的检验理论和距离的案例应用。总体分布情况很多时候是未知或非正态分布的，所以非参数检验在现实生活中的应用很广泛。 Task02：基于统计学的方法 - 图59

如何理解非参数检验？ https://zhuanlan.zhihu.com/p/49472487


3.1 使用直方图检测异常点

直方图是一种频繁使用的非参数统计模型，可以用来检测异常点。该过程包括如下两步：

步骤1：构造直方图。使用输入数据（训练数据）构造一个直方图。该直方图可以是一元的，或者多元的（如果输入数据是多维的）。
尽管非参数方法并不假定任何先验统计模型，但是通常确实要求用户提供参数，以便由数据学习。例如，用户必须指定直方图的类型（等宽的或等深的）和其他参数（直方图中的箱数或每个箱的大小等）。与参数方法不同，这些参数并不指定数据分布的类型。

步骤2：检测异常点。为了确定一个对象是否是异常点，可以对照直方图检查它。在最简单的方法中，如果该对象落入直方图的一个箱中，则该对象被看作正常的，否则被认为是异常点。
对于更复杂的方法，可以使用直方图赋予每个对象一个异常点得分。例如令对象的异常点得分为该对象落入的箱的容积的倒数。

使用直方图作为异常点检测的非参数模型的一个缺点是，很难选择一个合适的箱尺寸。一方面，如果箱尺寸太小，则许多正常对象都会落入空的或稀疏的箱中，因而被误识别为异常点。另一方面，如果箱尺寸太大，则异常点对象可能渗入某些频繁的箱中，因而“假扮”成正常的。


3.2 基于频数直方图的无监督异常点检测算法——HBOS

HBOS全名为：Histogram-based Outlier Score。它是一种单变量方法的组合，不能对特征之间的依赖关系进行建模，但是计算速度较快，对大数据集友好。其基本假设是数据集的每个维度相互独立。然后对每个维度进行区间(bin)划分，区间的密度越高，异常评分越低。

HBOS算法流程：

1.为每个数据维度做出数据直方图。对分类数据统计每个值的频数并计算相对频率。对数值数据根据分布的不同采用以下两种方法：

1.静态宽度直方图：标准的直方图构建方法，在值范围内使用k个等宽箱。样本落入每个桶的频率（相对数量）作为密度（箱子高度）的估计。 时间复杂度：Task02：基于统计学的方法 - 图60#card=math&code=O%28n%29)

2.动态宽度直方图：首先对所有值进行排序，然后固定数量的Task02：基于统计学的方法 - 图61个连续值装进一个箱里，其中N是总实例数，k是箱个数；直方图中的箱面积表示实例数。因为箱的宽度是由箱中第一个值和最后一个值决定的，所有箱的面积都一样，因此每一个箱的高度都是可计算的。这意味着跨度大的箱的高度低，即密度小，只有一种情况例外，超过k个数相等，此时允许在同一个箱里超过Task02：基于统计学的方法 - 图62值。 时间复杂度：Task02：基于统计学的方法 - 图63)#card=math&code=O%28n%5Ctimes%20log%28n%29%29)

2.对每个维度都计算了一个独立的直方图，其中每个箱子的高度表示密度的估计。然后为了使得最大高度为1（确保了每个特征与异常值得分的权重相等），对直方图进行归一化处理。最后，每一个实例的HBOS值由以下公式计算：

Task02：基于统计学的方法 - 图64%3D%5Csum%7Bi%3D0%7D%5E%7Bd%7D%20%5Clog%20%5Cleft(%5Cfrac%7B1%7D%7B%5Ctext%20%7Bhist%7D%7Bi%7D(p)%7D%5Cright)%0A#card=math&code=H%20B%20O%20S%28p%29%3D%5Csum%7Bi%3D0%7D%5E%7Bd%7D%20%5Clog%20%5Cleft%28%5Cfrac%7B1%7D%7B%5Ctext%20%7Bhist%7D%7Bi%7D%28p%29%7D%5Cright%29%0A)

推导过程：

假设样本p第 i 个特征的概率密度为Task02：基于统计学的方法 - 图65#card=math&code=pi%28p%29) ，则_p的概率密度可以计算为：

Task02：基于统计学的方法 - 图66%3DP%7B1%7D(p)%20P%7B2%7D(p)%20%5Ccdots%20P%7Bd%7D(p)%0A#card=math&code=P%28p%29%3DP%7B1%7D%28p%29%20P%7B2%7D%28p%29%20%5Ccdots%20P%7Bd%7D%28p%29%0A)

两边取对数：

Task02：基于统计学的方法 - 图67)%20%26%3D%5Clog%20%5Cleft(P%7B1%7D(p)%20P%7B2%7D(p)%20%5Ccdots%20P%7Bd%7D(p)%5Cright)%20%3D%5Csum%7Bi%3D1%7D%5E%7Bd%7D%20%5Clog%20%5Cleft(P%7Bi%7D(p)%5Cright)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%5Clog%20%28P%28p%29%29%20%26%3D%5Clog%20%5Cleft%28P%7B1%7D%28p%29%20P%7B2%7D%28p%29%20%5Ccdots%20P%7Bd%7D%28p%29%5Cright%29%20%3D%5Csum%7Bi%3D1%7D%5E%7Bd%7D%20%5Clog%20%5Cleft%28P%7Bi%7D%28p%29%5Cright%29%0A%5Cend%7Baligned%7D%0A)

概率密度越大，异常评分越小，为了方便评分，两边乘以“-1”：

Task02：基于统计学的方法 - 图68)%3D-1%20%5Csum%7Bi%3D1%7D%5E%7Bd%7D%20%5Clog%20%5Cleft(P%7Bt%7D(p)%5Cright)%3D%5Csum%7Bi%3D1%7D%5E%7Bd%7D%20%5Cfrac%7B1%7D%7B%5Clog%20%5Cleft(P%7Bi%7D(p)%5Cright)%7D%0A#card=math&code=-%5Clog%20%28P%28p%29%29%3D-1%20%5Csum%7Bi%3D1%7D%5E%7Bd%7D%20%5Clog%20%5Cleft%28P%7Bt%7D%28p%29%5Cright%29%3D%5Csum%7Bi%3D1%7D%5E%7Bd%7D%20%5Cfrac%7B1%7D%7B%5Clog%20%5Cleft%28P%7Bi%7D%28p%29%5Cright%29%7D%0A)

最后可得：

Task02：基于统计学的方法 - 图69%3D-%5Clog%20(P(p))%3D%5Csum%7Bi%3D1%7D%5E%7Bd%7D%20%5Cfrac%7B1%7D%7B%5Clog%20%5Cleft(P%7Bi%7D(p)%5Cright)%7D%0A#card=math&code=H%20B%20O%20S%28p%29%3D-%5Clog%20%28P%28p%29%29%3D%5Csum%7Bi%3D1%7D%5E%7Bd%7D%20%5Cfrac%7B1%7D%7B%5Clog%20%5Cleft%28P%7Bi%7D%28p%29%5Cright%29%7D%0A)

练习：
使用PyOD库生成toy example并调用HBOS

from pyod.utils.data import generate_data
from pyod.models.hbos import HBOS
from pyod.utils.example import visualize
from pyod.utils.data import evaluate_print


contamination = 0.05  # 异常值的比例
n_train = 2000  # 训练集样本容量
n_test = 1000  # 测试样本容量

# 生成样本数据集
X_train, y_train, X_test, y_test =  generate_data(n_train=n_train, n_test=n_test,
                                                   n_features=2,  contamination=contamination,
                                                   random_state=42)
# 模型训练
model_name = 'HBOS'
model = HBOS()
model.fit(X_train)
y_train_pred = model.labels_  # 训练集训练后生成的标签，0为正常值，1为异常值
y_train_scores = model.decision_scores_   # 训练数据的异常值得分
params = model.get_params()  # 模型参数的估计量

# 对测试集进行预测
y_test_pred = model.predict(X_test)  # 生成测试集的预测标签
y_test_scores = model.decision_function(X_test)  # 使用合适的探测器预测X的原始异常分数。

# 打印评估结果
print("\nParams: ", params)
print("\nOn Training Data:")
evaluate_print(model_name, y_train, y_train_scores)
print("\nOn Test Data:")
evaluate_print(model_name, y_test, y_test_scores)

# 评估结果的可视化
visualize(model_name, X_train, y_train, X_test, y_test, y_train_pred,
              y_test_pred, show_figure=True, save_figure=True)

输出：

Params: {‘alpha’: 0.1, ‘contamination’: 0.1, ‘n_bins’: 10, ‘tol’: 0.5}

On Training Data: HBOS ROC:0.9948, precision @ rank n:0.9333

On Test Data:

HBOS ROC:0.9866, precision @ rank n:0.8542

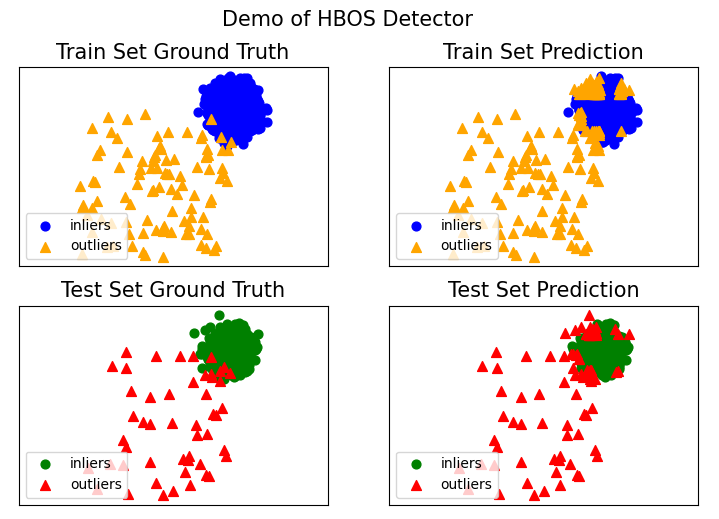
image.png

pyod.models.hbos.HBOS 的API文档

https://pyod.readthedocs.io/en/latest/pyod.models.html#module-pyod.models.hbos


4. 总结

1.异常检测的统计学方法由数据学习模型，以区别正常的数据对象和异常点。使用统计学方法的一个优点是，异常检测可以是统计上无可非议的。当然，仅当对数据所做的统计假定满足实际约束时才为真。

2.HBOS在全局异常检测问题上表现良好，但不能检测局部异常值。但是HBOS比标准算法快得多，尤其是在大数据集上。

3.统计学方法的优缺点

  • 优点：
    • 有坚实的统计学基础
    • 对单维数据，非常好用，是可以考虑的，对一些重要的维度，比如温度单独考察
  • 缺点：
    • 高维数据不太友好，性能比较差
    • 需要充分的数据和所用的检验类型的知识

更多参考资料：

[1]Goldstein, M. and Dengel, A., 2012. Histogram-based outlier score (hbos):A fast unsupervised anomaly detection algorithm . InKI-2012: Poster and Demo Track, pp.59-63.

[2]http://speech.ee.ntu.edu.tw/~tlkagk/courses.html

[3]http://cs229.stanford.edu/

**