1. 前向分步算法
回看Adaboost的算法内容,我们需要通过计算M个基本分类器,每个分类器的错误率、样本权重以及模型权重。我们可以认为:Adaboost每次学习单一分类器以及单一分类器的参数(权重)。接下来,我们抽象出Adaboost算法的整体框架逻辑,构建集成学习的一个非常重要的框架——前向分步算法,有了这个框架,我们不仅可以解决分类问题,也可以解决回归问题。
1.1 加法模型
在Adaboost模型中,我们把每个基本分类器合成一个复杂分类器的方法是每个基本分类器的加权和,即:%3D%5Csum%7Bm%3D1%7D%5E%7BM%7D%20%5Cbeta%7Bm%7D%20b%5Cleft(x%20%3B%20%5Cgamma%7Bm%7D%5Cright)#card=math&code=f%28x%29%3D%5Csum%7Bm%3D1%7D%5E%7BM%7D%20%5Cbeta%7Bm%7D%20b%5Cleft%28x%20%3B%20%5Cgamma%7Bm%7D%5Cright%29&id=wX28V),其中,
#card=math&code=b%5Cleft%28x%20%3B%20%5Cgamma%7Bm%7D%5Cright%29&id=GNkdK)为即基本分类器,为基本分类器的参数,
为基本分类器的权重,显然这与第二章所学的加法模型。为什么这么说呢?大家把#card=math&code=b%28x%20%3B%20%5Cgamma_%7Bm%7D%29&id=XMCNu)看成是即函数即可。
在给定训练数据以及损失函数)#card=math&code=L%28y%2C%20f%28x%29%29&id=mrygY)的条件下,学习加法模型
#card=math&code=f%28x%29&id=C39Ob)就是:
%5Cright)%0A#card=math&code=%5Cmin%20%7B%5Cbeta%7Bm%7D%2C%20%5Cgamma%7Bm%7D%7D%20%5Csum%7Bi%3D1%7D%5E%7BN%7D%20L%5Cleft%28y%7Bi%7D%2C%20%5Csum%7Bm%3D1%7D%5E%7BM%7D%20%5Cbeta%7Bm%7D%20b%5Cleft%28x%7Bi%7D%20%3B%20%5Cgamma_%7Bm%7D%5Cright%29%5Cright%29%0A&id=HB7Ba)
通常这是一个复杂的优化问题,很难通过简单的凸优化的相关知识进行解决。前向分步算法可以用来求解这种方式的问题,它的基本思路是:因为学习的是加法模型,如果从前向后,每一步只优化一个基函数及其系数,逐步逼近目标函数,那么就可以降低优化的复杂度。具体而言,每一步只需要优化:
%5Cright)%0A#card=math&code=%5Cmin%20%7B%5Cbeta%2C%20%5Cgamma%7D%20%5Csum%7Bi%3D1%7D%5E%7BN%7D%20L%5Cleft%28y%7Bi%7D%2C%20%5Cbeta%20b%5Cleft%28x%7Bi%7D%20%3B%20%5Cgamma%5Cright%29%5Cright%29%0A&id=JWgEy)
1.2 前向分步算法
给定数据集%2C%5Cleft(x%7B2%7D%2C%20y%7B2%7D%5Cright)%2C%20%5Ccdots%2C%5Cleft(x%7BN%7D%2C%20y%7BN%7D%5Cright)%5Cright%5C%7D#card=math&code=T%3D%5Cleft%5C%7B%5Cleft%28x%7B1%7D%2C%20y%7B1%7D%5Cright%29%2C%5Cleft%28x%7B2%7D%2C%20y%7B2%7D%5Cright%29%2C%20%5Ccdots%2C%5Cleft%28x%7BN%7D%2C%20y%7BN%7D%5Cright%29%5Cright%5C%7D&id=Z1qNi),
,
。损失函数
)#card=math&code=L%28y%2C%20f%28x%29%29&id=pMxRy),基函数集合
%5C%7D#card=math&code=%5C%7Bb%28x%20%3B%20%5Cgamma%29%5C%7D&id=ZuWwO),我们需要输出加法模型
#card=math&code=f%28x%29&id=gsklq)。
- 初始化:
%3D0#card=math&code=f_%7B0%7D%28x%29%3D0&id=eKaLe)
- 对m = 1,2,…,M:
- (a) 极小化损失函数:
%3D%5Carg%20%5Cmin%20%7B%5Cbeta%2C%20%5Cgamma%7D%20%5Csum%7Bi%3D1%7D%5E%7BN%7D%20L%5Cleft(y%7Bi%7D%2C%20f%7Bm-1%7D%5Cleft(x%7Bi%7D%5Cright)%2B%5Cbeta%20b%5Cleft(x%7Bi%7D%20%3B%20%5Cgamma%5Cright)%5Cright)%0A#card=math&code=%5Cleft%28%5Cbeta%7Bm%7D%2C%20%5Cgamma%7Bm%7D%5Cright%29%3D%5Carg%20%5Cmin%20%7B%5Cbeta%2C%20%5Cgamma%7D%20%5Csum%7Bi%3D1%7D%5E%7BN%7D%20L%5Cleft%28y%7Bi%7D%2C%20f%7Bm-1%7D%5Cleft%28x%7Bi%7D%5Cright%29%2B%5Cbeta%20b%5Cleft%28x%7Bi%7D%20%3B%20%5Cgamma%5Cright%29%5Cright%29%0A&id=WWDWm)
得到参数与
- (b) 更新:
%3Df%7Bm-1%7D(x)%2B%5Cbeta%7Bm%7D%20b%5Cleft(x%20%3B%20%5Cgamma%7Bm%7D%5Cright)%0A#card=math&code=f%7Bm%7D%28x%29%3Df%7Bm-1%7D%28x%29%2B%5Cbeta%7Bm%7D%20b%5Cleft%28x%20%3B%20%5Cgamma_%7Bm%7D%5Cright%29%0A&id=fOMnp)
- 得到加法模型:
%3Df%7BM%7D(x)%3D%5Csum%7Bm%3D1%7D%5E%7BM%7D%20%5Cbeta%7Bm%7D%20b%5Cleft(x%20%3B%20%5Cgamma%7Bm%7D%5Cright)%0A#card=math&code=f%28x%29%3Df%7BM%7D%28x%29%3D%5Csum%7Bm%3D1%7D%5E%7BM%7D%20%5Cbeta%7Bm%7D%20b%5Cleft%28x%20%3B%20%5Cgamma%7Bm%7D%5Cright%29%0A&id=FiIQl)
这样,前向分步算法将同时求解从m=1到M的所有参数,
的优化问题简化为逐次求解各个
,
的问题。
1.3 前向分步算法与Adaboost的关系
由于这里不是我们的重点,我们主要阐述这里的结论,不做相关证明,具体的证明见李航老师的《统计学习方法》第八章的3.2节。Adaboost算法是前向分步算法的特例,Adaboost算法是由基本分类器组成的加法模型,损失函数为指数损失函数。
2. 梯度提升决策树(GBDT)
2.1 基于残差学习的提升树算法
在前面的学习过程中,我们一直讨论的都是分类树,比如Adaboost算法,并没有涉及回归的例子。在上一小节我们提到了一个加法模型+前向分步算法的框架,那能否使用这个框架解决回归的例子呢?答案是肯定的。接下来我们来探讨下如何使用加法模型+前向分步算法的框架实现回归问题。
在使用加法模型+前向分步算法的框架解决问题之前,我们需要首先确定框架内使用的基函数是什么,在这里我们使用决策树分类器。前面第二章我们已经学过了回归树的基本原理,树算法最重要是寻找最佳的划分点,分类树用纯度来判断最佳划分点使用信息增益(ID3算法),信息增益比(C4.5算法),基尼系数(CART分类树)。但是在回归树中的样本标签是连续数值,可划分点包含了所有特征的所有可取的值。所以再使用熵之类的指标不再合适,取而代之的是平方误差,它能很好的评判拟合程度。基函数确定了以后,我们需要确定每次提升的标准是什么。回想Adaboost算法,在Adaboost算法内使用了分类错误率修正样本权重以及计算每个基本分类器的权重,那回归问题没有分类错误率可言,也就没办法在这里的回归问题使用了,因此我们需要另辟蹊径。模仿分类错误率,我们用每个样本的残差表示每次使用基函数预测时没有解决的那部分问题。因此,我们可以得出如下算法:
输入数据集%2C%5Cleft(x%7B2%7D%2C%20y%7B2%7D%5Cright)%2C%20%5Ccdots%2C%5Cleft(x%7BN%7D%2C%20y%7BN%7D%5Cright)%5Cright%5C%7D%2C%20x%7Bi%7D%20%5Cin%20%5Cmathcal%7BX%7D%20%5Csubseteq%20%5Cmathbf%7BR%7D%5E%7Bn%7D%2C%20y%7Bi%7D%20%5Cin%20%5Cmathcal%7BY%7D%20%5Csubseteq%20%5Cmathbf%7BR%7D#card=math&code=T%3D%5Cleft%5C%7B%5Cleft%28x%7B1%7D%2C%20y%7B1%7D%5Cright%29%2C%5Cleft%28x%7B2%7D%2C%20y%7B2%7D%5Cright%29%2C%20%5Ccdots%2C%5Cleft%28x%7BN%7D%2C%20y%7BN%7D%5Cright%29%5Cright%5C%7D%2C%20x%7Bi%7D%20%5Cin%20%5Cmathcal%7BX%7D%20%5Csubseteq%20%5Cmathbf%7BR%7D%5E%7Bn%7D%2C%20y%7Bi%7D%20%5Cin%20%5Cmathcal%7BY%7D%20%5Csubseteq%20%5Cmathbf%7BR%7D&id=APw3G),输出最终的提升树
#card=math&code=f_%7BM%7D%28x%29&id=eS65D)
- 初始化
%20%3D%200#card=math&code=f_0%28x%29%20%3D%200&id=NEEHC)
- 对m = 1,2,…,M:
- 计算每个样本的残差:
%2C%20%5Cquad%20i%3D1%2C2%2C%20%5Ccdots%2C%20N#card=math&code=r%7Bm%20i%7D%3Dy%7Bi%7D-f%7Bm-1%7D%5Cleft%28x%7Bi%7D%5Cright%29%2C%20%5Cquad%20i%3D1%2C2%2C%20%5Ccdots%2C%20N&id=E006G)
- 拟合残差
学习一棵回归树,得到
#card=math&code=T%5Cleft%28x%20%3B%20%5CTheta_%7Bm%7D%5Cright%29&id=AUjxp)
- 更新
%3Df%7Bm-1%7D(x)%2BT%5Cleft(x%20%3B%20%5CTheta%7Bm%7D%5Cright)#card=math&code=f%7Bm%7D%28x%29%3Df%7Bm-1%7D%28x%29%2BT%5Cleft%28x%20%3B%20%5CTheta_%7Bm%7D%5Cright%29&id=CPMOQ)
- 计算每个样本的残差:
- 得到最终的回归问题的提升树:
%3D%5Csum%7Bm%3D1%7D%5E%7BM%7D%20T%5Cleft(x%20%3B%20%5CTheta%7Bm%7D%5Cright)#card=math&code=f%7BM%7D%28x%29%3D%5Csum%7Bm%3D1%7D%5E%7BM%7D%20T%5Cleft%28x%20%3B%20%5CTheta_%7Bm%7D%5Cright%29&id=HjFWW)
下面我们用一个实际的案例来使用这个算法:(案例来源:李航老师《统计学习方法》)
训练数据如下表,学习这个回归问题的提升树模型,考虑只用树桩作为基函数。




至此,我们已经能够建立起依靠加法模型+前向分步算法的框架解决回归问题的算法,叫提升树算法。那么,这个算法还是否有提升的空间呢?
2.2 梯度提升决策树算法(GBDT)
提升树利用加法模型和前向分步算法实现学习的过程,当损失函数为平方损失和指数损失时,每一步优化是相当简单的,也就是我们前面探讨的提升树算法和Adaboost算法。但是对于一般的损失函数而言,往往每一步的优化不是那么容易,针对这一问题,我们得分析问题的本质,也就是是什么导致了在一般损失函数条件下的学习困难。对比以下损失函数:
%5Cright)%20%2F%20%5Cpartial%20f%5Cleft(x%7Bi%7D%5Cright)%20%5C%5C%0A%5Chline%20%5Ctext%20%7B%20Regression%20%7D%20%26%20%5Cfrac%7B1%7D%7B2%7D%5Cleft%5By%7Bi%7D-f%5Cleft(x%7Bi%7D%5Cright)%5Cright%5D%5E%7B2%7D%20%26%20y%7Bi%7D-f%5Cleft(x%7Bi%7D%5Cright)%20%5C%5C%0A%5Chline%20%5Ctext%20%7B%20Regression%20%7D%20%26%20%5Cleft%7Cy%7Bi%7D-f%5Cleft(x%7Bi%7D%5Cright)%5Cright%7C%20%26%20%5Coperatorname%7Bsign%7D%5Cleft%5By%7Bi%7D-f%5Cleft(x%7Bi%7D%5Cright)%5Cright%5D%20%5C%5C%0A%5Chline%20%5Ctext%20%7B%20Regression%20%7D%20%26%20%5Ctext%20%7B%20Huber%20%7D%20%26%20y%7Bi%7D-f%5Cleft(x%7Bi%7D%5Cright)%20%5Ctext%20%7B%20for%20%7D%5Cleft%7Cy%7Bi%7D-f%5Cleft(x%7Bi%7D%5Cright)%5Cright%7C%20%5Cleq%20%5Cdelta%7Bm%7D%20%5C%5C%0A%26%20%26%20%5Cdelta%7Bm%7D%20%5Coperatorname%7Bsign%7D%5Cleft%5By%7Bi%7D-f%5Cleft(x%7Bi%7D%5Cright)%5Cright%5D%20%5Ctext%20%7B%20for%20%7D%5Cleft%7Cy%7Bi%7D-f%5Cleft(x%7Bi%7D%5Cright)%5Cright%7C%3E%5Cdelta%7Bm%7D%20%5C%5C%0A%26%20%26%20%5Ctext%20%7B%20where%20%7D%20%5Cdelta%7Bm%7D%3D%5Calpha%20%5Ctext%20%7B%20th-quantile%20%7D%5Cleft%5C%7B%5Cleft%7Cy%7Bi%7D-f%5Cleft(x%7Bi%7D%5Cright)%5Cright%7C%5Cright%5C%7D%20%5C%5C%0A%5Chline%20%5Ctext%20%7B%20Classification%20%7D%20%26%20%5Ctext%20%7B%20Deviance%20%7D%20%26%20k%20%5Ctext%20%7B%20th%20component%3A%20%7D%20I%5Cleft(y%7Bi%7D%3D%5Cmathcal%7BG%7D%7Bk%7D%5Cright)-p%7Bk%7D%5Cleft(x%7Bi%7D%5Cright)%20%5C%5C%0A%5Chline%0A%5Cend%7Barray%7D%0A#card=math&code=%5Cbegin%7Barray%7D%7Bl%7Cl%7Cl%7D%0A%5Chline%20%5Ctext%20%7B%20Setting%20%7D%20%26%20%5Ctext%20%7B%20Loss%20Function%20%7D%20%26%20-%5Cpartial%20L%5Cleft%28y%7Bi%7D%2C%20f%5Cleft%28x%7Bi%7D%5Cright%29%5Cright%29%20%2F%20%5Cpartial%20f%5Cleft%28x%7Bi%7D%5Cright%29%20%5C%5C%0A%5Chline%20%5Ctext%20%7B%20Regression%20%7D%20%26%20%5Cfrac%7B1%7D%7B2%7D%5Cleft%5By%7Bi%7D-f%5Cleft%28x%7Bi%7D%5Cright%29%5Cright%5D%5E%7B2%7D%20%26%20y%7Bi%7D-f%5Cleft%28x%7Bi%7D%5Cright%29%20%5C%5C%0A%5Chline%20%5Ctext%20%7B%20Regression%20%7D%20%26%20%5Cleft%7Cy%7Bi%7D-f%5Cleft%28x%7Bi%7D%5Cright%29%5Cright%7C%20%26%20%5Coperatorname%7Bsign%7D%5Cleft%5By%7Bi%7D-f%5Cleft%28x%7Bi%7D%5Cright%29%5Cright%5D%20%5C%5C%0A%5Chline%20%5Ctext%20%7B%20Regression%20%7D%20%26%20%5Ctext%20%7B%20Huber%20%7D%20%26%20y%7Bi%7D-f%5Cleft%28x%7Bi%7D%5Cright%29%20%5Ctext%20%7B%20for%20%7D%5Cleft%7Cy%7Bi%7D-f%5Cleft%28x%7Bi%7D%5Cright%29%5Cright%7C%20%5Cleq%20%5Cdelta%7Bm%7D%20%5C%5C%0A%26%20%26%20%5Cdelta%7Bm%7D%20%5Coperatorname%7Bsign%7D%5Cleft%5By%7Bi%7D-f%5Cleft%28x%7Bi%7D%5Cright%29%5Cright%5D%20%5Ctext%20%7B%20for%20%7D%5Cleft%7Cy%7Bi%7D-f%5Cleft%28x%7Bi%7D%5Cright%29%5Cright%7C%3E%5Cdelta%7Bm%7D%20%5C%5C%0A%26%20%26%20%5Ctext%20%7B%20where%20%7D%20%5Cdelta%7Bm%7D%3D%5Calpha%20%5Ctext%20%7B%20th-quantile%20%7D%5Cleft%5C%7B%5Cleft%7Cy%7Bi%7D-f%5Cleft%28x%7Bi%7D%5Cright%29%5Cright%7C%5Cright%5C%7D%20%5C%5C%0A%5Chline%20%5Ctext%20%7B%20Classification%20%7D%20%26%20%5Ctext%20%7B%20Deviance%20%7D%20%26%20k%20%5Ctext%20%7B%20th%20component%3A%20%7D%20I%5Cleft%28y%7Bi%7D%3D%5Cmathcal%7BG%7D%7Bk%7D%5Cright%29-p%7Bk%7D%5Cleft%28x%7Bi%7D%5Cright%29%20%5C%5C%0A%5Chline%0A%5Cend%7Barray%7D%0A&id=D7dVS)
观察Huber损失函数:
)%3D%5Cleft%5C%7B%5Cbegin%7Barray%7D%7Bll%7D%0A%5Cfrac%7B1%7D%7B2%7D(y-f(x))%5E%7B2%7D%20%26%20%5Ctext%20%7B%20for%20%7D%7Cy-f(x)%7C%20%5Cleq%20%5Cdelta%20%5C%5C%0A%5Cdelta%7Cy-f(x)%7C-%5Cfrac%7B1%7D%7B2%7D%20%5Cdelta%5E%7B2%7D%20%26%20%5Ctext%20%7B%20otherwise%20%7D%0A%5Cend%7Barray%7D%5Cright.%0A#card=math&code=L_%7B%5Cdelta%7D%28y%2C%20f%28x%29%29%3D%5Cleft%5C%7B%5Cbegin%7Barray%7D%7Bll%7D%0A%5Cfrac%7B1%7D%7B2%7D%28y-f%28x%29%29%5E%7B2%7D%20%26%20%5Ctext%20%7B%20for%20%7D%7Cy-f%28x%29%7C%20%5Cleq%20%5Cdelta%20%5C%5C%0A%5Cdelta%7Cy-f%28x%29%7C-%5Cfrac%7B1%7D%7B2%7D%20%5Cdelta%5E%7B2%7D%20%26%20%5Ctext%20%7B%20otherwise%20%7D%0A%5Cend%7Barray%7D%5Cright.%0A&id=PhNaY)
针对上面的问题,Freidman提出了梯度提升算法(gradient boosting),这是利用最速下降法的近似方法,利用损失函数的负梯度在当前模型的值%5Cright)%7D%7B%5Cpartial%20f%5Cleft(x%7Bi%7D%5Cright)%7D%5Cright%5D%7Bf(x)%3Df%7Bm-1%7D(x)%7D#card=math&code=-%5Cleft%5B%5Cfrac%7B%5Cpartial%20L%5Cleft%28y%2C%20f%5Cleft%28x%7Bi%7D%5Cright%29%5Cright%29%7D%7B%5Cpartial%20f%5Cleft%28x%7Bi%7D%5Cright%29%7D%5Cright%5D%7Bf%28x%29%3Df_%7Bm-1%7D%28x%29%7D&id=UCcV7)作为回归问题提升树算法中的残差的近似值,拟合回归树。与其说负梯度作为残差的近似值,不如说残差是负梯度的一种特例。
2.2.1 梯度提升法的算法流程
以下开始具体介绍梯度提升算法:
输入训练数据集%2C%5Cleft(x%7B2%7D%2C%20y%7B2%7D%5Cright)%2C%20%5Ccdots%2C%5Cleft(x%7BN%7D%2C%20y%7BN%7D%5Cright)%5Cright%5C%7D%2C%20x%7Bi%7D%20%5Cin%20%5Cmathcal%7BX%7D%20%5Csubseteq%20%5Cmathbf%7BR%7D%5E%7Bn%7D%2C%20y%7Bi%7D%20%5Cin%20%5Cmathcal%7BY%7D%20%5Csubseteq%20%5Cmathbf%7BR%7D#card=math&code=T%3D%5Cleft%5C%7B%5Cleft%28x%7B1%7D%2C%20y%7B1%7D%5Cright%29%2C%5Cleft%28x%7B2%7D%2C%20y%7B2%7D%5Cright%29%2C%20%5Ccdots%2C%5Cleft%28x%7BN%7D%2C%20y%7BN%7D%5Cright%29%5Cright%5C%7D%2C%20x%7Bi%7D%20%5Cin%20%5Cmathcal%7BX%7D%20%5Csubseteq%20%5Cmathbf%7BR%7D%5E%7Bn%7D%2C%20y%7Bi%7D%20%5Cin%20%5Cmathcal%7BY%7D%20%5Csubseteq%20%5Cmathbf%7BR%7D&id=Y6uUu)和损失函数
)#card=math&code=L%28y%2C%20f%28x%29%29&id=WDxnr),输出回归树
#card=math&code=%5Chat%7Bf%7D%28x%29&id=zOaCp)
- 初始化
%3D%5Carg%20%5Cmin%20%7Bc%7D%20%5Csum%7Bi%3D1%7D%5E%7BN%7D%20L%5Cleft(y%7Bi%7D%2C%20c%5Cright)#card=math&code=f%7B0%7D%28x%29%3D%5Carg%20%5Cmin%20%7Bc%7D%20%5Csum%7Bi%3D1%7D%5E%7BN%7D%20L%5Cleft%28y_%7Bi%7D%2C%20c%5Cright%29&id=PPKhN)
对于m=1,2,…,M:
- 对每个样本i = 1,2,…,N计算负梯度,即残差:
%5Cright)%7D%7B%5Cpartial%20f%5Cleft(x%7Bi%7D%5Cright)%7D%5Cright%5D%7Bf(x)%3Df%7Bm-1%7D(x)%7D%3C%2Ftitle%3E%0A%3Cdefs%20aria-hidden%3D%22true%22%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-72%22%20d%3D%22M21%20287Q22%20290%2023%20295T28%20317T38%20348T53%20381T73%20411T99%20433T132%20442Q161%20442%20183%20430T214%20408T225%20388Q227%20382%20228%20382T236%20389Q284%20441%20347%20441H350Q398%20441%20422%20400Q430%20381%20430%20363Q430%20333%20417%20315T391%20292T366%20288Q346%20288%20334%20299T322%20328Q322%20376%20378%20392Q356%20405%20342%20405Q286%20405%20239%20331Q229%20315%20224%20298T190%20165Q156%2025%20151%2016Q138%20-11%20108%20-11Q95%20-11%2087%20-5T76%207T74%2017Q74%2030%20114%20189T154%20366Q154%20405%20128%20405Q107%20405%2092%20377T68%20316T57%20280Q55%20278%2041%20278H27Q21%20284%2021%20287Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-6D%22%20d%3D%22M21%20287Q22%20293%2024%20303T36%20341T56%20388T88%20425T132%20442T175%20435T205%20417T221%20395T229%20376L231%20369Q231%20367%20232%20367L243%20378Q303%20442%20384%20442Q401%20442%20415%20440T441%20433T460%20423T475%20411T485%20398T493%20385T497%20373T500%20364T502%20357L510%20367Q573%20442%20659%20442Q713%20442%20746%20415T780%20336Q780%20285%20742%20178T704%2050Q705%2036%20709%2031T724%2026Q752%2026%20776%2056T815%20138Q818%20149%20821%20151T837%20153Q857%20153%20857%20145Q857%20144%20853%20130Q845%20101%20831%2073T785%2017T716%20-10Q669%20-10%20648%2017T627%2073Q627%2092%20663%20193T700%20345Q700%20404%20656%20404H651Q565%20404%20506%20303L499%20291L466%20157Q433%2026%20428%2016Q415%20-11%20385%20-11Q372%20-11%20364%20-4T353%208T350%2018Q350%2029%20384%20161L420%20307Q423%20322%20423%20345Q423%20404%20379%20404H374Q288%20404%20229%20303L222%20291L189%20157Q156%2026%20151%2016Q138%20-11%20108%20-11Q95%20-11%2087%20-5T76%207T74%2017Q74%2030%20112%20181Q151%20335%20151%20342Q154%20357%20154%20369Q154%20405%20129%20405Q107%20405%2092%20377T69%20316T57%20280Q55%20278%2041%20278H27Q21%20284%2021%20287Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-69%22%20d%3D%22M184%20600Q184%20624%20203%20642T247%20661Q265%20661%20277%20649T290%20619Q290%20596%20270%20577T226%20557Q211%20557%20198%20567T184%20600ZM21%20287Q21%20295%2030%20318T54%20369T98%20420T158%20442Q197%20442%20223%20419T250%20357Q250%20340%20236%20301T196%20196T154%2083Q149%2061%20149%2051Q149%2026%20166%2026Q175%2026%20185%2029T208%2043T235%2078T260%20137Q263%20149%20265%20151T282%20153Q302%20153%20302%20143Q302%20135%20293%20112T268%2061T223%2011T161%20-11Q129%20-11%20102%2010T74%2074Q74%2091%2079%20106T122%20220Q160%20321%20166%20341T173%20380Q173%20404%20156%20404H154Q124%20404%2099%20371T61%20287Q60%20286%2059%20284T58%20281T56%20279T53%20278T49%20278T41%20278H27Q21%20284%2021%20287Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-3D%22%20d%3D%22M56%20347Q56%20360%2070%20367H707Q722%20359%20722%20347Q722%20336%20708%20328L390%20327H72Q56%20332%2056%20347ZM56%20153Q56%20168%2072%20173H708Q722%20163%20722%20153Q722%20140%20707%20133H70Q56%20140%2056%20153Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-2212%22%20d%3D%22M84%20237T84%20250T98%20270H679Q694%20262%20694%20250T679%20230H98Q84%20237%2084%20250Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-5B%22%20d%3D%22M118%20-250V750H255V710H158V-210H255V-250H118Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-2202%22%20d%3D%22M202%20508Q179%20508%20169%20520T158%20547Q158%20557%20164%20577T185%20624T230%20675T301%20710L333%20715H345Q378%20715%20384%20714Q447%20703%20489%20661T549%20568T566%20457Q566%20362%20519%20240T402%2053Q321%20-22%20223%20-22Q123%20-22%2073%2056Q42%20102%2042%20148V159Q42%20276%20129%20370T322%20465Q383%20465%20414%20434T455%20367L458%20378Q478%20461%20478%20515Q478%20603%20437%20639T344%20676Q266%20676%20223%20612Q264%20606%20264%20572Q264%20547%20246%20528T202%20508ZM430%20306Q430%20372%20401%20400T333%20428Q270%20428%20222%20382Q197%20354%20183%20323T150%20221Q132%20149%20132%20116Q132%2021%20232%2021Q244%2021%20250%2022Q327%2035%20374%20112Q389%20137%20409%20196T430%20306Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-4C%22%20d%3D%22M228%20637Q194%20637%20192%20641Q191%20643%20191%20649Q191%20673%20202%20682Q204%20683%20217%20683Q271%20680%20344%20680Q485%20680%20506%20683H518Q524%20677%20524%20674T522%20656Q517%20641%20513%20637H475Q406%20636%20394%20628Q387%20624%20380%20600T313%20336Q297%20271%20279%20198T252%2088L243%2052Q243%2048%20252%2048T311%2046H328Q360%2046%20379%2047T428%2054T478%2072T522%20106T564%20161Q580%20191%20594%20228T611%20270Q616%20273%20628%20273H641Q647%20264%20647%20262T627%20203T583%2083T557%209Q555%204%20553%203T537%200T494%20-1Q483%20-1%20418%20-1T294%200H116Q32%200%2032%2010Q32%2017%2034%2024Q39%2043%2044%2045Q48%2046%2059%2046H65Q92%2046%20125%2049Q139%2052%20144%2061Q147%2065%20216%20339T285%20628Q285%20635%20228%20637Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-28%22%20d%3D%22M94%20250Q94%20319%20104%20381T127%20488T164%20576T202%20643T244%20695T277%20729T302%20750H315H319Q333%20750%20333%20741Q333%20738%20316%20720T275%20667T226%20581T184%20443T167%20250T184%2058T225%20-81T274%20-167T316%20-220T333%20-241Q333%20-250%20318%20-250H315H302L274%20-226Q180%20-141%20137%20-14T94%20250Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-79%22%20d%3D%22M21%20287Q21%20301%2036%20335T84%20406T158%20442Q199%20442%20224%20419T250%20355Q248%20336%20247%20334Q247%20331%20231%20288T198%20191T182%20105Q182%2062%20196%2045T238%2027Q261%2027%20281%2038T312%2061T339%2094Q339%2095%20344%20114T358%20173T377%20247Q415%20397%20419%20404Q432%20431%20462%20431Q475%20431%20483%20424T494%20412T496%20403Q496%20390%20447%20193T391%20-23Q363%20-106%20294%20-155T156%20-205Q111%20-205%2077%20-183T43%20-117Q43%20-95%2050%20-80T69%20-58T89%20-48T106%20-45Q150%20-45%20150%20-87Q150%20-107%20138%20-122T115%20-142T102%20-147L99%20-148Q101%20-153%20118%20-160T152%20-167H160Q177%20-167%20186%20-165Q219%20-156%20247%20-127T290%20-65T313%20-9T321%2021L315%2017Q309%2013%20296%206T270%20-6Q250%20-11%20231%20-11Q185%20-11%20150%2011T104%2082Q103%2089%20103%20113Q103%20170%20138%20262T173%20379Q173%20380%20173%20381Q173%20390%20173%20393T169%20400T158%20404H154Q131%20404%20112%20385T82%20344T65%20302T57%20280Q55%20278%2041%20278H27Q21%20284%2021%20287Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-2C%22%20d%3D%22M78%2035T78%2060T94%20103T137%20121Q165%20121%20187%2096T210%208Q210%20-27%20201%20-60T180%20-117T154%20-158T130%20-185T117%20-194Q113%20-194%20104%20-185T95%20-172Q95%20-168%20106%20-156T131%20-126T157%20-76T173%20-3V9L172%208Q170%207%20167%206T161%203T152%201T140%200Q113%200%2096%2017Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-66%22%20d%3D%22M118%20-162Q120%20-162%20124%20-164T135%20-167T147%20-168Q160%20-168%20171%20-155T187%20-126Q197%20-99%20221%2027T267%20267T289%20382V385H242Q195%20385%20192%20387Q188%20390%20188%20397L195%20425Q197%20430%20203%20430T250%20431Q298%20431%20298%20432Q298%20434%20307%20482T319%20540Q356%20705%20465%20705Q502%20703%20526%20683T550%20630Q550%20594%20529%20578T487%20561Q443%20561%20443%20603Q443%20622%20454%20636T478%20657L487%20662Q471%20668%20457%20668Q445%20668%20434%20658T419%20630Q412%20601%20403%20552T387%20469T380%20433Q380%20431%20435%20431Q480%20431%20487%20430T498%20424Q499%20420%20496%20407T491%20391Q489%20386%20482%20386T428%20385H372L349%20263Q301%2015%20282%20-47Q255%20-132%20212%20-173Q175%20-205%20139%20-205Q107%20-205%2081%20-186T55%20-132Q55%20-95%2076%20-78T118%20-61Q162%20-61%20162%20-103Q162%20-122%20151%20-136T127%20-157L118%20-162Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-78%22%20d%3D%22M52%20289Q59%20331%20106%20386T222%20442Q257%20442%20286%20424T329%20379Q371%20442%20430%20442Q467%20442%20494%20420T522%20361Q522%20332%20508%20314T481%20292T458%20288Q439%20288%20427%20299T415%20328Q415%20374%20465%20391Q454%20404%20425%20404Q412%20404%20406%20402Q368%20386%20350%20336Q290%20115%20290%2078Q290%2050%20306%2038T341%2026Q378%2026%20414%2059T463%20140Q466%20150%20469%20151T485%20153H489Q504%20153%20504%20145Q504%20144%20502%20134Q486%2077%20440%2033T333%20-11Q263%20-11%20227%2052Q186%20-10%20133%20-10H127Q78%20-10%2057%2016T35%2071Q35%20103%2054%20123T99%20143Q142%20143%20142%20101Q142%2081%20130%2066T107%2046T94%2041L91%2040Q91%2039%2097%2036T113%2029T132%2026Q168%2026%20194%2071Q203%2087%20217%20139T245%20247T261%20313Q266%20340%20266%20352Q266%20380%20251%20392T217%20404Q177%20404%20142%20372T93%20290Q91%20281%2088%20280T72%20278H58Q52%20284%2052%20289Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-29%22%20d%3D%22M60%20749L64%20750Q69%20750%2074%20750H86L114%20726Q208%20641%20251%20514T294%20250Q294%20182%20284%20119T261%2012T224%20-76T186%20-143T145%20-194T113%20-227T90%20-246Q87%20-249%2086%20-250H74Q66%20-250%2063%20-250T58%20-247T55%20-238Q56%20-237%2066%20-225Q221%20-64%20221%20250T66%20725Q56%20737%2055%20738Q55%20746%2060%20749Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-5D%22%20d%3D%22M22%20710V750H159V-250H22V-210H119V710H22Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJSZ3-5B%22%20d%3D%22M247%20-949V1450H516V1388H309V-887H516V-949H247Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJSZ3-5D%22%20d%3D%22M11%201388V1450H280V-949H11V-887H218V1388H11Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-31%22%20d%3D%22M213%20578L200%20573Q186%20568%20160%20563T102%20556H83V602H102Q149%20604%20189%20617T245%20641T273%20663Q275%20666%20285%20666Q294%20666%20302%20660V361L303%2061Q310%2054%20315%2052T339%2048T401%2046H427V0H416Q395%203%20257%203Q121%203%20100%200H88V46H114Q136%2046%20152%2046T177%2047T193%2050T201%2052T207%2057T213%2061V578Z%22%3E%3C%2Fpath%3E%0A%3C%2Fdefs%3E%0A%3Cg%20stroke%3D%22currentColor%22%20fill%3D%22currentColor%22%20stroke-width%3D%220%22%20transform%3D%22matrix(1%200%200%20-1%200%200)%22%20aria-hidden%3D%22true%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-72%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(451%2C-150)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6D%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%22878%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-3D%22%20x%3D%221694%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2212%22%20x%3D%222751%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(3529%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJSZ3-5B%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(528%2C0)%22%3E%0A%3Cg%20transform%3D%22translate(120%2C0)%22%3E%0A%3Crect%20stroke%3D%22none%22%20width%3D%226007%22%20height%3D%2260%22%20x%3D%220%22%20y%3D%22220%22%3E%3C%2Frect%3E%0A%3Cg%20transform%3D%22translate(60%2C770)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2202%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-4C%22%20x%3D%22567%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(1415%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(389%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-79%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%22693%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%20x%3D%221224%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-66%22%20x%3D%221669%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(2386%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(389%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-78%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%22809%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%221306%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%224082%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(1513%2C-771)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2202%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-66%22%20x%3D%22567%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(1284%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(389%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-78%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%22809%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%221306%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJSZ3-5D%22%20x%3D%226776%22%20y%3D%22-1%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(7304%2C-1057)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-66%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%22550%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-78%22%20x%3D%22940%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%221512%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-3D%22%20x%3D%221902%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(1895%2C0)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-66%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(346%2C-175)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.574)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6D%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.574)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-2212%22%20x%3D%22878%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.574)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%221657%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%225022%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-78%22%20x%3D%225412%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%225984%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E#card=math&code=r%7Bm%20i%7D%3D-%5Cleft%5B%5Cfrac%7B%5Cpartial%20L%5Cleft%28y%7Bi%7D%2C%20f%5Cleft%28x%7Bi%7D%5Cright%29%5Cright%29%7D%7B%5Cpartial%20f%5Cleft%28x%7Bi%7D%5Cright%29%7D%5Cright%5D%7Bf%28x%29%3Df_%7Bm-1%7D%28x%29%7D&id=s2Eq0)
- 将
作为样本新的真实值拟合一个回归树,得到第m棵树的叶结点区域
。其中
为回归树t的叶子节点的个数。
- 对叶子区域j=1,2,…J,计算最佳拟合值:
%2Bc%5Cright)#card=math&code=c%7Bm%20j%7D%3D%5Carg%20%5Cmin%20%7Bc%7D%20%5Csum%7Bx%7Bi%7D%20%5Cin%20R%7Bm%20j%7D%7D%20L%5Cleft%28y%7Bi%7D%2C%20f%7Bm-1%7D%5Cleft%28x%7Bi%7D%5Cright%29%2Bc%5Cright%29&id=Z9hQO)
- 更新强学习器
%3Df%7Bm-1%7D(x)%2B%5Csum%7Bj%3D1%7D%5E%7BJ%7D%20c%7Bm%20j%7D%20I%5Cleft(x%20%5Cin%20R%7Bm%20j%7D%5Cright)#card=math&code=f%7Bm%7D%28x%29%3Df%7Bm-1%7D%28x%29%2B%5Csum%7Bj%3D1%7D%5E%7BJ%7D%20c%7Bm%20j%7D%20I%5Cleft%28x%20%5Cin%20R_%7Bm%20j%7D%5Cright%29&id=S99xL)
- 对每个样本i = 1,2,…,N计算负梯度,即残差:
得到回归树:
%3Df%7BM%7D(x)%3D%5Csum%7Bm%3D1%7D%5E%7BM%7D%20%5Csum%7Bj%3D1%7D%5E%7BJ%7D%20c%7Bm%20j%7D%20I%5Cleft(x%20%5Cin%20R%7Bm%20j%7D%5Cright)#card=math&code=%5Chat%7Bf%7D%28x%29%3Df%7BM%7D%28x%29%3D%5Csum%7Bm%3D1%7D%5E%7BM%7D%20%5Csum%7Bj%3D1%7D%5E%7BJ%7D%20c%7Bm%20j%7D%20I%5Cleft%28x%20%5Cin%20R%7Bm%20j%7D%5Cright%29&id=gjucA)
2.2.2 梯度提升法是如何运作的
下面,我们来使用一个具体的案例来说明GBDT是如何运作的(案例来源:https://blog.csdn.net/zpalyq110/article/details/79527653 ):
数据介绍:
如下表所示:一组数据,特征为年龄、体重,身高为标签值。共有5条数据,前四条为训练样本,最后一条为要预测的样本。
| 编号 | 年龄(岁) | 体重(kg) | 身高(m)(标签值) |
|---|---|---|---|
| 0 | 5 | 20 | 1.1 |
| 1 | 7 | 30 | 1.3 |
| 2 | 21 | 70 | 1.7 |
| 3 | 30 | 60 | 1.8 |
| 4(要预测的) | 25 | 65 | ? |
训练阶段:
参数设置:
- 学习率:learning_rate=0.1
- 迭代次数:n_trees=5
- 树的深度:max_depth=3
(1) 初始化弱学习器:
%3D%5Carg%20%5Cmin%20%7Bc%7D%20%5Csum%7Bi%3D1%7D%5E%7BN%7D%20L%5Cleft(y%7Bi%7D%2C%20c%5Cright)#card=math&code=f%7B0%7D%28x%29%3D%5Carg%20%5Cmin%20%7Bc%7D%20%5Csum%7Bi%3D1%7D%5E%7BN%7D%20L%5Cleft%28y_%7Bi%7D%2C%20c%5Cright%29&id=LFRaj)
损失函数为平方损失,因为平方损失函数是一个凸函数,直接求导,倒数等于零,得到 。
令导数等于0,即
得:
所以初始化时, 取值为所有训练样本标签值的均值:
此时得到初始学习器:
(2) 对于m=1,2,…,M:
由于我们设置了迭代次数:ntrees=5,这里的。
计算负梯度,根据上文损失函数为平方损失时,负梯度就是残差,再直白一点就是真实标签值 与上一轮得到的学习器的差值。
| 编号 | 年龄(岁) | 体重(kg) | 身高(m)( |
残差( |
|
|---|---|---|---|---|---|
| 0 | 5 | 20 | 1.1 | 1.475 | -0.375 |
| 1 | 7 | 30 | 1.3 | 1.475 | -0.175 |
| 2 | 21 | 70 | 1.7 | 1.475 | 0.225 |
| 3 | 30 | 60 | 1.8 | 1.475 | 0.325 |
学习决策树,分裂结点:
此时将残差作为样本的真实值来训练弱学习器,训练数据如下表:
| 编号 | 年龄(岁) | 体重(kg) | 身高(m)(标签值) |
|---|---|---|---|
| 0 | 5 | 20 | -0.375 |
| 1 | 7 | 30 | -0.175 |
| 2 | 21 | 70 | 0.225 |
| 3 | 30 | 60 | 0.325 |
接着,寻找回归树的最佳划分节点,遍历每个特征的每个可能取值。从年龄特征的5开始,到体重特征的70结束,分别计算分裂后两组数据的平方损失(Square Error),左节点平方损失,
右节点平方损失,找到使平方损失和
最小的那个划分节点,即为最佳划分节点。
例如:以年龄7为划分节点,将小于7的样本划分为到左节点,大于等于7的样本划分为右节点。左节点包括,右节点包括样本
,
,
,
。
所有可划分节点如下表:
| 划分点 | 小于划分点的样本 | 大于等于划分点的样本 | |||
|---|---|---|---|---|---|
| 年龄5 | / | 0,1,2,3 | 0 | 0.327 | 0.327 |
| 年龄7 | 0 | 1,2,3 | 0 | 0.140 | 0.140 |
| 年龄21 | 0,1 | 2,3 | 0.020 | 0.005 | 0.025 |
| 年龄30 | 0,1,2 | 3 | 0.187 | 0 | 0.187 |
| 体重20 | / | 0,1,2,3 | 0 | 0.327 | 0.327 |
| 体重30 | 0 | 1,2,3 | 0 | 0.140 | 0.140 |
| 体重60 | 0,1 | 2,3 | 0.020 | 0.005 | 0.025 |
| 体重70 | 0,1,3 | 2 | 0.260 | 0 | 0.260 |
以上划分点是的总平方损失最小为0.025有两个划分点:年龄21和体重60,所以随机选一个作为划分点,这里我们选 年龄21 。
现在我们的第一棵树长这个样子: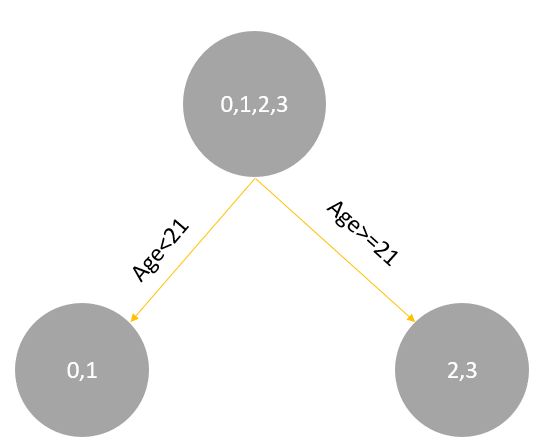
我们设置的参数中树的深度max_depth=3,现在树的深度只有2,需要再进行一次划分,这次划分要对左右两个节点分别进行划分:
对于左节点,只有0,1两个样本,那么根据下表我们选择年龄7进行划分:
| 划分点 | 小于划分点的样本 | 大于等于划分点的样本 | |||
|---|---|---|---|---|---|
| 年龄5 | / | 0,1 | 0 | 0.020 | 0.020 |
| 年龄7 | 0 | 1 | 0 | 0 | 0 |
| 体重20 | / | 0,1 | 0 | 0.020 | 0.020 |
| 体重30 | 0 | 1 | 0 | 0 | 0 |
对于右节点,只含有2,3两个样本,根据下表我们选择年龄30划分(也可以选体重70)
| 划分点 | 小于划分点的样本 | 大于等于划分点的样本 | |||
|---|---|---|---|---|---|
| 年龄21 | / | 2,3 | 0 | 0.005 | 0.005 |
| 年龄30 | 2 | 3 | 0 | 0 | 0 |
| 体重60 | / | 2,3 | 0 | 0.005 | 0.005 |
| 体重70 | 3 | 2 | 0 | 0 | 0 |
现在我们的第一棵树长这个样子: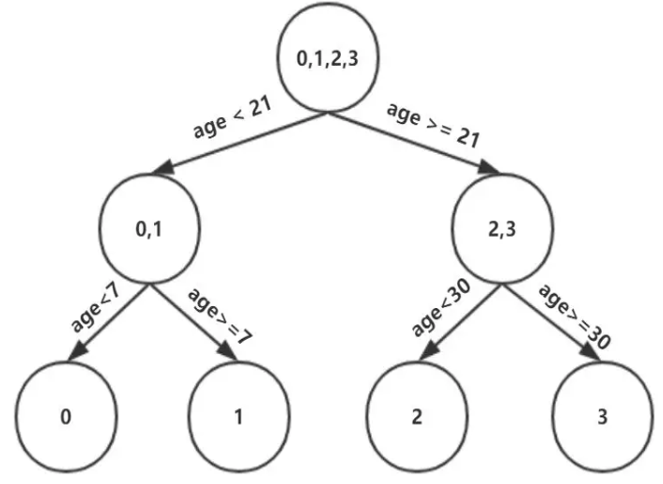
此时我们的树深度满足了设置,还需要做一件事情,给这每个叶子节点分别赋一个参数来拟合残差。
%2B%5CUpsilon%5Cright)%3C%2Ftitle%3E%0A%3Cdefs%20aria-hidden%3D%22true%22%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-3A5%22%20d%3D%22M55%20551Q55%20604%2091%20654T194%20705Q240%20705%20277%20681T334%20624T367%20556T385%20498L389%20474L392%20488Q394%20501%20400%20521T414%20566T438%20615T473%20659T521%20692T584%20705Q620%20705%20648%20689T691%20647T714%20597T722%20551Q722%20540%20719%20538T699%20536Q680%20536%20677%20541Q677%20542%20677%20544T676%20548Q676%20576%20650%20596T588%20616H582Q538%20616%20505%20582Q466%20543%20454%20477T441%20318Q441%20301%20441%20269T442%20222V61Q448%2055%20452%2053T478%2048T542%2046H569V0H557Q533%203%20389%203T221%200H209V46H236Q256%2046%20270%2046T295%2047T311%2048T322%2051T328%2054T332%2057T337%2061V209Q337%20383%20333%20415Q313%20616%20189%20616Q154%20616%20128%20597T101%20548Q101%20540%2097%20538T78%20536Q63%20536%2059%20538T55%20551Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-6A%22%20d%3D%22M297%20596Q297%20627%20318%20644T361%20661Q378%20661%20389%20651T403%20623Q403%20595%20384%20576T340%20557Q322%20557%20310%20567T297%20596ZM288%20376Q288%20405%20262%20405Q240%20405%20220%20393T185%20362T161%20325T144%20293L137%20279Q135%20278%20121%20278H107Q101%20284%20101%20286T105%20299Q126%20348%20164%20391T252%20441Q253%20441%20260%20441T272%20442Q296%20441%20316%20432Q341%20418%20354%20401T367%20348V332L318%20133Q267%20-67%20264%20-75Q246%20-125%20194%20-164T75%20-204Q25%20-204%207%20-183T-12%20-137Q-12%20-110%207%20-91T53%20-71Q70%20-71%2082%20-81T95%20-112Q95%20-148%2063%20-167Q69%20-168%2077%20-168Q111%20-168%20139%20-140T182%20-74L193%20-32Q204%2011%20219%2072T251%20197T278%20308T289%20365Q289%20372%20288%20376Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-31%22%20d%3D%22M213%20578L200%20573Q186%20568%20160%20563T102%20556H83V602H102Q149%20604%20189%20617T245%20641T273%20663Q275%20666%20285%20666Q294%20666%20302%20660V361L303%2061Q310%2054%20315%2052T339%2048T401%2046H427V0H416Q395%203%20257%203Q121%203%20100%200H88V46H114Q136%2046%20152%2046T177%2047T193%2050T201%2052T207%2057T213%2061V578Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-3D%22%20d%3D%22M56%20347Q56%20360%2070%20367H707Q722%20359%20722%20347Q722%20336%20708%20328L390%20327H72Q56%20332%2056%20347ZM56%20153Q56%20168%2072%20173H708Q722%20163%20722%20153Q722%20140%20707%20133H70Q56%20140%2056%20153Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-61%22%20d%3D%22M137%20305T115%20305T78%20320T63%20359Q63%20394%2097%20421T218%20448Q291%20448%20336%20416T396%20340Q401%20326%20401%20309T402%20194V124Q402%2076%20407%2058T428%2040Q443%2040%20448%2056T453%20109V145H493V106Q492%2066%20490%2059Q481%2029%20455%2012T400%20-6T353%2012T329%2054V58L327%2055Q325%2052%20322%2049T314%2040T302%2029T287%2017T269%206T247%20-2T221%20-8T190%20-11Q130%20-11%2082%2020T34%20107Q34%20128%2041%20147T68%20188T116%20225T194%20253T304%20268H318V290Q318%20324%20312%20340Q290%20411%20215%20411Q197%20411%20181%20410T156%20406T148%20403Q170%20388%20170%20359Q170%20334%20154%20320ZM126%20106Q126%2075%20150%2051T209%2026Q247%2026%20276%2049T315%20109Q317%20116%20318%20175Q318%20233%20317%20233Q309%20233%20296%20232T251%20223T193%20203T147%20166T126%20106Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-72%22%20d%3D%22M36%2046H50Q89%2046%2097%2060V68Q97%2077%2097%2091T98%20122T98%20161T98%20203Q98%20234%2098%20269T98%20328L97%20351Q94%20370%2083%20376T38%20385H20V408Q20%20431%2022%20431L32%20432Q42%20433%2060%20434T96%20436Q112%20437%20131%20438T160%20441T171%20442H174V373Q213%20441%20271%20441H277Q322%20441%20343%20419T364%20373Q364%20352%20351%20337T313%20322Q288%20322%20276%20338T263%20372Q263%20381%20265%20388T270%20400T273%20405Q271%20407%20250%20401Q234%20393%20226%20386Q179%20341%20179%20207V154Q179%20141%20179%20127T179%20101T180%2081T180%2066V61Q181%2059%20183%2057T188%2054T193%2051T200%2049T207%2048T216%2047T225%2047T235%2046T245%2046H276V0H267Q249%203%20140%203Q37%203%2028%200H20V46H36Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-67%22%20d%3D%22M329%20409Q373%20453%20429%20453Q459%20453%20472%20434T485%20396Q485%20382%20476%20371T449%20360Q416%20360%20412%20390Q410%20404%20415%20411Q415%20412%20416%20414V415Q388%20412%20363%20393Q355%20388%20355%20386Q355%20385%20359%20381T368%20369T379%20351T388%20325T392%20292Q392%20230%20343%20187T222%20143Q172%20143%20123%20171Q112%20153%20112%20133Q112%2098%20138%2081Q147%2075%20155%2075T227%2073Q311%2072%20335%2067Q396%2058%20431%2026Q470%20-13%20470%20-72Q470%20-139%20392%20-175Q332%20-206%20250%20-206Q167%20-206%20107%20-175Q29%20-140%2029%20-75Q29%20-39%2050%20-15T92%2018L103%2024Q67%2055%2067%20108Q67%20155%2096%20193Q52%20237%2052%20292Q52%20355%20102%20398T223%20442Q274%20442%20318%20416L329%20409ZM299%20343Q294%20371%20273%20387T221%20404Q192%20404%20171%20388T145%20343Q142%20326%20142%20292Q142%20248%20149%20227T179%20192Q196%20182%20222%20182Q244%20182%20260%20189T283%20207T294%20227T299%20242Q302%20258%20302%20292T299%20343ZM403%20-75Q403%20-50%20389%20-34T348%20-11T299%20-2T245%200H218Q151%200%20138%20-6Q118%20-15%20107%20-34T95%20-74Q95%20-84%20101%20-97T122%20-127T170%20-155T250%20-167Q319%20-167%20361%20-139T403%20-75Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-6D%22%20d%3D%22M41%2046H55Q94%2046%20102%2060V68Q102%2077%20102%2091T102%20122T103%20161T103%20203Q103%20234%20103%20269T102%20328V351Q99%20370%2088%20376T43%20385H25V408Q25%20431%2027%20431L37%20432Q47%20433%2065%20434T102%20436Q119%20437%20138%20438T167%20441T178%20442H181V402Q181%20364%20182%20364T187%20369T199%20384T218%20402T247%20421T285%20437Q305%20442%20336%20442Q351%20442%20364%20440T387%20434T406%20426T421%20417T432%20406T441%20395T448%20384T452%20374T455%20366L457%20361L460%20365Q463%20369%20466%20373T475%20384T488%20397T503%20410T523%20422T546%20432T572%20439T603%20442Q729%20442%20740%20329Q741%20322%20741%20190V104Q741%2066%20743%2059T754%2049Q775%2046%20803%2046H819V0H811L788%201Q764%202%20737%202T699%203Q596%203%20587%200H579V46H595Q656%2046%20656%2062Q657%2064%20657%20200Q656%20335%20655%20343Q649%20371%20635%20385T611%20402T585%20404Q540%20404%20506%20370Q479%20343%20472%20315T464%20232V168V108Q464%2078%20465%2068T468%2055T477%2049Q498%2046%20526%2046H542V0H534L510%201Q487%202%20460%202T422%203Q319%203%20310%200H302V46H318Q379%2046%20379%2062Q380%2064%20380%20200Q379%20335%20378%20343Q372%20371%20358%20385T334%20402T308%20404Q263%20404%20229%20370Q202%20343%20195%20315T187%20232V168V108Q187%2078%20188%2068T191%2055T200%2049Q221%2046%20249%2046H265V0H257L234%201Q210%202%20183%202T145%203Q42%203%2033%200H25V46H41Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-69%22%20d%3D%22M69%20609Q69%20637%2087%20653T131%20669Q154%20667%20171%20652T188%20609Q188%20579%20171%20564T129%20549Q104%20549%2087%20564T69%20609ZM247%200Q232%203%20143%203Q132%203%20106%203T56%201L34%200H26V46H42Q70%2046%2091%2049Q100%2053%20102%2060T104%20102V205V293Q104%20345%20102%20359T88%20378Q74%20385%2041%20385H30V408Q30%20431%2032%20431L42%20432Q52%20433%2070%20434T106%20436Q123%20437%20142%20438T171%20441T182%20442H185V62Q190%2052%20197%2050T232%2046H255V0H247Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-6E%22%20d%3D%22M41%2046H55Q94%2046%20102%2060V68Q102%2077%20102%2091T102%20122T103%20161T103%20203Q103%20234%20103%20269T102%20328V351Q99%20370%2088%20376T43%20385H25V408Q25%20431%2027%20431L37%20432Q47%20433%2065%20434T102%20436Q119%20437%20138%20438T167%20441T178%20442H181V402Q181%20364%20182%20364T187%20369T199%20384T218%20402T247%20421T285%20437Q305%20442%20336%20442Q450%20438%20463%20329Q464%20322%20464%20190V104Q464%2066%20466%2059T477%2049Q498%2046%20526%2046H542V0H534L510%201Q487%202%20460%202T422%203Q319%203%20310%200H302V46H318Q379%2046%20379%2062Q380%2064%20380%20200Q379%20335%20378%20343Q372%20371%20358%20385T334%20402T308%20404Q263%20404%20229%20370Q202%20343%20195%20315T187%20232V168V108Q187%2078%20188%2068T191%2055T200%2049Q221%2046%20249%2046H265V0H257L234%201Q210%202%20183%202T145%203Q42%203%2033%200H25V46H41Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJSZ4-E152%22%20d%3D%22M-24%20327L-18%20333H-1Q11%20333%2015%20333T22%20329T27%20322T35%20308T54%20284Q115%20203%20225%20162T441%20120Q454%20120%20457%20117T460%2095V60V28Q460%208%20457%204T442%200Q355%200%20260%2036Q75%20118%20-16%20278L-24%20292V327Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJSZ4-E153%22%20d%3D%22M-10%2060V95Q-10%20113%20-7%20116T9%20120Q151%20120%20250%20171T396%20284Q404%20293%20412%20305T424%20324T431%20331Q433%20333%20451%20333H468L474%20327V292L466%20278Q375%20118%20190%2036Q95%200%208%200Q-5%200%20-7%203T-10%2024V60Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJSZ4-E151%22%20d%3D%22M-10%2060Q-10%20104%20-10%20111T-5%20118Q-1%20120%2010%20120Q96%20120%20190%2084Q375%202%20466%20-158L474%20-172V-207L468%20-213H451H447Q437%20-213%20434%20-213T428%20-209T423%20-202T414%20-187T396%20-163Q331%20-82%20224%20-41T9%200Q-4%200%20-7%203T-10%2025V60Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJSZ4-E150%22%20d%3D%22M-18%20-213L-24%20-207V-172L-16%20-158Q75%202%20260%2084Q334%20113%20415%20119Q418%20119%20427%20119T440%20120Q454%20120%20457%20117T460%2098V60V25Q460%207%20457%204T441%200Q308%200%20193%20-55T25%20-205Q21%20-211%2018%20-212T-1%20-213H-18Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJSZ4-E154%22%20d%3D%22M-10%200V120H410V0H-10Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJSZ2-2211%22%20d%3D%22M60%20948Q63%20950%20665%20950H1267L1325%20815Q1384%20677%201388%20669H1348L1341%20683Q1320%20724%201285%20761Q1235%20809%201174%20838T1033%20881T882%20898T699%20902H574H543H251L259%20891Q722%20258%20724%20252Q725%20250%20724%20246Q721%20243%20460%20-56L196%20-356Q196%20-357%20407%20-357Q459%20-357%20548%20-357T676%20-358Q812%20-358%20896%20-353T1063%20-332T1204%20-283T1307%20-196Q1328%20-170%201348%20-124H1388Q1388%20-125%201381%20-145T1356%20-210T1325%20-294L1267%20-449L666%20-450Q64%20-450%2061%20-448Q55%20-446%2055%20-439Q55%20-437%2057%20-433L590%20177Q590%20178%20557%20222T452%20366T322%20544L56%20909L55%20924Q55%20945%2060%20948Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-78%22%20d%3D%22M52%20289Q59%20331%20106%20386T222%20442Q257%20442%20286%20424T329%20379Q371%20442%20430%20442Q467%20442%20494%20420T522%20361Q522%20332%20508%20314T481%20292T458%20288Q439%20288%20427%20299T415%20328Q415%20374%20465%20391Q454%20404%20425%20404Q412%20404%20406%20402Q368%20386%20350%20336Q290%20115%20290%2078Q290%2050%20306%2038T341%2026Q378%2026%20414%2059T463%20140Q466%20150%20469%20151T485%20153H489Q504%20153%20504%20145Q504%20144%20502%20134Q486%2077%20440%2033T333%20-11Q263%20-11%20227%2052Q186%20-10%20133%20-10H127Q78%20-10%2057%2016T35%2071Q35%20103%2054%20123T99%20143Q142%20143%20142%20101Q142%2081%20130%2066T107%2046T94%2041L91%2040Q91%2039%2097%2036T113%2029T132%2026Q168%2026%20194%2071Q203%2087%20217%20139T245%20247T261%20313Q266%20340%20266%20352Q266%20380%20251%20392T217%20404Q177%20404%20142%20372T93%20290Q91%20281%2088%20280T72%20278H58Q52%20284%2052%20289Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-69%22%20d%3D%22M184%20600Q184%20624%20203%20642T247%20661Q265%20661%20277%20649T290%20619Q290%20596%20270%20577T226%20557Q211%20557%20198%20567T184%20600ZM21%20287Q21%20295%2030%20318T54%20369T98%20420T158%20442Q197%20442%20223%20419T250%20357Q250%20340%20236%20301T196%20196T154%2083Q149%2061%20149%2051Q149%2026%20166%2026Q175%2026%20185%2029T208%2043T235%2078T260%20137Q263%20149%20265%20151T282%20153Q302%20153%20302%20143Q302%20135%20293%20112T268%2061T223%2011T161%20-11Q129%20-11%20102%2010T74%2074Q74%2091%2079%20106T122%20220Q160%20321%20166%20341T173%20380Q173%20404%20156%20404H154Q124%20404%2099%20371T61%20287Q60%20286%2059%20284T58%20281T56%20279T53%20278T49%20278T41%20278H27Q21%20284%2021%20287Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-2208%22%20d%3D%22M84%20250Q84%20372%20166%20450T360%20539Q361%20539%20377%20539T419%20540T469%20540H568Q583%20532%20583%20520Q583%20511%20570%20501L466%20500Q355%20499%20329%20494Q280%20482%20242%20458T183%20409T147%20354T129%20306T124%20272V270H568Q583%20262%20583%20250T568%20230H124V228Q124%20207%20134%20177T167%20112T231%2048T328%207Q355%201%20466%200H570Q583%20-10%20583%20-20Q583%20-32%20568%20-40H471Q464%20-40%20446%20-40T417%20-41Q262%20-41%20172%2045Q84%20127%2084%20250Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-52%22%20d%3D%22M230%20637Q203%20637%20198%20638T193%20649Q193%20676%20204%20682Q206%20683%20378%20683Q550%20682%20564%20680Q620%20672%20658%20652T712%20606T733%20563T739%20529Q739%20484%20710%20445T643%20385T576%20351T538%20338L545%20333Q612%20295%20612%20223Q612%20212%20607%20162T602%2080V71Q602%2053%20603%2043T614%2025T640%2016Q668%2016%20686%2038T712%2085Q717%2099%20720%20102T735%20105Q755%20105%20755%2093Q755%2075%20731%2036Q693%20-21%20641%20-21H632Q571%20-21%20531%204T487%2082Q487%20109%20502%20166T517%20239Q517%20290%20474%20313Q459%20320%20449%20321T378%20323H309L277%20193Q244%2061%20244%2059Q244%2055%20245%2054T252%2050T269%2048T302%2046H333Q339%2038%20339%2037T336%2019Q332%206%20326%200H311Q275%202%20180%202Q146%202%20117%202T71%202T50%201Q33%201%2033%2010Q33%2012%2036%2024Q41%2043%2046%2045Q50%2046%2061%2046H67Q94%2046%20127%2049Q141%2052%20146%2061Q149%2065%20218%20339T287%20628Q287%20635%20230%20637ZM630%20554Q630%20586%20609%20608T523%20636Q521%20636%20500%20636T462%20637H440Q393%20637%20386%20627Q385%20624%20352%20494T319%20361Q319%20360%20388%20360Q466%20361%20492%20367Q556%20377%20592%20426Q608%20449%20619%20486T630%20554Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-4C%22%20d%3D%22M228%20637Q194%20637%20192%20641Q191%20643%20191%20649Q191%20673%20202%20682Q204%20683%20217%20683Q271%20680%20344%20680Q485%20680%20506%20683H518Q524%20677%20524%20674T522%20656Q517%20641%20513%20637H475Q406%20636%20394%20628Q387%20624%20380%20600T313%20336Q297%20271%20279%20198T252%2088L243%2052Q243%2048%20252%2048T311%2046H328Q360%2046%20379%2047T428%2054T478%2072T522%20106T564%20161Q580%20191%20594%20228T611%20270Q616%20273%20628%20273H641Q647%20264%20647%20262T627%20203T583%2083T557%209Q555%204%20553%203T537%200T494%20-1Q483%20-1%20418%20-1T294%200H116Q32%200%2032%2010Q32%2017%2034%2024Q39%2043%2044%2045Q48%2046%2059%2046H65Q92%2046%20125%2049Q139%2052%20144%2061Q147%2065%20216%20339T285%20628Q285%20635%20228%20637Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-28%22%20d%3D%22M94%20250Q94%20319%20104%20381T127%20488T164%20576T202%20643T244%20695T277%20729T302%20750H315H319Q333%20750%20333%20741Q333%20738%20316%20720T275%20667T226%20581T184%20443T167%20250T184%2058T225%20-81T274%20-167T316%20-220T333%20-241Q333%20-250%20318%20-250H315H302L274%20-226Q180%20-141%20137%20-14T94%20250Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-79%22%20d%3D%22M21%20287Q21%20301%2036%20335T84%20406T158%20442Q199%20442%20224%20419T250%20355Q248%20336%20247%20334Q247%20331%20231%20288T198%20191T182%20105Q182%2062%20196%2045T238%2027Q261%2027%20281%2038T312%2061T339%2094Q339%2095%20344%20114T358%20173T377%20247Q415%20397%20419%20404Q432%20431%20462%20431Q475%20431%20483%20424T494%20412T496%20403Q496%20390%20447%20193T391%20-23Q363%20-106%20294%20-155T156%20-205Q111%20-205%2077%20-183T43%20-117Q43%20-95%2050%20-80T69%20-58T89%20-48T106%20-45Q150%20-45%20150%20-87Q150%20-107%20138%20-122T115%20-142T102%20-147L99%20-148Q101%20-153%20118%20-160T152%20-167H160Q177%20-167%20186%20-165Q219%20-156%20247%20-127T290%20-65T313%20-9T321%2021L315%2017Q309%2013%20296%206T270%20-6Q250%20-11%20231%20-11Q185%20-11%20150%2011T104%2082Q103%2089%20103%20113Q103%20170%20138%20262T173%20379Q173%20380%20173%20381Q173%20390%20173%20393T169%20400T158%20404H154Q131%20404%20112%20385T82%20344T65%20302T57%20280Q55%20278%2041%20278H27Q21%20284%2021%20287Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-2C%22%20d%3D%22M78%2035T78%2060T94%20103T137%20121Q165%20121%20187%2096T210%208Q210%20-27%20201%20-60T180%20-117T154%20-158T130%20-185T117%20-194Q113%20-194%20104%20-185T95%20-172Q95%20-168%20106%20-156T131%20-126T157%20-76T173%20-3V9L172%208Q170%207%20167%206T161%203T152%201T140%200Q113%200%2096%2017Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-66%22%20d%3D%22M118%20-162Q120%20-162%20124%20-164T135%20-167T147%20-168Q160%20-168%20171%20-155T187%20-126Q197%20-99%20221%2027T267%20267T289%20382V385H242Q195%20385%20192%20387Q188%20390%20188%20397L195%20425Q197%20430%20203%20430T250%20431Q298%20431%20298%20432Q298%20434%20307%20482T319%20540Q356%20705%20465%20705Q502%20703%20526%20683T550%20630Q550%20594%20529%20578T487%20561Q443%20561%20443%20603Q443%20622%20454%20636T478%20657L487%20662Q471%20668%20457%20668Q445%20668%20434%20658T419%20630Q412%20601%20403%20552T387%20469T380%20433Q380%20431%20435%20431Q480%20431%20487%20430T498%20424Q499%20420%20496%20407T491%20391Q489%20386%20482%20386T428%20385H372L349%20263Q301%2015%20282%20-47Q255%20-132%20212%20-173Q175%20-205%20139%20-205Q107%20-205%2081%20-186T55%20-132Q55%20-95%2076%20-78T118%20-61Q162%20-61%20162%20-103Q162%20-122%20151%20-136T127%20-157L118%20-162Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-30%22%20d%3D%22M96%20585Q152%20666%20249%20666Q297%20666%20345%20640T423%20548Q460%20465%20460%20320Q460%20165%20417%2083Q397%2041%20362%2016T301%20-15T250%20-22Q224%20-22%20198%20-16T137%2016T82%2083Q39%20165%2039%20320Q39%20494%2096%20585ZM321%20597Q291%20629%20250%20629Q208%20629%20178%20597Q153%20571%20145%20525T137%20333Q137%20175%20145%20125T181%2046Q209%2016%20250%2016Q290%2016%20318%2046Q347%2076%20354%20130T362%20333Q362%20478%20354%20524T321%20597Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-29%22%20d%3D%22M60%20749L64%20750Q69%20750%2074%20750H86L114%20726Q208%20641%20251%20514T294%20250Q294%20182%20284%20119T261%2012T224%20-76T186%20-143T145%20-194T113%20-227T90%20-246Q87%20-249%2086%20-250H74Q66%20-250%2063%20-250T58%20-247T55%20-238Q56%20-237%2066%20-225Q221%20-64%20221%20250T66%20725Q56%20737%2055%20738Q55%20746%2060%20749Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-2B%22%20d%3D%22M56%20237T56%20250T70%20270H369V420L370%20570Q380%20583%20389%20583Q402%20583%20409%20568V270H707Q722%20262%20722%20250T707%20230H409V-68Q401%20-82%20391%20-82H389H387Q375%20-82%20369%20-68V230H70Q56%20237%2056%20250Z%22%3E%3C%2Fpath%3E%0A%3C%2Fdefs%3E%0A%3Cg%20stroke%3D%22currentColor%22%20fill%3D%22currentColor%22%20stroke-width%3D%220%22%20transform%3D%22matrix(1%200%200%20-1%200%200)%22%20aria-hidden%3D%22true%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-3A5%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(778%2C-150)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6A%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%22412%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-3D%22%20x%3D%221801%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(2858%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-61%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-72%22%20x%3D%22500%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-67%22%20x%3D%22893%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(1560%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-6D%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-69%22%20x%3D%22833%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-6E%22%20x%3D%221112%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(12%2C-721)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJSZ4-E152%22%20x%3D%2223%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(499.37718253968256%2C0)%20scale(1.6186507936507941%2C1)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJSZ4-E154%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(1163%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJSZ4-E151%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJSZ4-E150%22%20x%3D%22450%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(2080.210515873016%2C0)%20scale(1.6186507936507941%2C1)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJSZ4-E154%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJSZ4-E153%22%20x%3D%222754%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-3A5%22%20x%3D%221893%22%20y%3D%22-2264%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(6253%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJSZ2-2211%22%20x%3D%22416%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(0%2C-1102)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-78%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.574)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%22705%22%20y%3D%22-238%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-2208%22%20x%3D%22952%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(1145%2C0)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-52%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(537%2C-140)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.574)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6A%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.574)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%22412%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-4C%22%20x%3D%228697%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(9546%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(389%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-79%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%22693%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%20x%3D%221224%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(1669%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-66%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-30%22%20x%3D%22693%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(2780%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(389%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-78%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%22809%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%221306%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%224698%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-3A5%22%20x%3D%225699%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%226477%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E#card=math&code=%5CUpsilon%7Bj%201%7D%3D%5Cunderbrace%7B%5Carg%20%5Cmin%20%7D%7B%5CUpsilon%7D%20%5Csum%7Bx%7Bi%7D%20%5Cin%20R%7Bj%201%7D%7D%20L%5Cleft%28y%7Bi%7D%2C%20f%7B0%7D%5Cleft%28x%7Bi%7D%5Cright%29%2B%5CUpsilon%5Cright%29&id=m6ptc):
这里其实和上面初始化学习器是一个道理,平方损失,求导,令导数等于零,化简之后得到每个叶子节点的参数,其实就是标签值的均值。这个地方的标签值不是原始的
,而是本轮要拟合的标残差
根据上述划分结果,为了方便表示,规定从左到右为第1 , 2 , 3 , 4 个叶子结点
%2C%20%5Cquad%20%5CUpsilon%7B11%7D%3D-0.375%20%5C%5C%0A%5Cleft(x%7B1%7D%20%5Cin%20R%7B21%7D%5Cright)%2C%20%5Cquad%20%5CUpsilon%7B21%7D%3D-0.175%20%5C%5C%0A%5Cleft(x%7B2%7D%20%5Cin%20R%7B31%7D%5Cright)%2C%20%5Cquad%20%5CUpsilon%7B31%7D%3D0.225%20%5C%5C%0A%5Cleft(x%7B3%7D%20%5Cin%20R%7B41%7D%5Cright)%2C%20%5Cquad%20%5CUpsilon%7B41%7D%3D0.325%0A%5Cend%7Barray%7D%0A#card=math&code=%5Cbegin%7Barray%7D%7Bl%7D%0A%5Cleft%28x%7B0%7D%20%5Cin%20R%7B11%7D%5Cright%29%2C%20%5Cquad%20%5CUpsilon%7B11%7D%3D-0.375%20%5C%5C%0A%5Cleft%28x%7B1%7D%20%5Cin%20R%7B21%7D%5Cright%29%2C%20%5Cquad%20%5CUpsilon%7B21%7D%3D-0.175%20%5C%5C%0A%5Cleft%28x%7B2%7D%20%5Cin%20R%7B31%7D%5Cright%29%2C%20%5Cquad%20%5CUpsilon%7B31%7D%3D0.225%20%5C%5C%0A%5Cleft%28x%7B3%7D%20%5Cin%20R%7B41%7D%5Cright%29%2C%20%5Cquad%20%5CUpsilon%7B41%7D%3D0.325%0A%5Cend%7Barray%7D%0A&id=MTmWw)
此时的树模型结构如下: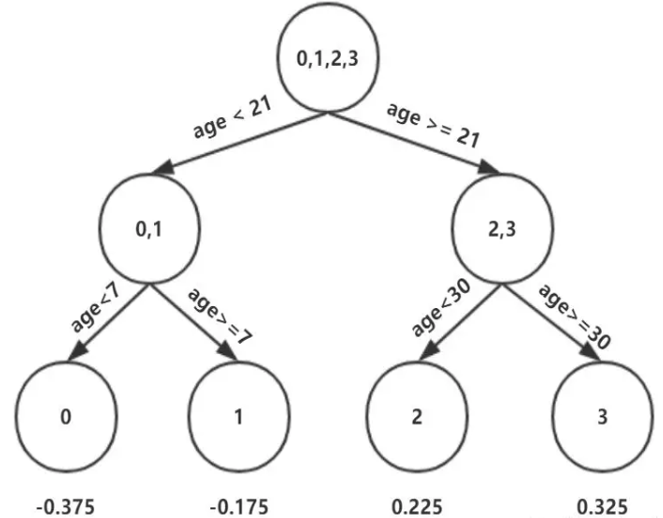
此时可更新强学习器,需要用到参数学习率:learningrate=0.1,用表示。

为什么要用学习率呢?这是Shrinkage的思想,如果每次都全部加上(学习率为1)很容易一步学到位导致过拟合。
最后得到五轮迭代: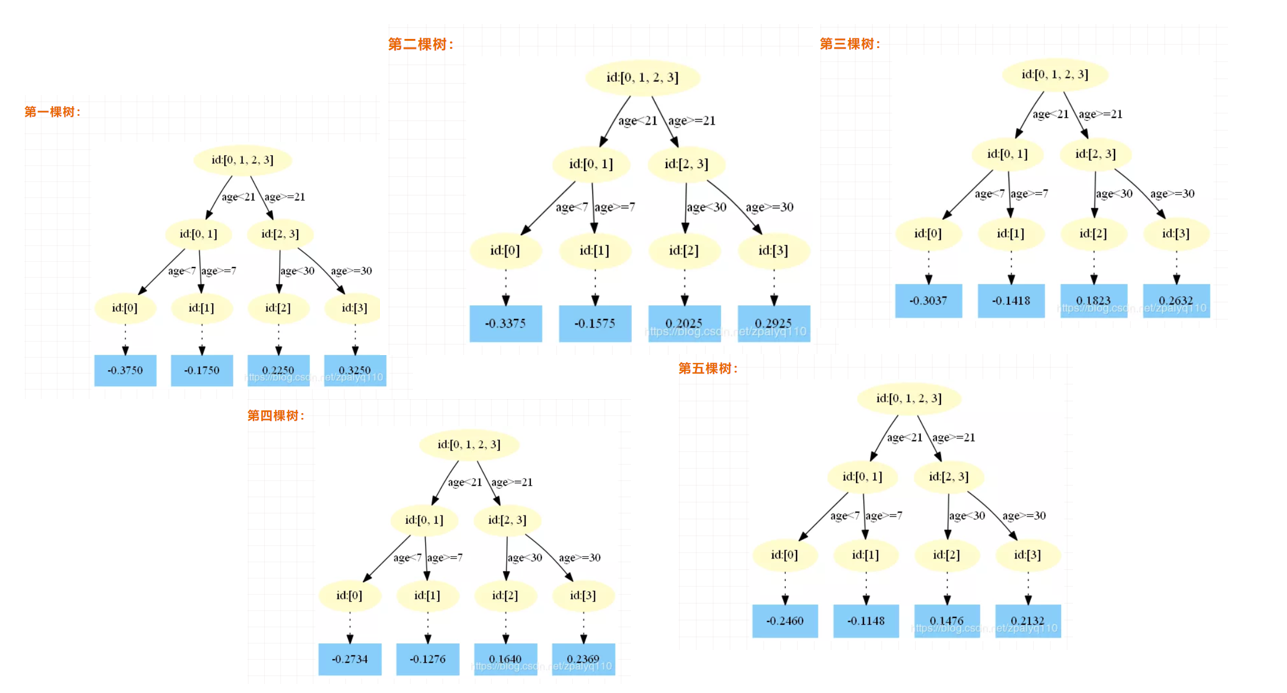
最后的强学习器为:%3Df%7B5%7D(x)%3Df%7B0%7D(x)%2B%5Csum%7Bm%3D1%7D%5E%7B5%7D%20%5Csum%7Bj%3D1%7D%5E%7B4%7D%20%5CUpsilon%7Bj%20m%7D%20I%5Cleft(x%20%5Cin%20R%7Bj%20m%7D%5Cright)#card=math&code=f%28x%29%3Df%7B5%7D%28x%29%3Df%7B0%7D%28x%29%2B%5Csum%7Bm%3D1%7D%5E%7B5%7D%20%5Csum%7Bj%3D1%7D%5E%7B4%7D%20%5CUpsilon%7Bj%20m%7D%20I%5Cleft%28x%20%5Cin%20R%7Bj%20m%7D%5Cright%29&id=Tr0zq)。
其中:
%3D1.475%20%26%20f%7B2%7D(x)%3D0.0205%20%5C%5C%0Af%7B3%7D(x)%3D0.1823%20%26%20f%7B4%7D(x)%3D0.1640%20%5C%5C%0Af%7B5%7D(x)%3D0.1476%0A%5Cend%7Barray%7D%0A#card=math&code=%5Cbegin%7Barray%7D%7Bll%7D%0Af%7B0%7D%28x%29%3D1.475%20%26%20f%7B2%7D%28x%29%3D0.0205%20%5C%5C%0Af%7B3%7D%28x%29%3D0.1823%20%26%20f%7B4%7D%28x%29%3D0.1640%20%5C%5C%0Af_%7B5%7D%28x%29%3D0.1476%0A%5Cend%7Barray%7D%0A&id=VZ9j8)
预测结果为:
%3D1.475%2B0.1%20*(0.2250%2B0.2025%2B0.1823%2B0.164%2B0.1476)%3D1.56714%0A#card=math&code=f%28x%29%3D1.475%2B0.1%20%2A%280.2250%2B0.2025%2B0.1823%2B0.164%2B0.1476%29%3D1.56714%0A&id=qfZBo)
3. 在sklearn中使用GDBT的实例
下面我们来使用sklearn来使用GBDT:
GradientBoostingRegressor参数解释:
- loss:{‘ls’, ‘lad’, ‘huber’, ‘quantile’}, default=’ls’:‘ls’ 指最小二乘回归. ‘lad’ (最小绝对偏差) 是仅基于输入变量的顺序信息的高度鲁棒的损失函数。. ‘huber’ 是两者的结合. ‘quantile’允许分位数回归(用于alpha指定分位数)
- learning_rate:学习率缩小了每棵树的贡献learning_rate。在learning_rate和n_estimators之间需要权衡。
- n_estimators:要执行的提升次数。
- subsample:用于拟合各个基础学习者的样本比例。如果小于1.0,则将导致随机梯度增强。subsample与参数n_estimators。选择会导致方差减少和偏差增加。subsample < 1.0
- criterion:{‘friedman_mse’,’mse’,’mae’},默认=’friedman_mse’:“ mse”是均方误差,“ mae”是平均绝对误差。默认值“ friedman_mse”通常是最好的,因为在某些情况下它可以提供更好的近似值。
- min_samples_split:拆分内部节点所需的最少样本数
- min_samples_leaf:在叶节点处需要的最小样本数。
- min_weight_fraction_leaf:在所有叶节点处(所有输入样本)的权重总和中的最小加权分数。如果未提供sample_weight,则样本的权重相等。
- max_depth:各个回归模型的最大深度。最大深度限制了树中节点的数量。调整此参数以获得最佳性能;最佳值取决于输入变量的相互作用。
- min_impurity_decrease:如果节点分裂会导致杂质的减少大于或等于该值,则该节点将被分裂。
- min_impurity_split:提前停止树木生长的阈值。如果节点的杂质高于阈值,则该节点将分裂
- max_features{‘auto’, ‘sqrt’, ‘log2’},int或float:寻找最佳分割时要考虑的功能数量:
- 如果为int,则max_features在每个分割处考虑特征。
- 如果为float,max_features则为小数,并 在每次拆分时考虑要素。int(max_features * n_features)
- 如果“auto”,则max_features=n_features。
- 如果是“ sqrt”,则max_features=sqrt(n_features)。
- 如果为“ log2”,则为max_features=log2(n_features)。
- 如果没有,则max_features=n_features。
from sklearn.metrics import mean_squared_errorfrom sklearn.datasets import make_friedman1from sklearn.ensemble import GradientBoostingRegressorX, y = make_friedman1(n_samples=1200, random_state=0, noise=1.0)X_train, X_test = X[:200], X[200:]y_train, y_test = y[:200], y[200:]est = GradientBoostingRegressor(n_estimators=100, learning_rate=0.1,max_depth=1, random_state=0, loss='ls').fit(X_train, y_train)mean_squared_error(y_test, est.predict(X_test))
5.009154859960321
from sklearn.datasets import make_regressionfrom sklearn.ensemble import GradientBoostingRegressorfrom sklearn.model_selection import train_test_splitX, y = make_regression(random_state=0)X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)reg = GradientBoostingRegressor(random_state=0)reg.fit(X_train, y_train)reg.score(X_test, y_test)
0.4233836905173889
4. 小作业
这里给大家一个小作业,就是大家总结下GradientBoostingRegressor与GradientBoostingClassifier函数的各个参数的意思!参考文档:
GradientBoostingRegressor:
https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.GradientBoostingRegressor.html#sklearn.ensemble.GradientBoostingRegressorGradientBoostingClassifier:
https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.GradientBoostingClassifier.html?highlight=gra#sklearn.ensemble.GradientBoostingClassifier

