1. 投票法的思路

投票法是集成学习中常用的技巧，可以帮助我们提高模型的泛化能力，减少模型的错误率。举个例子，在航空航天领域，每个零件发出的电信号都对航空器的成功发射起到重要作用。如果我们有一个二进制形式的信号：
11101100100111001011011011011
在传输过程中第二位发生了翻转
10101100100111001011011011011

这导致的结果可能是致命的。一个常用的纠错方法是重复多次发送数据，并以少数服从多数的方法确定正确的传输数据。一般情况下，错误总是发生在局部，因此融合多个数据是降低误差的一个好方法，这就是投票法的基本思路。
对于回归模型来说，投票法最终的预测结果是多个其他回归模型预测结果的平均值。
对于分类模型，硬投票法的预测结果是多个模型预测结果中出现次数最多的类别，软投票对各类预测结果的概率进行求和，最终选取概率之和最大的类标签。

2. 投票法的原理分析

投票法是一种遵循少数服从多数原则的集成学习模型，通过多个模型的集成降低方差，从而提高模型的鲁棒性。在理想情况下，投票法的预测效果应当优于任何一个基模型的预测效果。

投票法在回归模型与分类模型上均可使用：

  • 回归投票法：预测结果是所有模型预测结果的平均值。
  • 分类投票法：预测结果是所有模型种出现最多的预测结果。

分类投票法又可以被划分为硬投票与软投票：

  • 硬投票：预测结果是所有投票结果最多出现的类。
  • 软投票：预测结果是所有投票结果中概率加和最大的类。

下面我们使用一个例子说明硬投票：

对于某个样本： 模型 1 的预测结果是 类别 A 模型 2 的预测结果是 类别 B 模型 3 的预测结果是 类别 B

有2/3的模型预测结果是B，因此硬投票法的预测结果是B
同样的例子说明软投票：

对于某个样本： 模型 1 的预测结果是 类别 A 的概率为 99% 模型 2 的预测结果是 类别 A 的概率为 49% 模型 3 的预测结果是 类别 A 的概率为 49%

最终对于类别A的预测概率的平均是 (99 + 49 + 49) / 3 = 65.67%，因此软投票法的预测结果是A。

从这个例子我们可以看出，软投票法与硬投票法可以得出完全不同的结论。相对于硬投票，软投票法考虑到了预测概率这一额外的信息，因此可以得出比硬投票法更加准确的预测结果。

在投票法中，我们还需要考虑到不同的基模型可能产生的影响。理论上，基模型可以是任何已被训练好的模型。但在实际应用上，想要投票法产生较好的结果，需要满足两个条件：

  • 基模型之间的效果不能差别过大。当某个基模型相对于其他基模型效果过差时，该模型很可能成为噪声。
  • 基模型之间应该有较小的同质性。例如在基模型预测效果近似的情况下，基于树模型与线性模型的投票，往往优于两个树模型或两个线性模型。

当投票合集中使用的模型能预测出清晰的类别标签时，适合使用硬投票。当投票集合中使用的模型能预测类别的概率时，适合使用软投票。软投票同样可以用于那些本身并不预测类成员概率的模型，只要他们可以输出类似于概率的预测分数值（例如支持向量机、k-最近邻和决策树）。

投票法的局限性在于，它对所有模型的处理是一样的，这意味着所有模型对预测的贡献是一样的。如果一些模型在某些情况下很好，而在其他情况下很差，这是使用投票法时需要考虑到的一个问题。

3. 投票法的案例分析(基于sklearn)

Sklearn中提供了 VotingRegressor 与 VotingClassifier 两个投票方法。 这两种模型的操作方式相同，并采用相同的参数。使用模型需要提供一个模型列表，列表中每个模型采用Tuple的结构表示，第一个元素代表名称，第二个元素代表模型，需要保证每个模型必须拥有唯一的名称。

例如这里，我们定义两个模型：

  1. models = [('lr',LogisticRegression()),('svm',SVC())]
  2. ensemble = VotingClassifier(estimators=models)

有时某些模型需要一些预处理操作，我们可以为他们定义Pipeline完成模型预处理工作：

  1. models = [('lr',LogisticRegression()),('svm',make_pipeline(StandardScaler(),SVC()))]
  2. ensemble = VotingClassifier(estimators=models)

模型还提供了voting参数让我们选择软投票或者硬投票：

  1. models = [('lr',LogisticRegression()),('svm',SVC())]
  2. ensemble = VotingClassifier(estimators=models, voting='soft')

下面我们使用一个完整的例子演示投票法的使用：
首先我们创建一个1000个样本，20个特征的随机数据集：

  1. # test classification dataset
  2. from sklearn.datasets import make_classification
  3. from sklearn.neighbors import KNeighborsClassifier
  4. from sklearn.ensemble import VotingClassifier
  5. from sklearn.model_selection import RepeatedStratifiedKFold, cross_val_score
  8. # define dataset
  9. X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=2)
  10. # summarize the dataset
  11. print(X.shape, y.shape)
  1. def get_dataset():
  2.     X, y = make_classification(n_samples=1000, n_features=20,
  3.                                n_informative=15, n_redundant=5, random_state=2)
  4.     return X, y

我们使用多个KNN模型作为基模型演示投票法，其中每个模型采用不同的邻居值K参数：

  1. # get a voting ensemble of models
  2. def get_voting():
  3.     # define the base models
  4.     models = list()
  5.     models.append(('knn1', KNeighborsClassifier(n_neighbors=1)))
  6.     models.append(('knn3', KNeighborsClassifier(n_neighbors=3)))
  7.     models.append(('knn5', KNeighborsClassifier(n_neighbors=5)))
  8.     models.append(('knn7', KNeighborsClassifier(n_neighbors=7)))
  9.     models.append(('knn9', KNeighborsClassifier(n_neighbors=9)))
  10.     # define the voting ensemble
  11.     ensemble = VotingClassifier(estimators=models, voting='hard')
  12.     return ensemble

下面的evaluate_model()函数接收一个模型实例，并以分层10倍交叉验证三次重复的分数列表的形式返回。

  1. # evaluate a give model using cross-validation
  2. def evaluate_model(model, X, y):
  3.     cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
  4.     scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise')
  5.     return scores

然后，我们可以报告每个算法的平均性能，还可以创建一个箱形图和须状图来比较每个算法的精度分数分布。

  1. from numpy import mean, std
  2. import matplotlib.pyplot as plt
  3. %matplotlib inline
  6. # X, y = get_dataset()
  7. # get the models to evaluate
  8. models = get_models()
  9. # evaluate the models and store results
  10. results, names = list(), list()
  11. for name, model in models.items():
  12.     scores = evaluate_model(model, X, y)
  13.     results.append(scores)
  14.     names.append(name)
  15.     print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores)))
  16. # plot model performance for comparison
  17. plt.boxplot(results, labels=names, showmeans=True)
  18. plt.show()

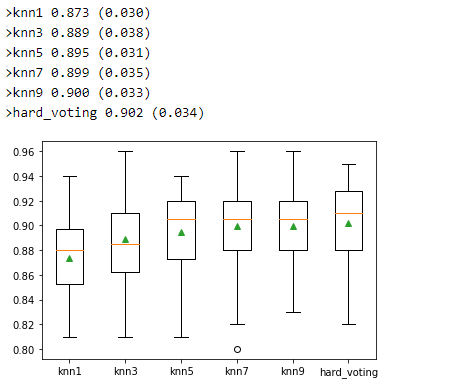
image.png
显然投票的效果略大于任何一个基模型。

通过箱形图，我们可以看到硬投票方法对交叉验证整体预测结果分布带来的提升。

稍微修改一下上面的函数，我们对比硬投票和软投票的效果。

  1. def get_models():
  2.     models = dict()
  3.     models['knn1'] = KNeighborsClassifier(n_neighbors=1)
  4.     models['knn3'] = KNeighborsClassifier(n_neighbors=3)
  5.     models['knn5'] = KNeighborsClassifier(n_neighbors=5)
  6.     models['knn7'] = KNeighborsClassifier(n_neighbors=7)
  7.     models['knn9'] = KNeighborsClassifier(n_neighbors=9)
  8.     models['hard_voting'] = get_voting(voting='hard')
  9.     models['soft_voting'] = get_voting(voting='soft')
  10.     return models
  13. def get_voting(voting='hard'):
  14.     # define the base models
  15.     models = list()
  16.     models.append(('knn1', KNeighborsClassifier(n_neighbors=1)))
  17.     models.append(('knn3', KNeighborsClassifier(n_neighbors=3)))
  18.     models.append(('knn5', KNeighborsClassifier(n_neighbors=5)))
  19.     models.append(('knn7', KNeighborsClassifier(n_neighbors=7)))
  20.     models.append(('knn9', KNeighborsClassifier(n_neighbors=9)))
  21.     ensemble = VotingClassifier(estimators=models, voting=voting)
  23.     return ensemble
  1. X, y = get_dataset()
  2. models = get_models()
  3. results, names = list(), list()
  4. plt.figure(figsize=(4,8))
  5. for name, model in models.items():
  6.     scores = evaluate_model(model, X, y)
  7.     results.append(scores)
  8.     names.append(name)
  9.     print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores)))
  11. plt.boxplot(results, labels=names, showmeans=True)
  12. plt.show()

image.png

Refer

本笔记整理自DataWhale开源内容： https://github.com/datawhalechina/team-learning-data-mining/tree/master/EnsembleLearning