使用sklearn构建完整的机器学习项目流程
一般来说,一个完整的机器学习项目分为以下步骤:
1)明确项目任务:回归/分类
2)收集数据集并选择合适的特征。
3)选择度量模型性能的指标。
4)选择具体的模型并进行训练以优化模型。
5)评估模型的性能并调参。
1. 使用sklearn构建完整的回归项目
1.1 收集数据集并选择合适的特征
在数据集上我们使用我们比较熟悉的Boston房价数据集,原因是:
- 第一个,我们通过这些简单的数据集快速让我们上手sklearn,以及掌握sklearn的相关操作。
- 第二个,我们用简单的数据集能更加清晰地介绍机器学习的相关模型,避免在处理数据上花费较大的精力。
from sklearn import datasetsimport pandas as pdboston = datasets.load_boston()X = boston.datay = boston.targetfeatures = boston.feature_namesboston_data = pd.DataFrame(X,columns=features)boston_data["Price"] = yboston_data.head()
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT | Price | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.00632 | 18.0 | 2.31 | 0.0 | 0.538 | 6.575 | 65.2 | 4.0900 | 1.0 | 296.0 | 15.3 | 396.90 | 4.98 | 24.0 |
| 1 | 0.02731 | 0.0 | 7.07 | 0.0 | 0.469 | 6.421 | 78.9 | 4.9671 | 2.0 | 242.0 | 17.8 | 396.90 | 9.14 | 21.6 |
| 2 | 0.02729 | 0.0 | 7.07 | 0.0 | 0.469 | 7.185 | 61.1 | 4.9671 | 2.0 | 242.0 | 17.8 | 392.83 | 4.03 | 34.7 |
| 3 | 0.03237 | 0.0 | 2.18 | 0.0 | 0.458 | 6.998 | 45.8 | 6.0622 | 3.0 | 222.0 | 18.7 | 394.63 | 2.94 | 33.4 |
| 4 | 0.06905 | 0.0 | 2.18 | 0.0 | 0.458 | 7.147 | 54.2 | 6.0622 | 3.0 | 222.0 | 18.7 | 396.90 | 5.33 | 36.2 |
1.2 选择度量模型性能的指标
- MSE均方误差:
%20%3D%20%5Cfrac%7B1%7D%7Bn%5Ctext%7Bsamples%7D%7D%20%5Csum%7Bi%3D0%7D%5E%7Bn%5Ctext%7Bsamples%7D%20-%201%7D%20(y_i%20-%20%5Chat%7By%7D_i)%5E2.#card=math&code=%5Ctext%7BMSE%7D%28y%2C%20%5Chat%7By%7D%29%20%3D%20%5Cfrac%7B1%7D%7Bn%5Ctext%7Bsamples%7D%7D%20%5Csum%7Bi%3D0%7D%5E%7Bn%5Ctext%7Bsamples%7D%20-%201%7D%20%28y_i%20-%20%5Chat%7By%7D_i%29%5E2.)
- MAE平均绝对误差:
%20%3D%20%5Cfrac%7B1%7D%7Bn%7B%5Ctext%7Bsamples%7D%7D%7D%20%5Csum%7Bi%3D0%7D%5E%7Bn%7B%5Ctext%7Bsamples%7D%7D-1%7D%20%5Cleft%7C%20y_i%20-%20%5Chat%7By%7D_i%20%5Cright%7C#card=math&code=%5Ctext%7BMAE%7D%28y%2C%20%5Chat%7By%7D%29%20%3D%20%5Cfrac%7B1%7D%7Bn%7B%5Ctext%7Bsamples%7D%7D%7D%20%5Csum%7Bi%3D0%7D%5E%7Bn%7B%5Ctext%7Bsamples%7D%7D-1%7D%20%5Cleft%7C%20y_i%20-%20%5Chat%7By%7D_i%20%5Cright%7C)
决定系数:
%20%3D%201%20-%20%5Cfrac%7B%5Csum%7Bi%3D1%7D%5E%7Bn%7D%20(y_i%20-%20%5Chat%7By%7D_i)%5E2%7D%7B%5Csum%7Bi%3D1%7D%5E%7Bn%7D%20(yi%20-%20%5Cbar%7By%7D)%5E2%7D#card=math&code=R%5E2%28y%2C%20%5Chat%7By%7D%29%20%3D%201%20-%20%5Cfrac%7B%5Csum%7Bi%3D1%7D%5E%7Bn%7D%20%28yi%20-%20%5Chat%7By%7D_i%29%5E2%7D%7B%5Csum%7Bi%3D1%7D%5E%7Bn%7D%20%28y_i%20-%20%5Cbar%7By%7D%29%5E2%7D)
- 解释方差得分:
%20%3D%201%20-%20%5Cfrac%7BVar%5C%7B%20y%20-%20%5Chat%7By%7D%5C%7D%7D%7BVar%5C%7By%5C%7D%7D#card=math&code=explained%5C_%7B%7Dvariance%28y%2C%20%5Chat%7By%7D%29%20%3D%201%20-%20%5Cfrac%7BVar%5C%7B%20y%20-%20%5Chat%7By%7D%5C%7D%7D%7BVar%5C%7By%5C%7D%7D)
1.3 选择具体的模型并进行训练
线性回归模型
回归这个概念是19世纪80年代由英国统计学家郎西斯·高尔顿在研究父子身高关系提出来的,他发现:在同一族群中,子代的平均身高介于父代的身高以及族群的平均身高之间。具体而言,高个子父亲的儿子的身高有低于其父亲身高的趋势,而矮个子父亲的儿子身高则有高于父亲的身高的趋势。也就是说,子代的身高有向族群平均身高”平均”的趋势,这就是统计学上“回归”(“向平均回归”,regression to the mean)**的最初含义。
回归分析是一种预测性的建模技术,它研究的是因变量(目标)和自变量(特征)之间的关系。这种技术通常用于预测分析、时间序列模型以及发现变量之间的因果关系。通常使用曲线/线来拟合数据点,目标是使曲线到数据点的距离差异最小。而线性回归就是回归问题中的一种,线性回归假设目标值与特征之间线性相关,即满足一个多元一次方程。通过构建损失函数,来求解损失函数最小时的参数 :
假设:数据集%2C…%2C(x_N%2Cy_N)%20%5C%7D#card=math&code=D%20%3D%20%5C%7B%28x_1%2Cy_1%29%2C…%2C%28x_N%2Cy_N%29%20%5C%7D),
,
%5ET%2CY%3D(y_1%2Cy_2%2C…%2Cy_N)%5ET#card=math&code=X%20%3D%20%28x_1%2Cx_2%2C…%2Cx_N%29%5ET%2CY%3D%28y_1%2Cy_2%2C…%2Cy_N%29%5ET)
假设X和Y之间存在线性关系,模型的具体形式为%20%3Dw%5ETx#card=math&code=%5Chat%7By%7D%3Df%28w%29%20%3Dw%5ETx)
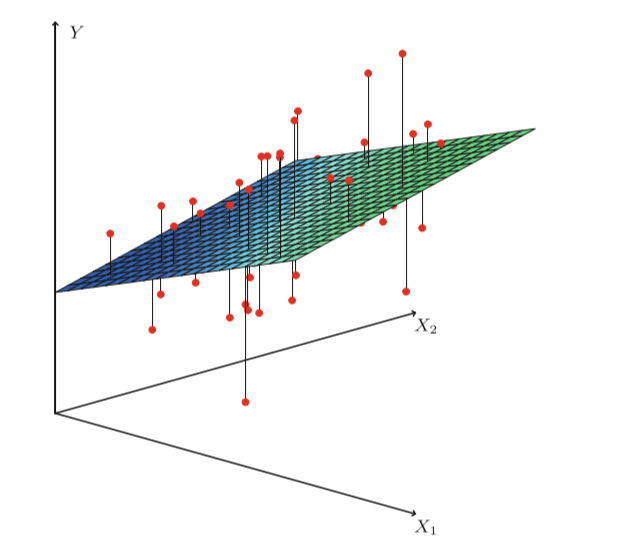
(a)损失函数
真实值 与线性回归模型的预测值
之间有一定的差距,我们定义一个函数来描述这个差距,这个函数称为损失函数。通过最小化损失函数来求解参数
。
求解思路有2种:一种是直接求解,叫标准方程法(Normal Equation,又叫正规方程法);另一种则是辗转求解,名为梯度下降法(gradient descent),又名最速下降法(steepest descent)。
求之不得,寤寐思服。悠哉悠哉,辗转反侧。
(b)最小二乘估计
最小二乘法是由勒让德在19世纪发现的,是一种在误差估计、不确定度、系统辨识及预测、预报等数据处理诸多学科领域得到广泛应用的数学工具。
在统计学中,高斯-马尔可夫定理(Gauss-Markov Theorem)陈述的是:在线性回归模型中,如果误差满足零均值、同方差且互不相关,则回归系数的最佳线性无偏估计(BLUE, Best Linear unbiased estimator)就是普通最小二乘法估计。
- 这里最佳的意思是指相较于其他估计量有更小方差的估计量,同时把对估计量的寻找限制在所有可能的线性无偏估计量中 。
- 值得注意的是这里不需要假定误差满足独立同分布(iid)或正态分布,而仅需要满足零均值、不相关及同方差这三个稍弱的条件 。
——百度百科—高斯马尔科夫定理
最小二乘法使用二范数的平方和 来描述真实值与回归模型预测值之间的差距,即:
因此,我们需要找到使得最小时对应的参数
,即:
为了达到求解最小化问题,我们应用高等数学的知识,使用求导来解决这个问题:
因此:
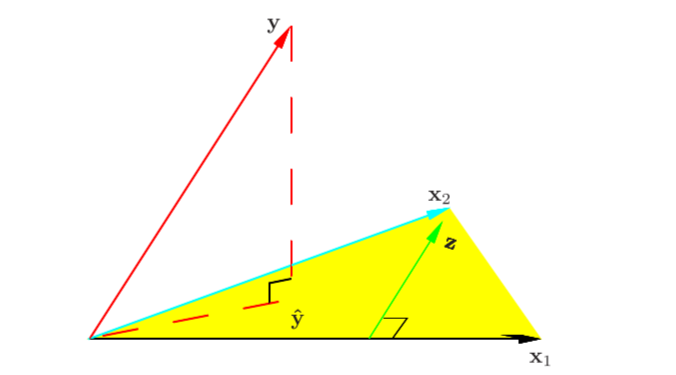
(c) 从几何解释角度看最小二乘法
最小二乘法中的几何意义是高维空间中的一个向量在低维子空间的投影
在线性代数中,我们知道两个向量a和b相互垂直可以得出:
而平面X的法向量为,与平面X互相垂直,因此:
即:
(d)从概率视角看最小二乘法**
最小二乘法(OLS)将问题转化成了一个凸优化问题。在线性回归中,它假设样本和噪声都服从高斯分布(为什么假设成高斯分布呢?其实这里隐藏了一个小知识点,就是中心极限定理,可以参考【central limit theorem】),最后通过极大似然估计(MLE)可以推导出最小二乘式子。
假设噪声%2Cy%3Df(w)%2B%5Cepsilon%3Dw%5ETx%2B%5Cepsilon#card=math&code=%5Cepsilon%20%5Cbacksim%20N%280%2C%5Csigma%5E2%29%2Cy%3Df%28w%29%2B%5Cepsilon%3Dw%5ETx%2B%5Cepsilon)
因此:#card=math&code=y%7Cxi%2Cw%20~%20N%28w%5ETx%2C%5Csigma%5E2%29)
我们使用极大似然估计MLE对参数w进行估计:

因此:线性回归的最小二乘估计<==>噪声的极大似然估计。
1.3.1 sklearn的线性回归实例
from sklearn import linear_model # 引入线性回归方法lin_reg = linear_model.LinearRegression() # 创建线性回归的类lin_reg.fit(X,y) # 输入特征X和因变量y进行训练print("模型系数:",lin_reg.coef_) # 输出模型的系数print("模型得分:",lin_reg.score(X,y)) # 输出模型的决定系数R^2
输出:
模型系数: [-1.08011358e-01 4.64204584e-02 2.05586264e-02 2.68673382e+00 -1.77666112e+01 3.80986521e+00 6.92224640e-04 -1.47556685e+00 3.06049479e-01 -1.23345939e-02 -9.52747232e-01 9.31168327e-03 -5.24758378e-01] 模型得分: 0.7406426641094095
1.3.2 线性回归的推广
在线性回归中,我们假设因变量与特征之间的关系是线性关系,这样的假设使得模型很简单,但是缺点也是显然的,那就是当数据存在非线性关系时,我们使用线性回归模型进行预测会导致预测性能极其低下,因为模型的形式本身是线性的,无法表达数据中的非线性关系。我们一个很自然的想法就是去推广线性回归模型,使得推广后的模型更能表达非线性的关系。
(1)多项式回归
为了体现因变量和特征的非线性关系,一个很自然而然的想法就是将标准的线性回归模型:
换成一个多项式函数:
对于多项式的阶数d不能取过大,一般不大于3或者4,因为d越大,多项式曲线就会越光滑,在X的边界处有异常的波动。(图中的边界处的4阶多项式拟合曲线的置信区间(虚线表示置信区间)明显增大,预测效果的稳定性下降。)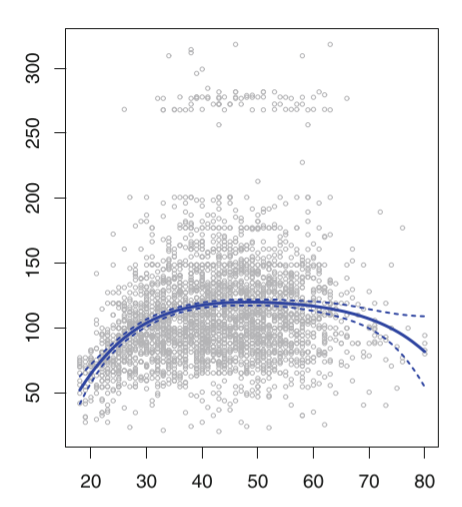
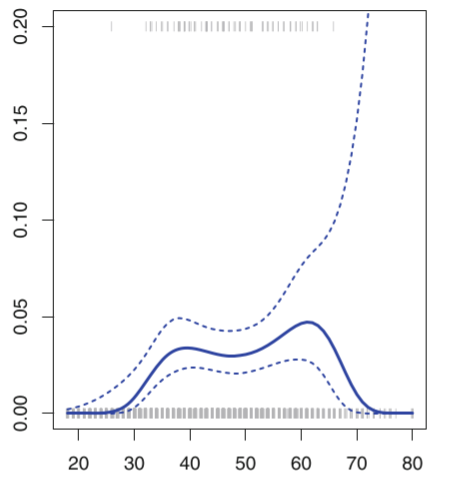
(2)广义可加模型(GAM)
广义可加模型GAM实际上是线性模型推广至非线性模型的一个框架,在这个框架中,每一个变量都用一个非线性函数来代替,但是模型本身保持整体可加性。GAM模型不仅仅可以用在线性回归的推广,还可以将线性分类模型进行推广。具体的推广形式是:
标准的线性回归模型:
GAM模型框架:
GAM模型的优点与不足:
- 优点:简单容易操作,能够很自然地推广线性回归模型至非线性模型,使得模型的预测精度有所上升;由于模型本身是可加的,因此GAM还是能像线性回归模型一样把其他因素控制不变的情况下单独对某个变量进行推断,极大地保留了线性回归的易于推断的性质。
- 缺点:GAM模型会经常忽略一些有意义的交互作用,比如某两个特征共同影响因变量,不过GAM还是能像线性回归一样加入交互项
的形式进行建模;但是GAM模型本质上还是一个可加模型,如果我们能摆脱可加性模型形式,可能还会提升模型预测精度,详情请看后面的算法。
(3)多项式回归实例介绍
sklearn.preprocessing.PolynomialFeatures(degree=2, *, interaction_only=False, include_bias=True, order=’C’):
参数:
- degree:特征转换的阶数。
- interaction_onlyboolean:是否只包含交互项,默认False 。
- include_bias:是否包含截距项,默认True。
- order:str in {‘C’, ‘F’}, default ‘C’,输出数组的顺序。
from sklearn.preprocessing import PolynomialFeaturesimport numpy as npX_arr = np.arange(6).reshape(3, 2)print("原始X为:\n",X_arr)poly = PolynomialFeatures(2)print("2次转化X:\n",poly.fit_transform(X_arr))poly = PolynomialFeatures(interaction_only=True)print("2次转化X:\n",poly.fit_transform(X_arr))
原始X为: [[0 1] [2 3] [4 5]] 2次转化X: [[ 1. 0. 1. 0. 0. 1.] [ 1. 2. 3. 4. 6. 9.] [ 1. 4. 5. 16. 20. 25.]] 2次转化X: [[ 1. 0. 1. 0.] [ 1. 2. 3. 6.] [ 1. 4. 5. 20.]]
(4)GAM模型实例介绍
需要先安装pygam:pip install pygam
https://github.com/dswah/pyGAM/blob/master/doc/source/notebooks/quick_start.ipynb
from pygam import LinearGAMgam = LinearGAM().fit(boston_data[boston.feature_names], y)gam.summary()
LinearGAM
=============================================== ========================================================== Distribution: NormalDist Effective DoF: 103.2423 Link Function: IdentityLink Log Likelihood: -1589.7653 Number of Samples: 506 AIC: 3388.0152 AICc: 3442.7649 GCV: 13.7683 Scale: 8.8269
Pseudo R-Squared: 0.9168========================================================================================================== Feature Function Lambda Rank EDoF P > x Sig. Code
================================= ==================== ============ ============ ============ ============ s(0) [0.6] 20 11.2 2.20e-11 *
s(1) [0.6] 20 12.8 8.15e-02 .
s(2) [0.6] 20 13.5 2.59e-03
s(3) [0.6] 20 3.7 2.76e-01
s(4) [0.6] 20 11.4 1.11e-16
s(5) [0.6] 20 10.2 1.11e-16
s(6) [0.6] 20 10.4 8.22e-01
s(7) [0.6] 20 8.5 4.44e-16 *
s(8) [0.6] 20 3.6 5.96e-03
s(9) [0.6] 20 3.3 1.33e-09 *
s(10) [0.6] 20 1.8 3.26e-03
s(11) [0.6] 20 6.4 6.25e-02 .
s(12) [0.6] 20 6.5 1.11e-16 *intercept 1 0.0 2.23e-13 *
Significance codes: 0 ‘*’ 0.001 ‘‘ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1 WARNING: Fitting splines and a linear function to a feature introduces a model identifiability problem which can cause p-values to appear significant when they are not. WARNING: p-values calculated in this manner behave correctly for un-penalized models or models with
known smoothing parameters, but when smoothing parameters have been estimated, the p-values are typically lower than they should be, meaning that the tests reject the null too readily.
1.3.3 回归树
基于树的回归方法主要是依据分层和分割的方式将特征空间划分为一系列简单的区域。对某个给定的待预测的自变量,用他所属区域中训练集的平均数或者众数对其进行预测。由于划分特征空间的分裂规则可以用树的形式进行概括,因此这类方法称为决策树方法。
决策树由结点(node)和有向边(diredcted edge)组成。结点有两种类型:内部结点(internal node)和叶结点(leaf node)。内部结点表示一个特征或属性,叶结点表示一个类别或者某个值。区域 𝑅1,𝑅2 等称为叶节点,将特征空间分开的点为内部节点。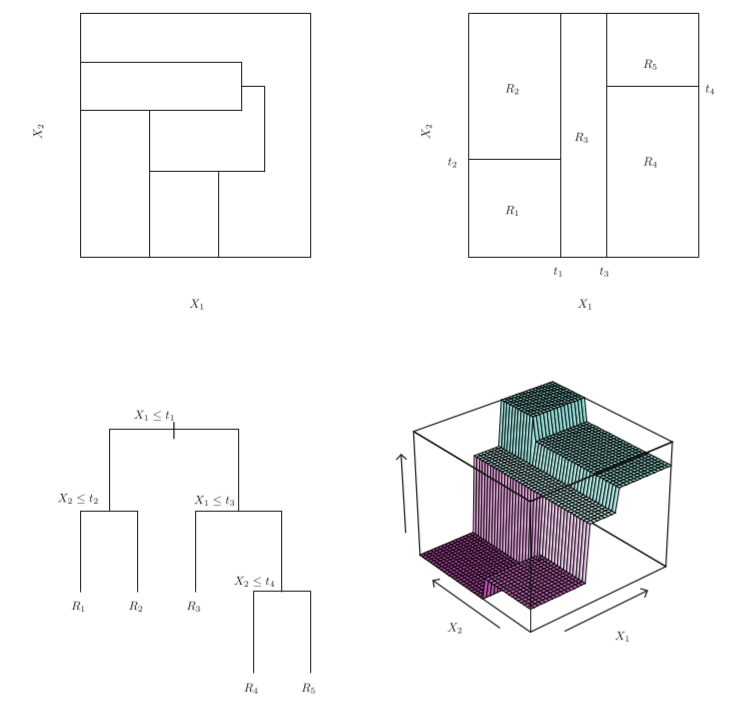
1.3.3.1 建立回归树:
建立回归树的过程大致可以分为以下两步:
- 将自变量的特征空间(即
)的可能取值构成的集合分割成 J 个互不重叠的区域
。
- 对落入区域
的每个观测值作相同的预测,预测值等于
上训练集的因变量的简单算术平均。
具体来说,就是:
a. 选择最优切分特征j以及该特征上的最优点s:
遍历特征j以及固定j后遍历切分点s,选择使得下式最小的(j,s)
b. 按照(j,s)分裂特征空间:
和
c. 继续调用步骤1,2直到满足停止条件,就是每个区域的样本数小于等于5。
d. 将特征空间划分为 J 个不同的区域,生成回归树:
如以下生成的关于运动员在棒球大联盟数据的回归树: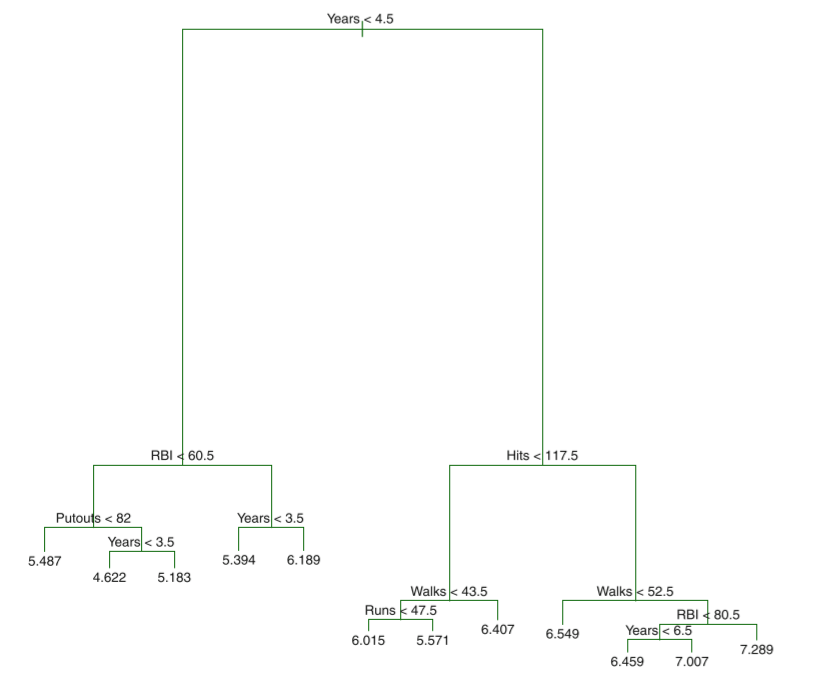
1.3.3.2 回归树与线性模型的比较:
线性模型的模型形式与树模型的模型形式有着本质的区别,具体而言,线性回归对模型形式做了如下假定: ,而回归树则是
。那问题来了,哪种模型更优呢?这个要视具体情况而言,如果特征变量与因变量的关系能很好的用线性关系来表达,那么线性回归通常有着不错的预测效果,拟合效果则优于不能揭示线性结构的回归树。反之,如果特征变量与因变量的关系呈现高度复杂的非线性,那么树方法比传统方法更优。
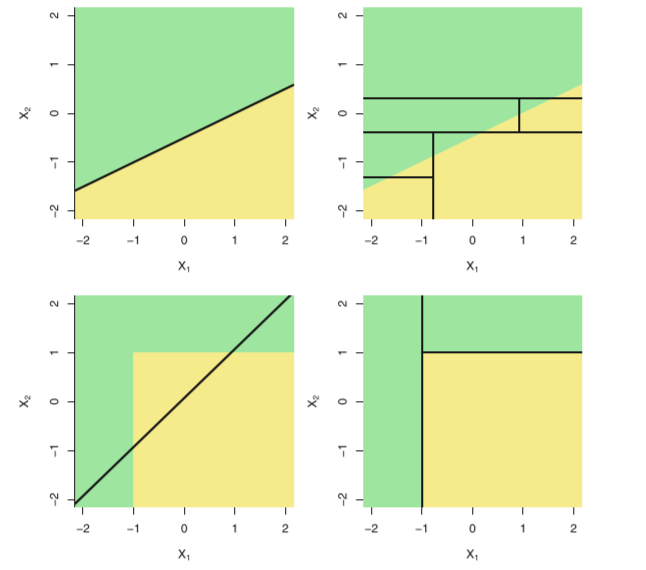
1.3.3.3 树模型的优缺点:
- 树模型的解释性强,在解释性方面可能比线性回归还要方便。
- 树模型更接近人的决策方式。
- 树模型可以用图来表示,非专业人士也可以轻松解读。
- 树模型可以直接做定性的特征而不需要像线性回归一样哑元化。(可以直接处理分类变量,不需要one-hot编码)
- 树模型能很好处理缺失值和异常值,对异常值不敏感,但是这个对线性模型来说却是致命的。
- 树模型的预测准确性一般无法达到其他回归模型的水平,但是改进的方法很多。
1.3.3.4 sklearn使用回归树的实例:
sklearn.tree.DecisionTreeRegressor(*, criterion=’mse’, splitter=’best’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, presort=’deprecated’, ccp_alpha=0.0)
常用参数:
- criterion:{“ mse”,“ friedman_mse”,“ mae”},默认=“ mse”。衡量分割标准的函数 。
- splitter:{“best”, “random”}, default=”best”。分割方式。
- max_depth:树的最大深度。
- min_samples_split:拆分内部节点所需的最少样本数,默认是2。
- min_samples_leaf:在叶节点处需要的最小样本数。默认是1。
- min_weight_fraction_leaf:在所有叶节点处(所有输入样本)的权重总和中的最小加权分数。如果未提供sample_weight,则样本的权重相等。默认是0。
from sklearn.tree import DecisionTreeRegressor
reg_tree = DecisionTreeRegressor(criterion = "mse",min_samples_leaf = 5)
reg_tree.fit(X,y)
reg_tree.score(X,y)
0.9376307599929274
1.3.4 支持向量机回归(SVR)
在介绍支持向量回归SVR之前,我们先来了解下约束优化的相关知识:
1.3.4.1 约束优化问题(P)
约束最优化问题(constrained optimization problem)是指具有约束条件的非线性规划问题。仅有等式约束条件的约束最优化问题,可采用消元法、拉格朗日乘子法或罚函数法,将其化为无约束最优化问题求解;对于含有等式约束和不等式约束条件的最优化问题,可采用以下方法:将不等式约束化为等式约束;将约束问题化为无约束问题;将非线性规划问题用线性逼近的方法来近似求解;在可行域中沿某方向作一维搜索,寻求最优解 。
—— 百度百科—约束最优化问题
我们假设 为满足以上条件的局部最优解,
,我们的目的就是要找到
与
,满足不等式和等式约束的x集合成为可行域,记作S。
- KKT条件(Karush–Kuhn–Tucker conditions,最优解的一阶必要条件)
因为KKT条件是最优化的相关内容,在本次开源学习中并不是重点,因此在这里我用一个更加简单的例子说明KKT条件,严格的证明请参见凸优化相关书籍。
在这个例子中,我们考虑:( 为我们的最优解)
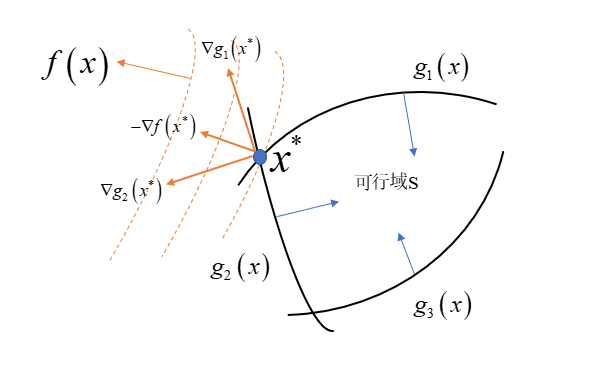
我们可以看到: 可以由
与
线性表示,因此有:
,其中
,即:
,其中
我们把没有起作用的约束也放到式子里面去,目的也就是为了书写方便,即要求:
,其中
由于点 位于方程
与
上,因此:
因此,KKT条件就是:假设 为最优化问题(P)的局部最优解,且
在某个适当的条件下 ,有:
(对偶条件)
(对偶条件)
(原问题条件)
(原问题条件)
(互补松弛定理)
- 对偶理论:
对偶理论是研究线性规划中原始问题与对偶问题之间关系的理论。 在线性规划早期发展中最重要的发现是对偶问题,即每一个线性规划问题(称为原始问题)有一个与它对应的对偶线性规划问题(称为对偶问题)。 1928年美籍匈牙利数学家 J.von诺伊曼在研究对策论发现线性规划与对策论之间存在着密切的联系。两零和对策可表达成线性规划的原始问题和对偶问题。 ——百度百科—对偶理论
对偶是大自然中广泛存在的,呈“分形”形态分布的一种结构规律,及任何系统往下和往上均可找出对偶二象的结构关系,且二象间具有完全性、互补性、对立统一性、稳定性、互涨性和互根性。 对偶问题:每一个线性规划问题都存在一个与其对偶的问题,原问题与对偶问题对一个实际问题从不同角度提出来,并进行描述,组成一对互为对偶的线性规划问题。
对偶空间:设V为数域P上一个n 维线性空间。V上全体线性函数组成的集合记作L(V,P)。定义在L(V,P)上的加法和数量乘法:(f+g)(a)=f(a)+g(a),(kf)(a)=kf(a),则L(V,P)也是数域P上的线性空间。这样构造的L(V,P)就称为V的对偶空间。
——百度百科—对偶 (数学术语)
为什么要引入对偶问题呢?是因为原问题与对偶问题就像是一个问题两个角度去看,如利润最大与成本最低等。有时侯原问题上难以解决,但是在对偶问题上就会变得很简单。再者,任何一个原问题在变成对偶问题后都会变成一个凸优化的问题,这点我们后面会有介绍。下面我们来引入对偶问题:
首先,我们的原问题(P)是:
引入拉格朗日函数:
拉格朗日对偶函数:,其中𝑋为满足条件的𝑥变量
,由于
,其中𝑆为可行域
因此:拉格朗日对偶函数是原问题最优解的函数值
的下界,即每个不同的
与
确定的
都是
的下界,但是我们希望下界越大越好,因为越大就更能接近真实的
。因此:
拉格朗日对偶问题(D)转化为:
也就是:
我们可以观察到,对偶问题是关于和
的线性函数,因此对偶问题是一个凸优化问题,凸优化问题在最优化理论较为简单。
弱对偶定理:对偶问题(D)的最优解 一定小于原问题最优解
,这点在刚刚的讨论得到了充分的证明,一定成立。
强对偶定理:对偶问题(D)的最优解 在一定的条件下等于原问题最优解
,条件非常多样化且不是唯一的,也就是说这是个开放性的问题,在这里我给出一个最简单的条件,即:
与
为凸函数,
为线性函数,X是凸集,
满足KKT条件,那么
。
1.3.4.2 支持向量回归SVR
在介绍完了相关的优化知识以后,我们开始正式学习支持向量回归SVR。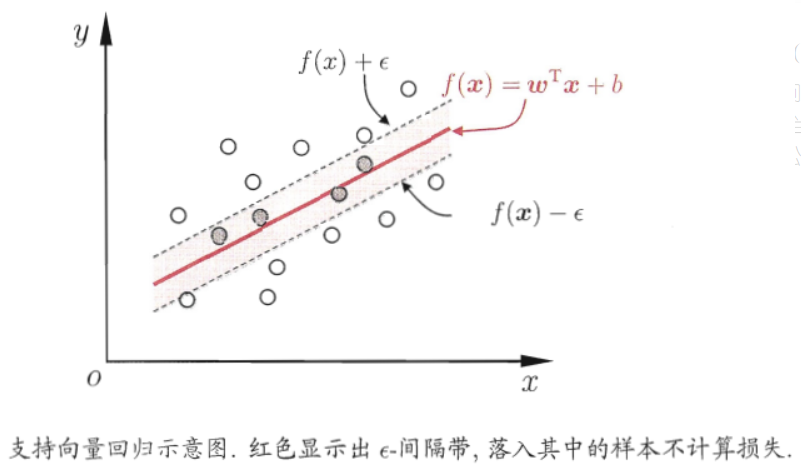
在线性回归的理论中,每个样本点都要计算平方损失,但是SVR却是不一样的。SVR认为:落在 𝑓(𝑥) 的 𝜖 邻域空间中的样本点不需要计算损失,这些都是预测正确的,其余的落在 𝜖 邻域空间以外的样本才需要计算损失,因此: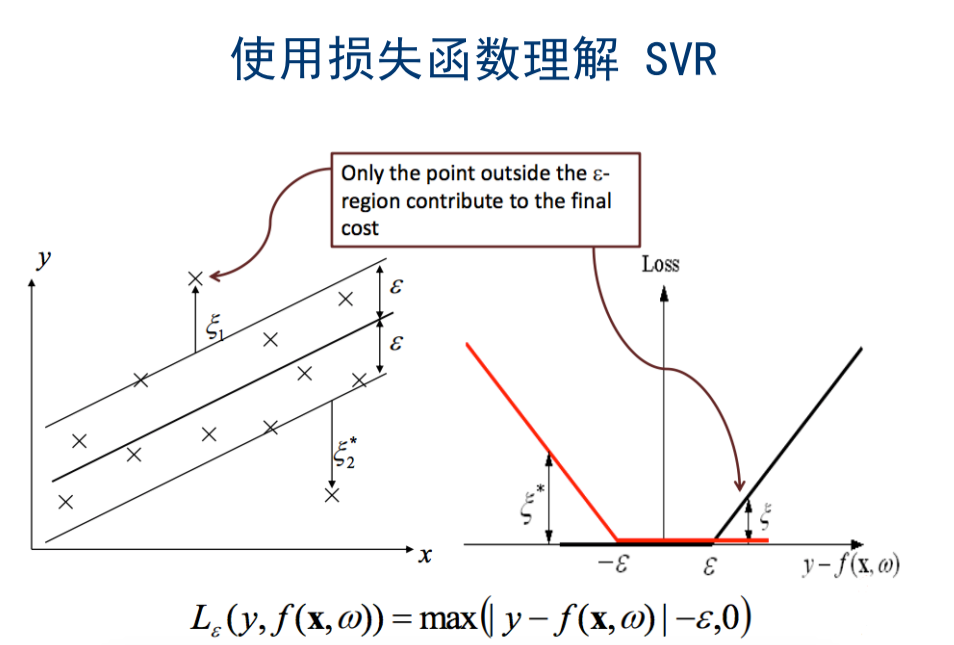
引入拉格朗日函数:
再令 对
求偏导等于0,得:
。
上述过程中需满足KKT条件,即要求:
SVR的解形如:
1.3.4.3 sklearn中使用SVR实例
参考API文档: https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVR.html?highlight=svr#sklearn.svm.SVR
sklearn.svm.SVR(*, kernel=’rbf’, degree=3, gamma=’scale’, coef0=0.0, tol=0.001, C=1.0, epsilon=0.1, shrinking=True, cache_size=200, verbose=False, max_iter=-1)
常用参数:
- kernel:核函数,{‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’}, 默认=’rbf’。(后面会详细介绍)
- degree:多项式核函数的阶数。默认 = 3。
- C:正则化参数,默认=1.0。(后面会详细介绍)
- epsilon:SVR模型允许的不计算误差的邻域大小。默认0.1。 ```python from sklearn.svm import SVR from sklearn.preprocessing import StandardScaler # 标准化数据 from sklearn.pipeline import make_pipeline # 使用管道,把预处理和模型形成一个流程
reg_svr = make_pipeline(StandardScaler(), SVR(C=1.0, epsilon=0.2)) reg_svr.fit(X, y) reg_svr.score(X,y) ```
0.7024525421955279

