解决思路

双指针-滑动窗口

大量的重复计算
即如果我们已经知道nums[i….j]的和，那么就可以很快地知道nums[i….j-1]的和，而不用重复计算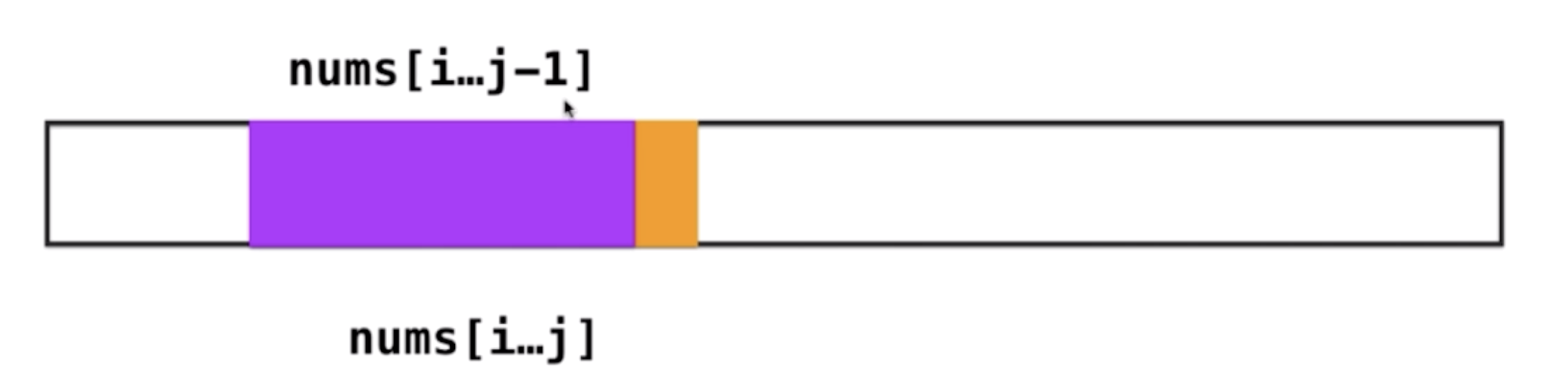

滑动窗口

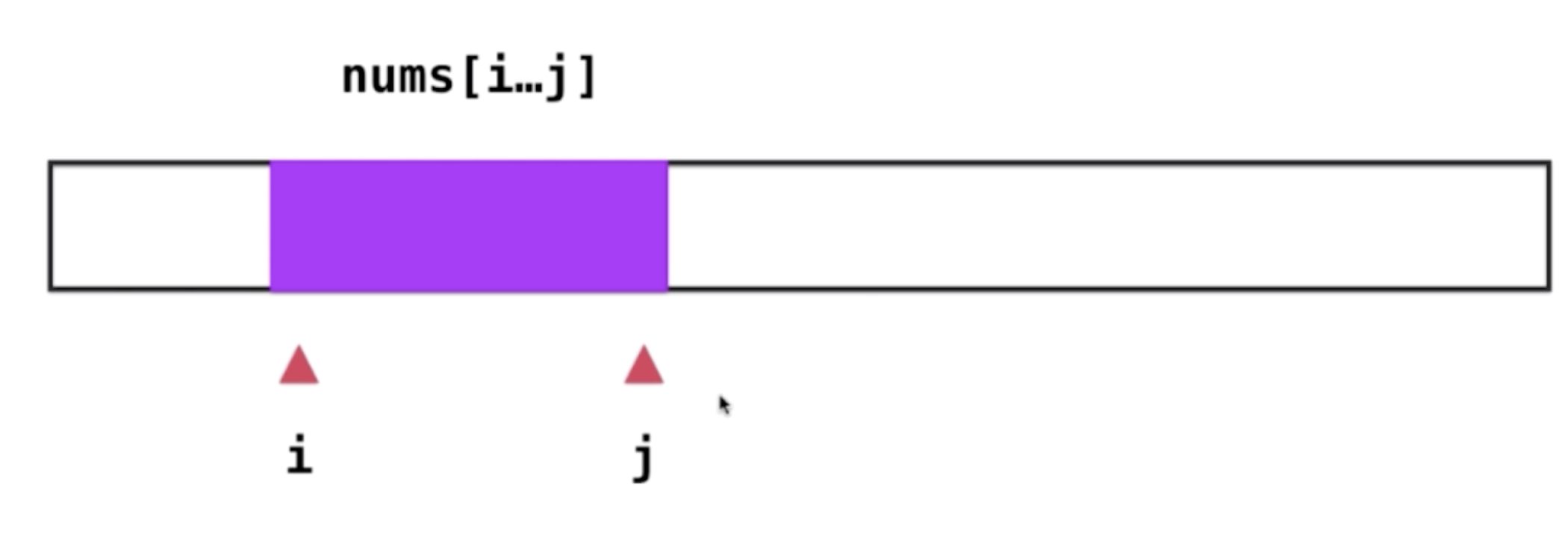
1. 对于当前的子数组，如果和不到s,则向后多看一个数

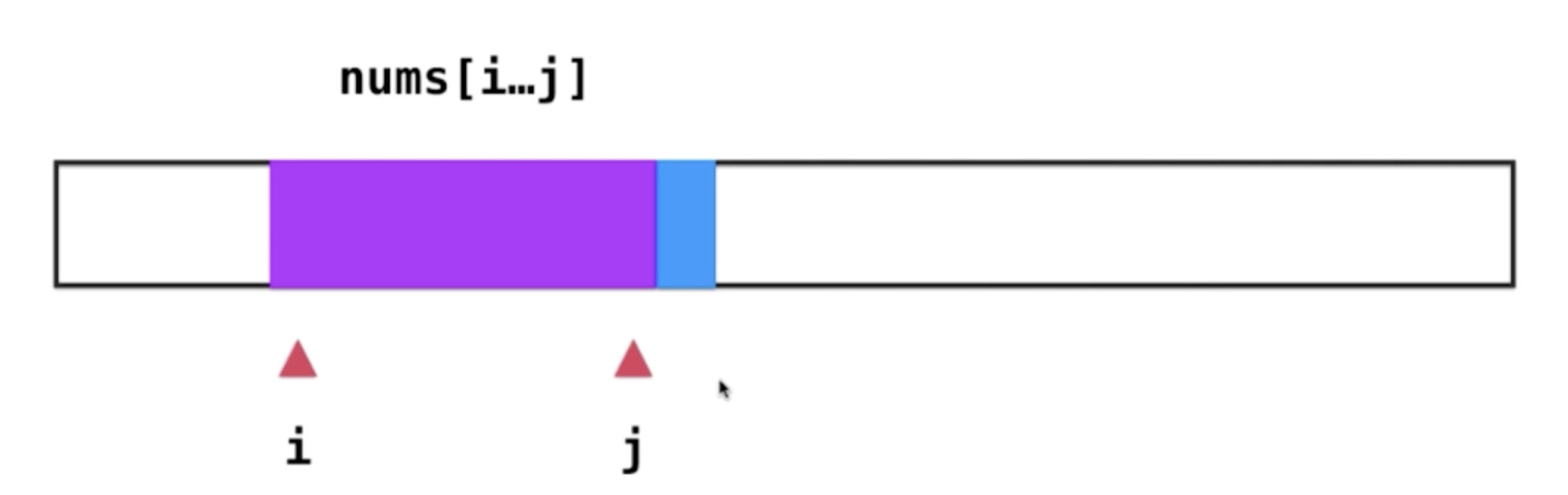
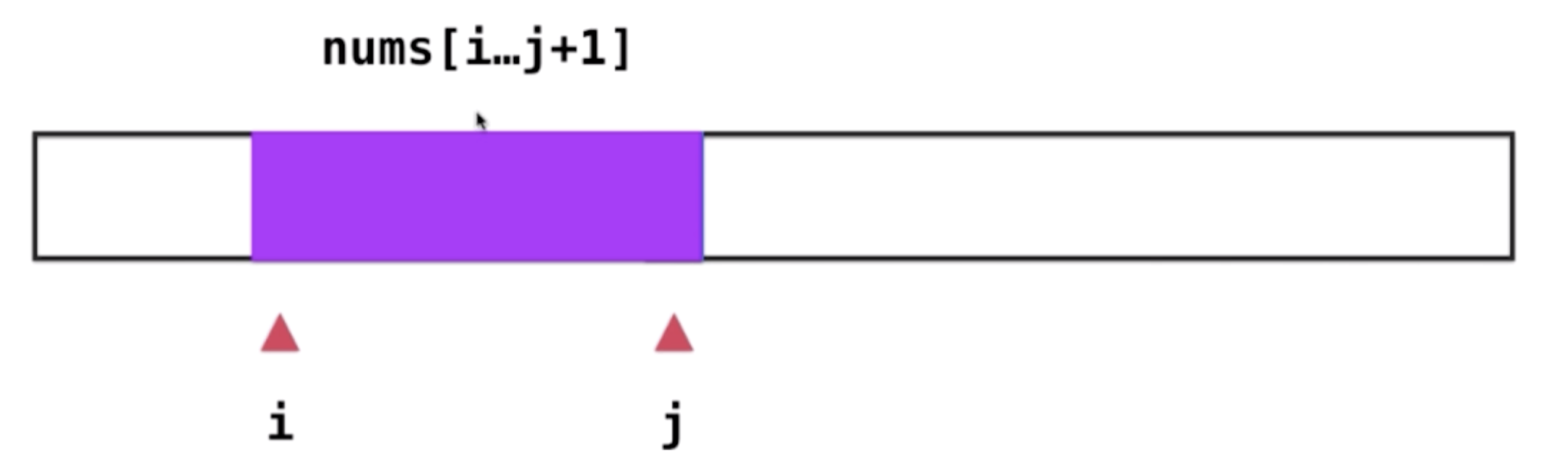
1. 看nums[i,….,j+1]的数组的和的大小，如果找到大于s的sum，则记录最小值

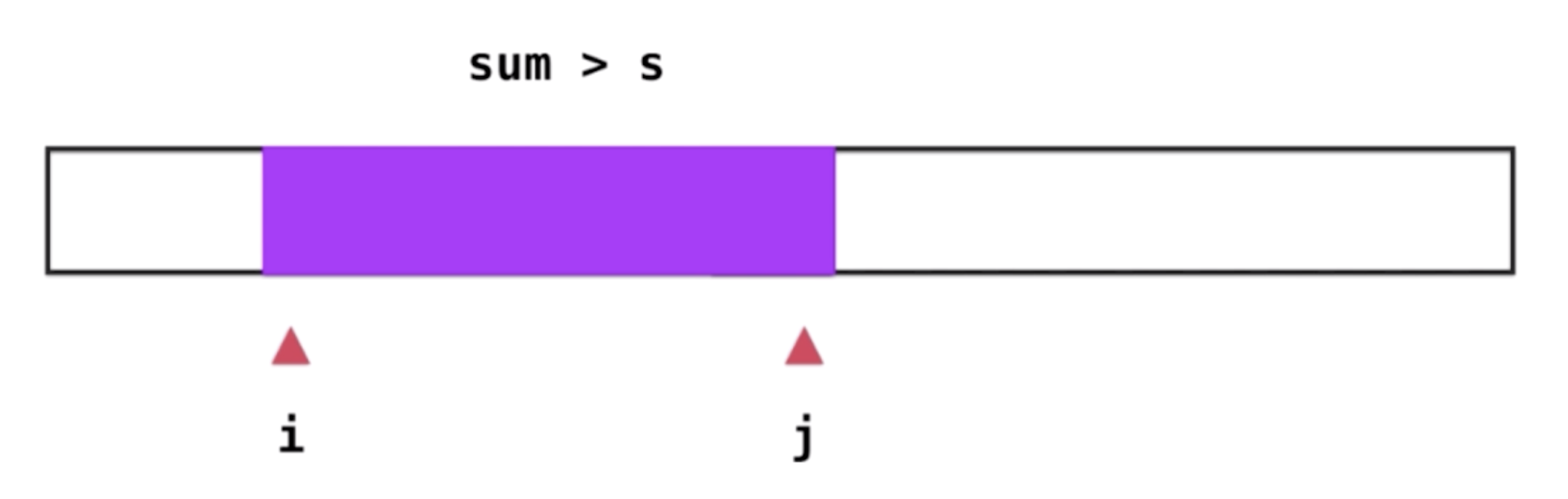
1. 此时从i端缩小连续子数组，让i—，此时sum就会变小，一直到sum的和小于s

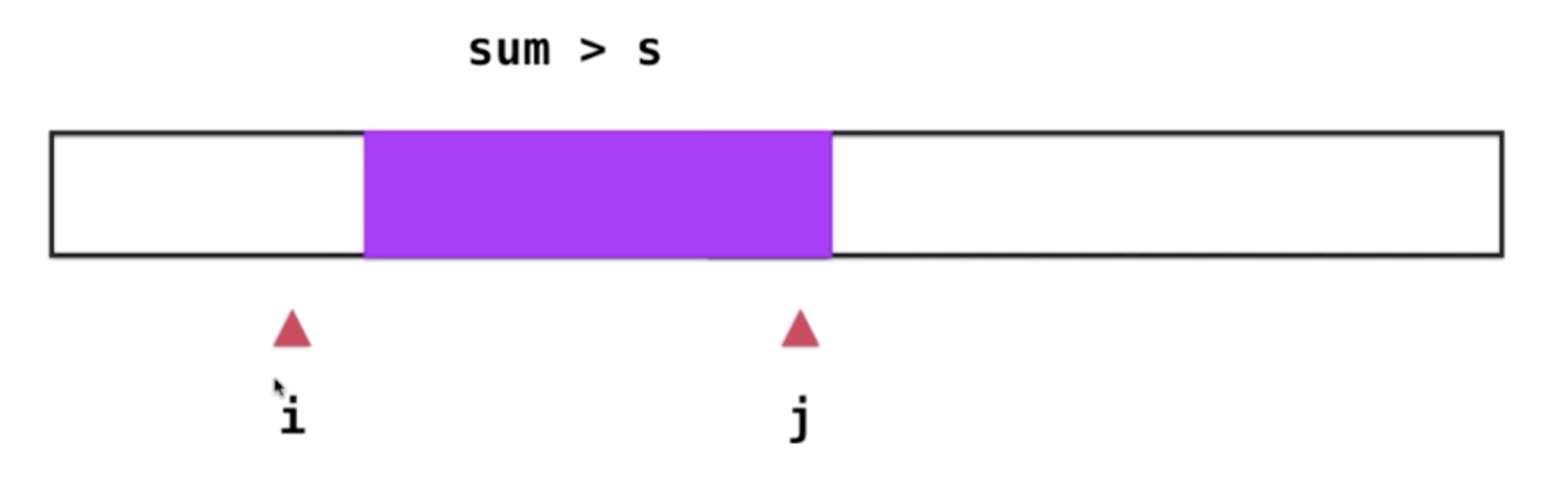
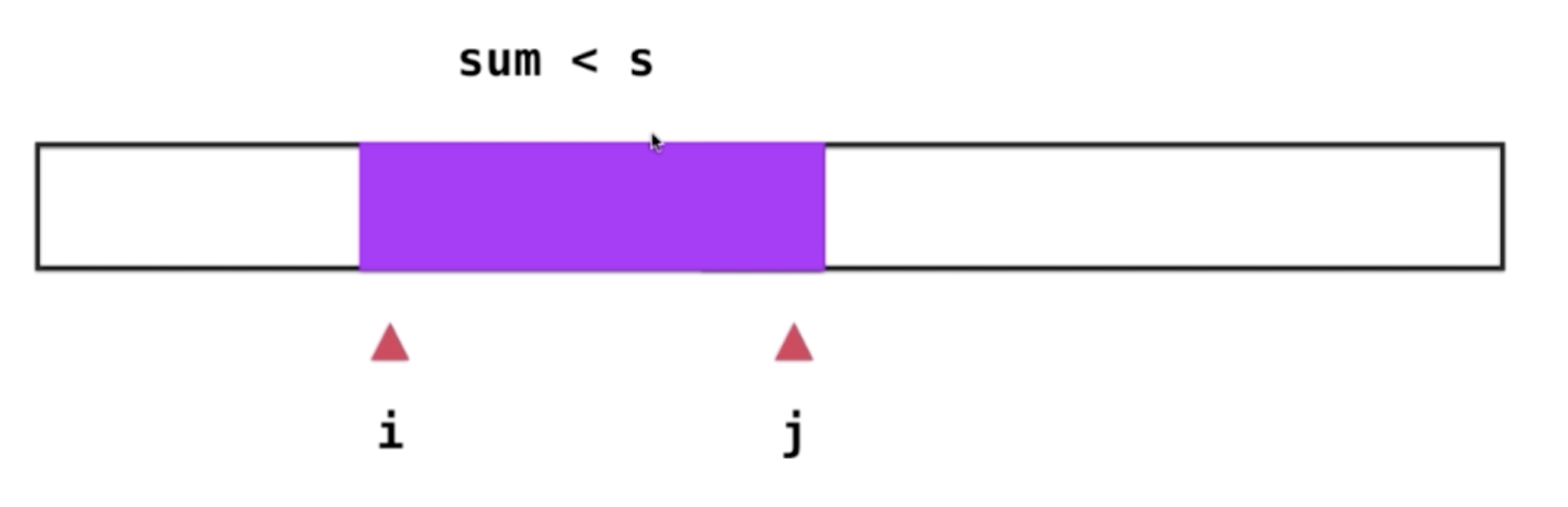
1. 此时j指针继续向前前进，一直到sum的值大于s.依次类推

在整个过程中一直保持一个窗口，该窗口被i和j两个索引所圈定的。该窗口不停地向前滑动来寻找满足题意的数组，即为滑动窗口

public int minSubArrayLen(int s, int[] nums) {
        //nums[l,....,r]即为滑动窗口 
        //初始r为-1即表示最开始滑动窗口中不包含任何元素
        int l=0,r=-1;
        //res记录最小的连续子数组的长度 这里res初始取nums.length+1表示当前取不到的值
        int res = nums.length+1;
        //窗口中元素的和
        int sum = 0;
        //如果l到达了边界 表示没有取值
        while(l<nums.length){
            //如果sum<s 右边界++ 和累加 此时需要判断数组下标
            if(r+1<nums.length && sum<s)
            {
                //右边界++
                r++;
                sum += nums[r];
            }
            //如果sum>=s  和去掉左边界 左边界++
            else{
                sum -= nums[l];
                l++;
            } 
            //如果和大于s 记录res 需要注意【】前闭后闭 应该r-l+1
            if(sum>=s){
                res = res>r-l+1?r-l+1:res;
            }
        }
        //如果res没有被更新 则没有解
        if(res == nums.length+1)
            return 0;
        return res;
    }
//time O(n) 
//space O(1)