解题思路

递归

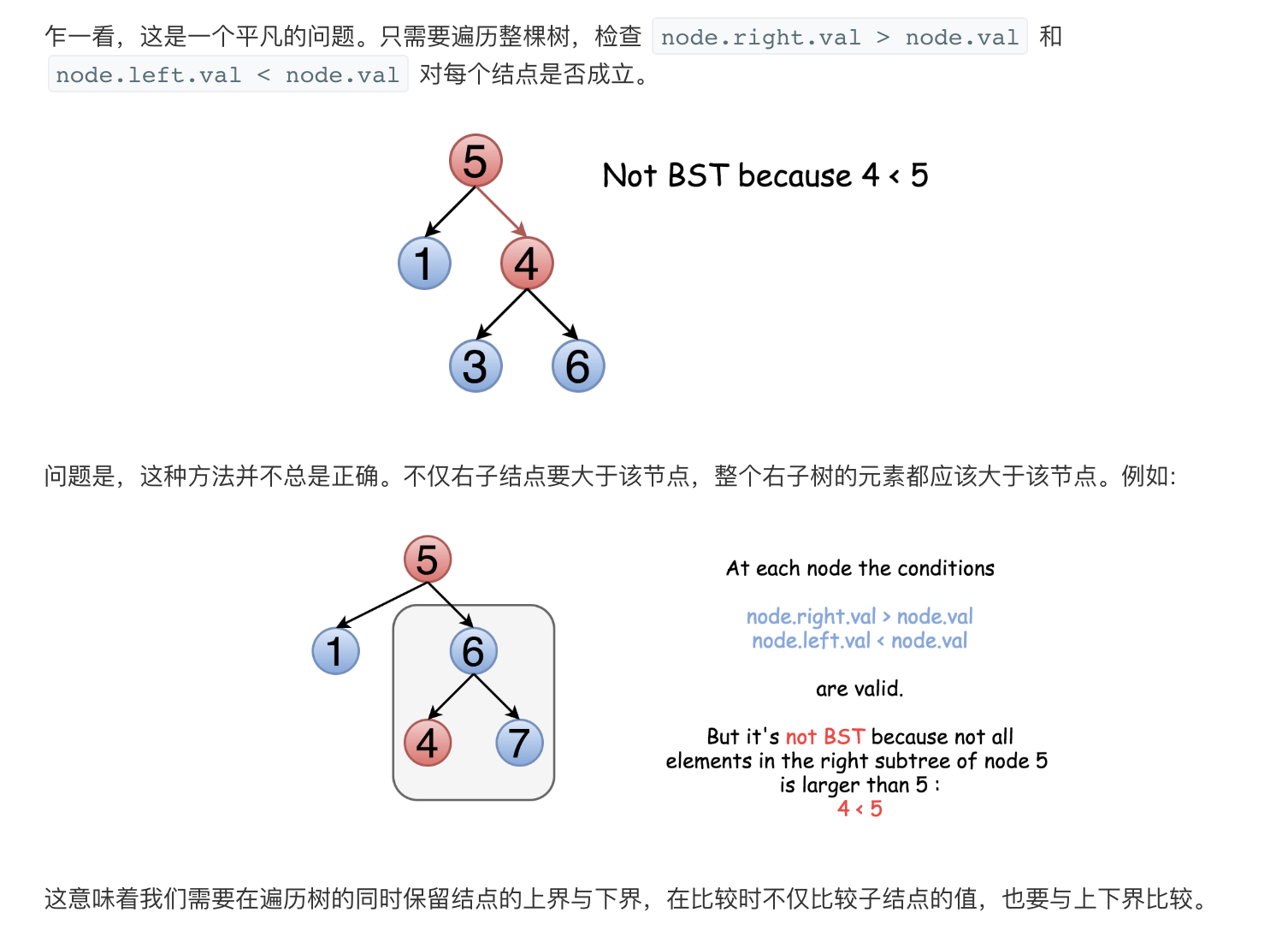
上述思路可以用递归法实现。首先将结点的值与上界和下界（如果有）比较。然后，对左子树和右子树递归进行该过程。

     public boolean isValidBST(TreeNode root){
        return helper(root,null,null);
    }
    public boolean helper(TreeNode node,Integer lower,Integer upper){
        if(node==null) return true;
        int val = node.val;
        //判断上下界
        if(lower!=null&&val<=lower) return false;
        if(upper!=null&&val>=upper) return false;
        //递归将值带入判断上下界
        if(!helper(node.left,lower,val)) return false;
        if(!helper(node.right,val,upper)) return false;
        return true;
    }

中序遍历

我们使用
中序遍历
左子树 -> 结点 -> 右子树的顺序。

上面的结点按照访问的顺序标号，你可以按照 1-2-3-4-5 的顺序来比较不同的策略。

左子树 -> 结点 -> 右子树 意味着对于二叉搜索树而言，每个元素都应该比下一个元素小。

因此，具有 {O}(N) 时间复杂度与 {O}(N) 空间复杂度的算法十分简单: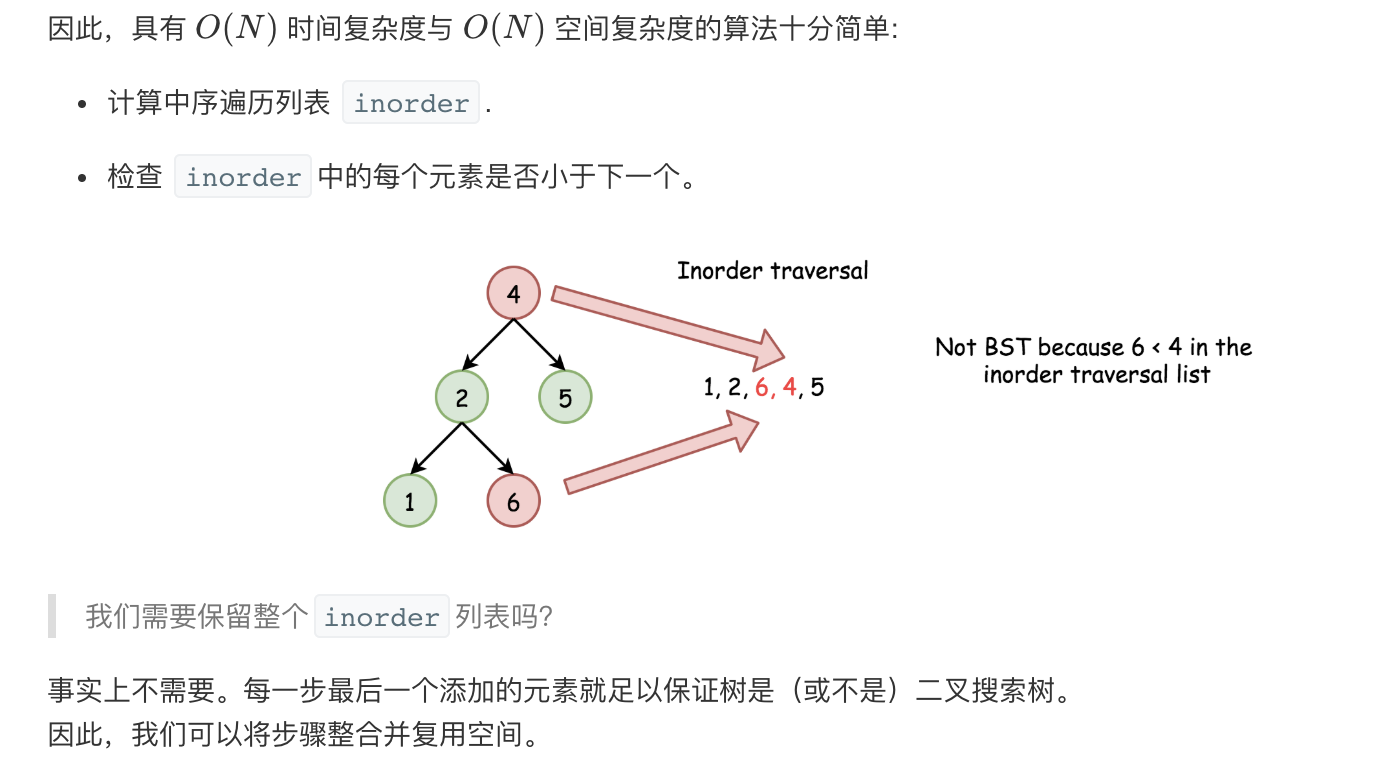

 public boolean isValidBST(TreeNode root){
        Stack<TreeNode> stack = new Stack<>();
        double inorder = - Double.MAX_VALUE;
        while(!stack.isEmpty()||root!=null){
            while(root!=null){
                stack.push(root);
                root=root.left;
            }
            root = stack.pop();
            if(root.val<=inorder) return false;
            inorder = root.val;
            root = root.right;
        }
        return true;
    }