343. 整数拆分

思路

以分割4获得最大乘积为例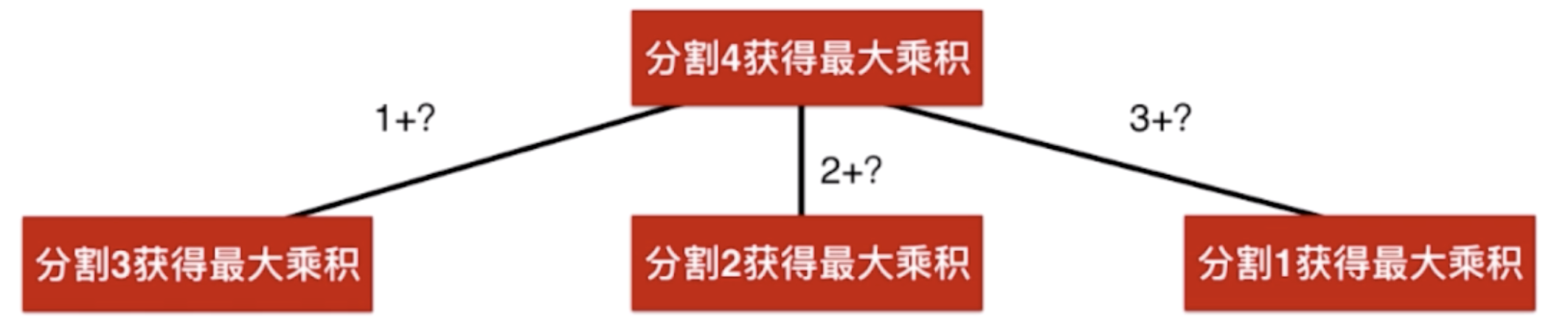

求得分割3的最大乘积后再乘以1即为1种备选答案，求得分割2的最大乘积后再乘以2也是1种备选答案，求得分割1的最大乘积后再乘以3也是1种备选答案。将这三种答案进行组合就是分割4获得的最大乘积

因此将其转换为3个子问题

同理对于分割3而言，可以进一步地写为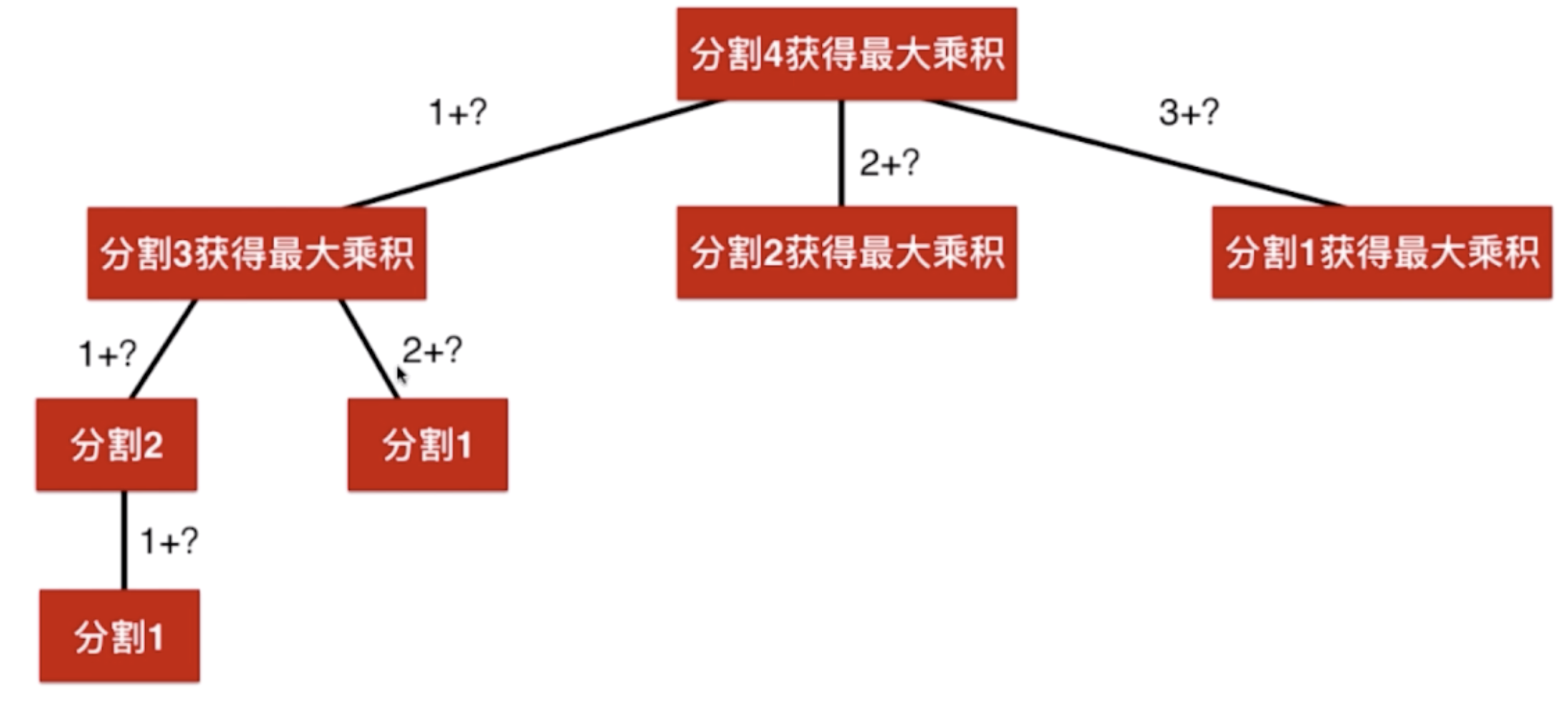

因此总体的分割形式为，这样就得到了所有的解，所有也就知道了分割4的最大乘积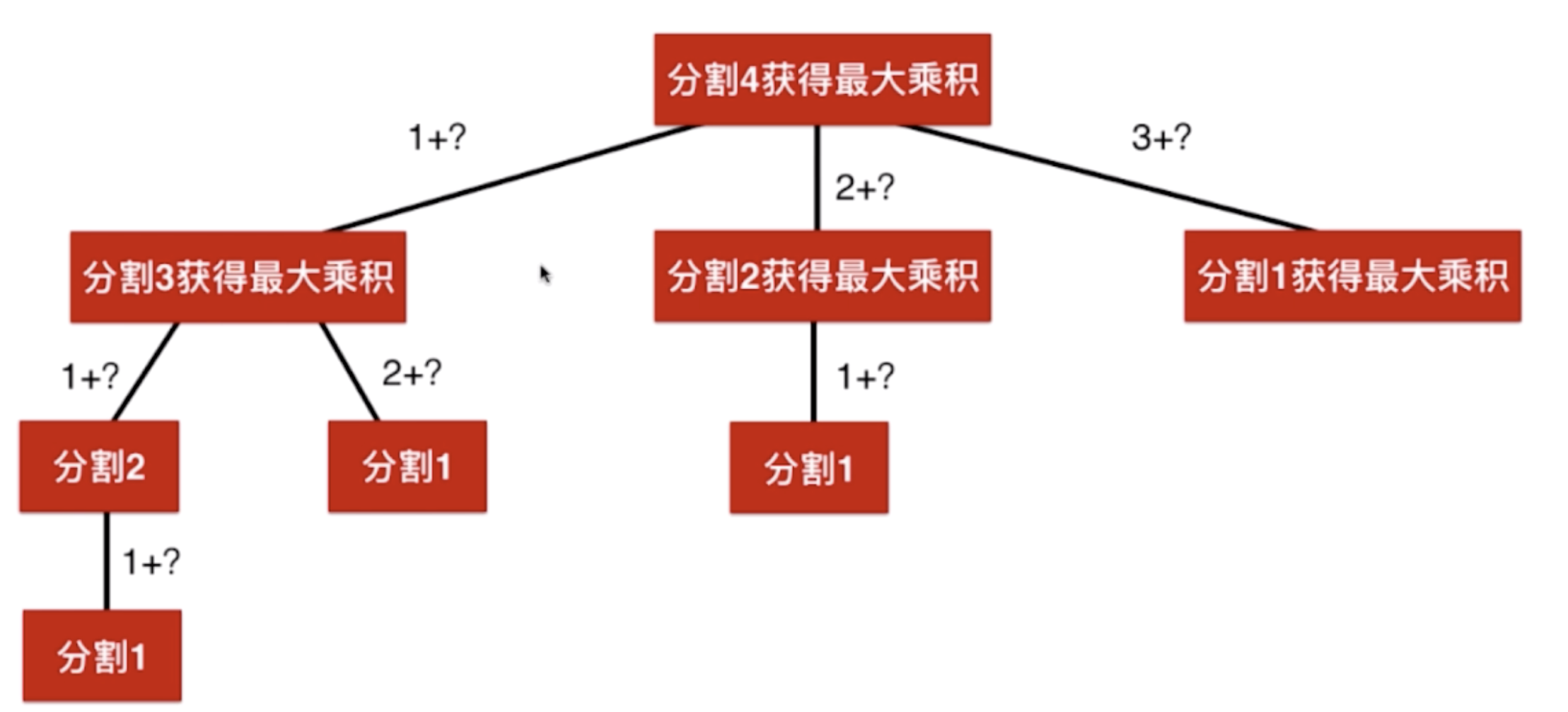

显然这里有重叠的子问题，例如分割2计算了两次，所以可以使用记忆话搜索或动态规划来求解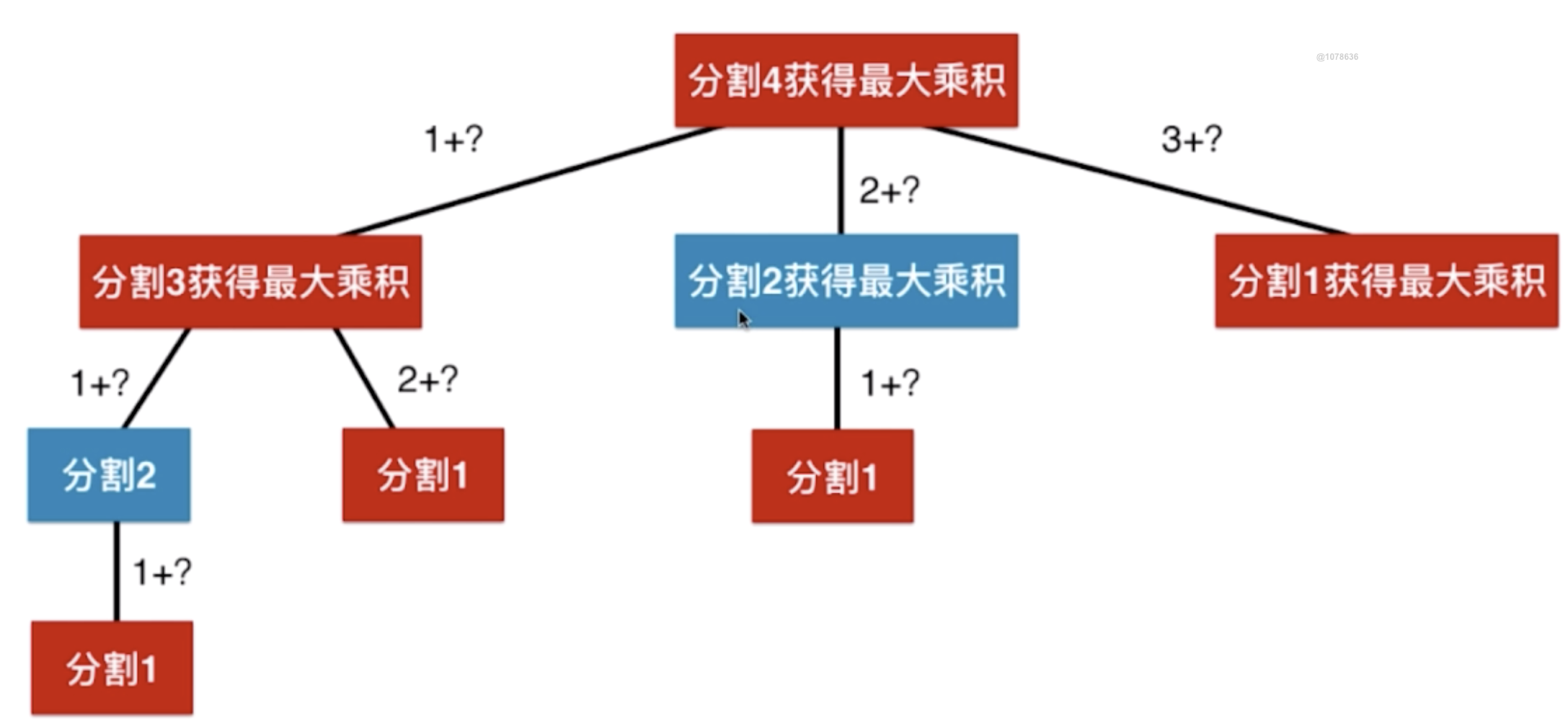

对于分割n而言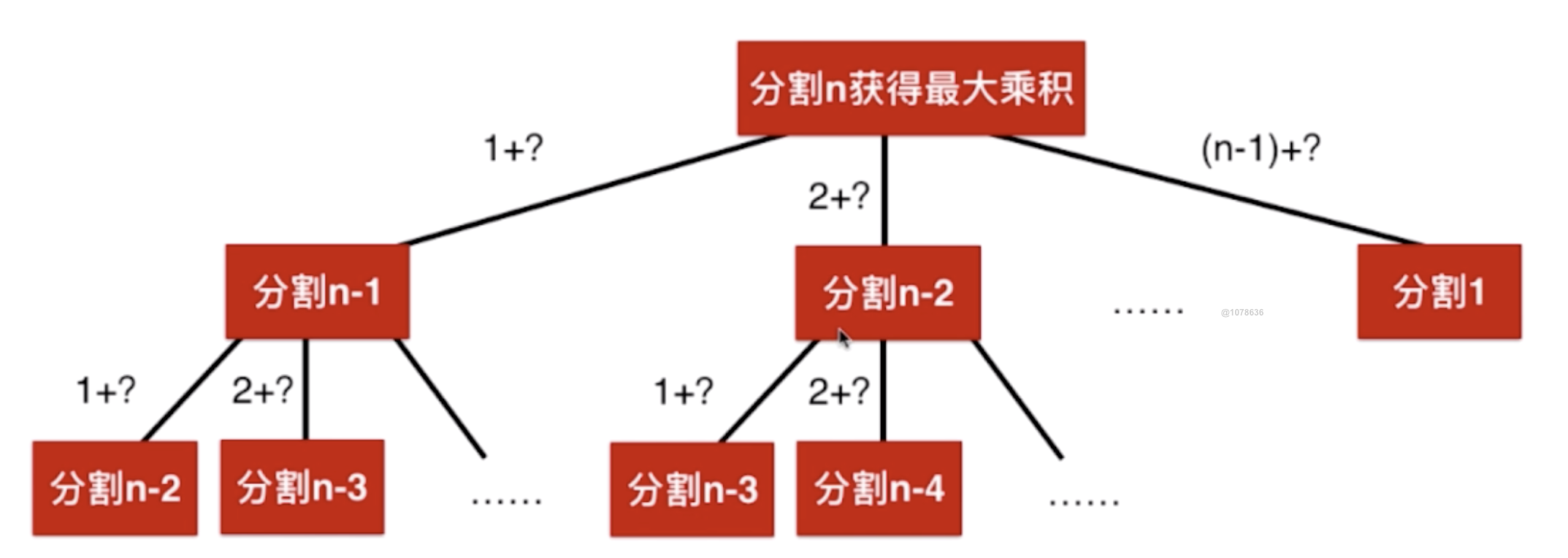

同样存在重叠子问题，可以使用动态规划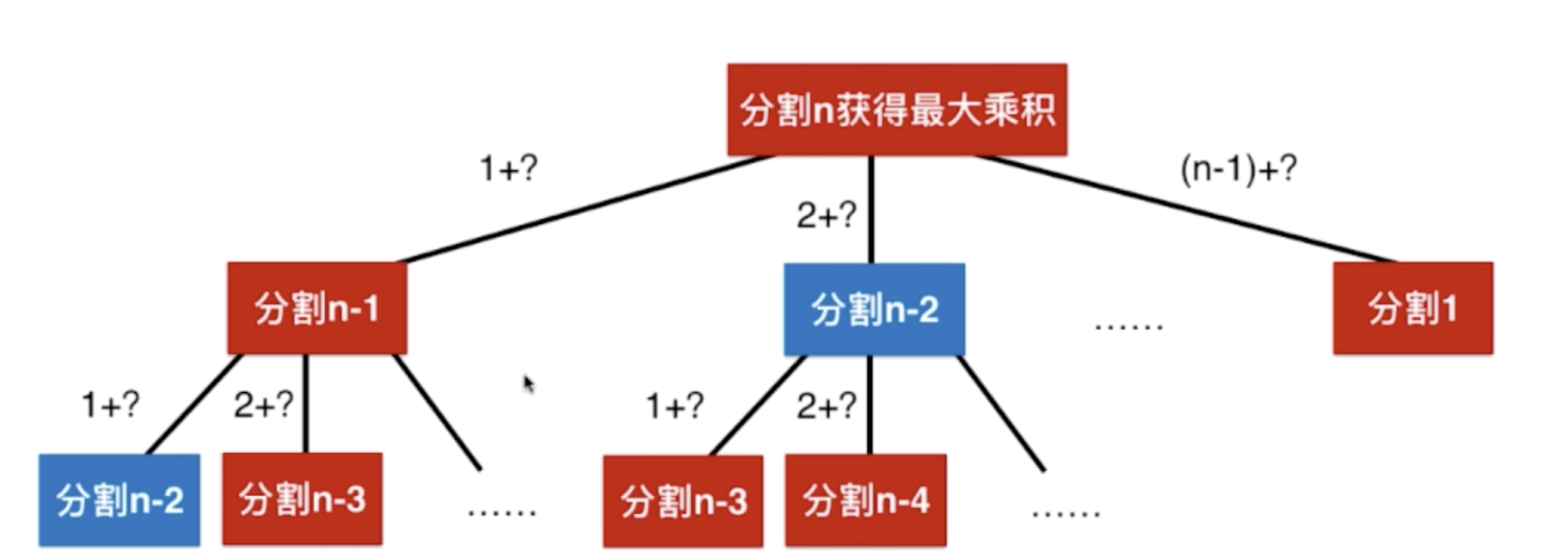

最优子结构

要想知道分割n的最大乘积，如果知道分割n-1，n-2,…1.。那么也就知道了分割n的最大乘积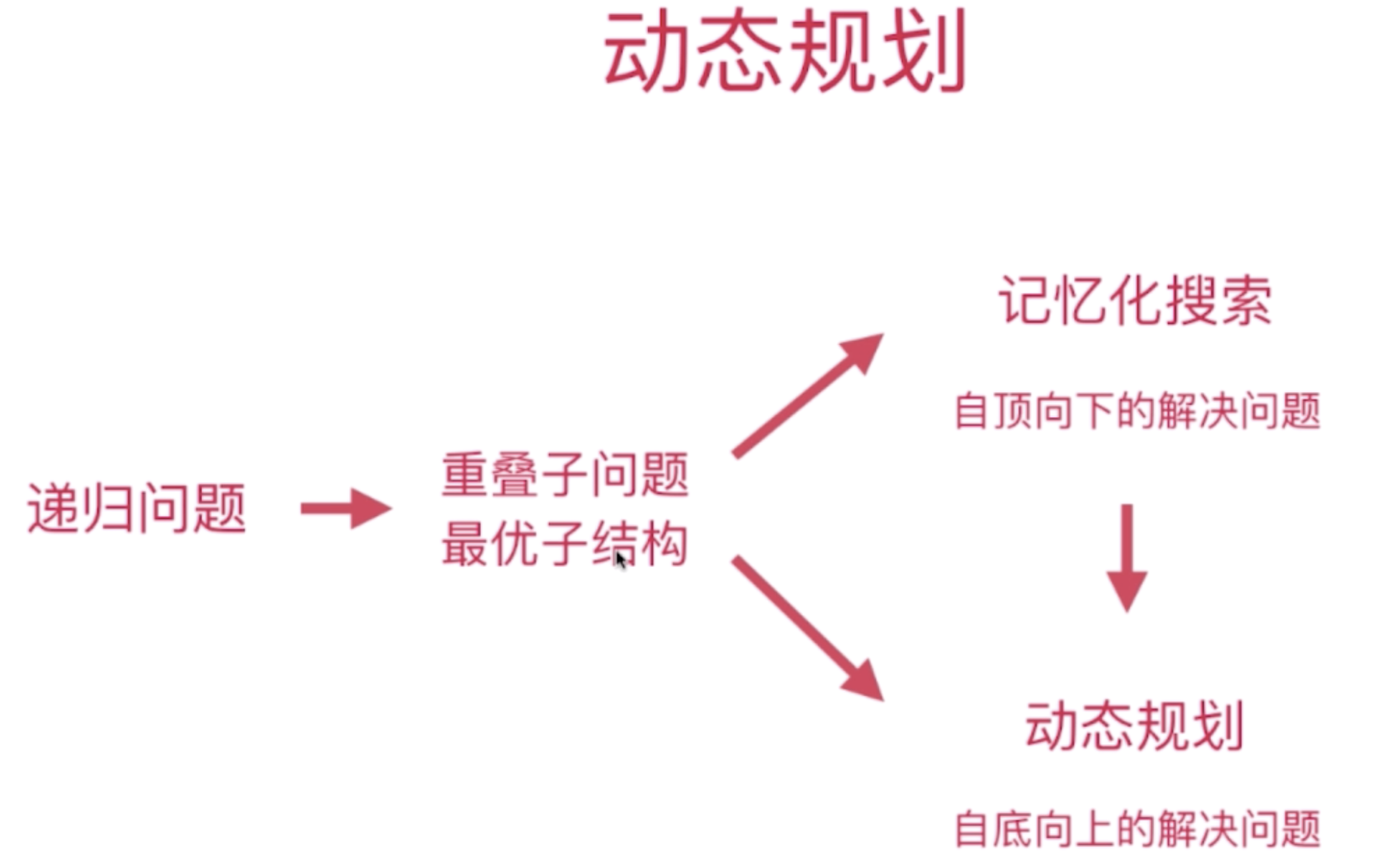

code

递归解法

class Solution {
    //返回三个数的最大值
    private int max3(int a,int b,int c){
        return Math.max(a,Math.max(b,c));
    }
    //将n进行分割(至少分为两部分)，可以获得的最大乘积
    private int breakInteger(int n) {
        //递归终止条件
        if(n==1)
            return 1;
        //遍历所有分割的可能性 每次分割为i + （n-i）这两个数字
        int res = -1;
        for(int i=1;i<=n-1;i++){
            //每次分割为i + （n-i）这两个数字  在这些乘积中寻找最大值
            //这里需要加上n-i不再分割的情况 breakInteger(n-i)表示分割n-i后得到的最大乘积
            res = max3(res,i*(n-i),i * breakInteger(n-i));  //计算n-i的最大分割乘积
        }
        return res;
    }
    public int integerBreak(int n) {
        return breakInteger(n);
    }
}

记忆化搜索 自顶向下

class Solution {
    private int[] memo;   //保存是否计算过
    //返回三个数的最大值
    private int max3(int a,int b,int c){
        return Math.max(a,Math.max(b,c));
    }
    //将n进行分割(至少分为两部分)，可以获得的最大乘积
    private int breakInteger(int n) {
        //递归终止条件
        if(n==1)
            return 1;
        //如果已经计算过，则直接返回
        if(memo[n]!=0)
            return memo[n];
        //遍历所有分割的可能性 每次分割为i + （n-i）这两个数字
        int res = -1;
        for(int i=1;i<=n-1;i++){
            //每次分割为i + （n-i）这两个数字  在这些乘积中寻找最大值
            //这里需要加上n-i不再分割的情况 breakInteger(n-i)表示分割n-i后得到的最大乘积
            res = max3(res,i*(n-i),i * breakInteger(n-i));  //计算n-i的最大分割乘积
        }
        memo[n]=res;   //记录该值已经计算过
        return res;
    }
    public int integerBreak(int n) {
        assert(n>=2);
        memo = new int[n+1];
        return breakInteger(n);
    }
}

动态规划 自底向上

class Solution {
    //返回三个数的最大值
    private int max3(int a,int b,int c){
        return Math.max(a,Math.max(b,c));
    }
    public int integerBreak(int n) {
        //memo[i]表示将数字i分割(至少分割两部分)后得到的最大乘积
        int[] memo = new int[n+1];
        memo[1]=1;
        for(int i=2;i<=n;i++){
            //求解memo[i]
            for(int j=1;j<=i-1;j++){  
                //每一次将其分割为j + (i-j) 对其求最大乘积
                //将i-j分割得到的最大值保存在memo[i-j]中，因为i-j<i所以此时memo[i-j]已经被计算出来了
                //memo[i]保存所有的分割可能的最大值
                memo[i] = max3(memo[i],j*(i-j),j*memo[i-j]);
            }
        }
        return memo[n]; 
    }
}

直接写可能有难度，先研究其递归结构，然后加上记忆化搜索数组，最后自底向上转换为动态规划m