解决思路

滑动窗口+哈希

本问题要求我们返回字符串S 中包含字符串T的全部字符的最小窗口。我们称包含TT的全部字母的窗口为可行窗口。

可以用简单的滑动窗口法来解决本问题。

在滑动窗口类型的问题中都会有两个指针。一个用于延伸现有窗口的 right指针，和一个用于收缩窗口的left 指针。在任意时刻，只有一个指针运动，而另一个保持静止。

本题的解法很符合直觉。我们通过移动right指针不断扩张窗口。当窗口包含全部所需的字符后，如果能收缩，我们就收缩窗口直到得到最小窗口。

答案是最小的可行窗口。

举个例子， S = “ABAACBAB”，T = “ABC”。则问题答案是 “ACB” ，下图是可行窗口中的一个。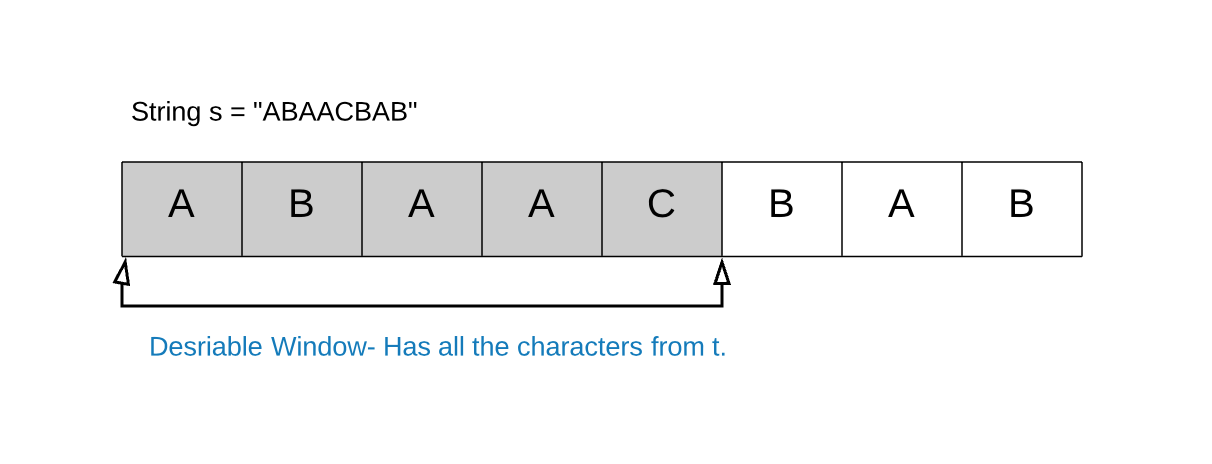

算法

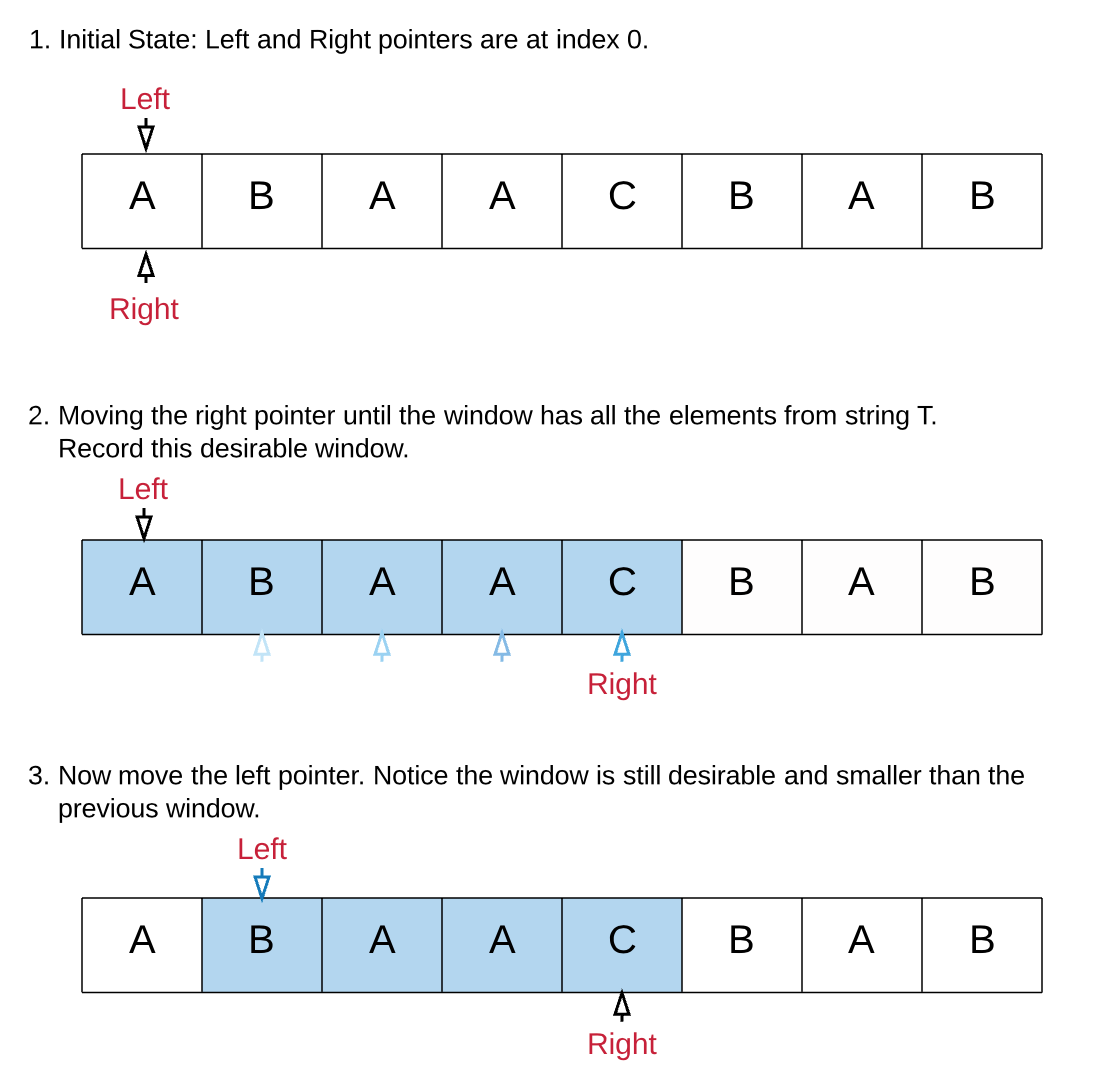
1. 初始，left指针和right指针都指向S的第一个元素.

2. 将 right 指针右移，扩张窗口，直到得到一个可行窗口，亦即包含T的全部字母的窗口。

3. 得到可行的窗口后，将left 指针逐个右移，若得到的窗口依然可行，则更新最小窗口大小。

4. 若窗口不再可行，则跳转至 2。

重复以上步骤，直到遍历完全部窗口。返回最小的窗口。

class Solution {
  public String minWindow(String s, String t) {
      if (s.length() == 0 || t.length() == 0) {
          return "";
      }
      // Dictionary which keeps a count of all the unique characters in t.
      Map<Character, Integer> dictT = new HashMap<Character, Integer>();
      for (int i = 0; i < t.length(); i++) {
          int count = dictT.getOrDefault(t.charAt(i), 0);
          dictT.put(t.charAt(i), count + 1);
      }
      // Number of unique characters in t, which need to be present in the desired window.
      int required = dictT.size();
      // Left and Right pointer
      int l = 0, r = 0;
      // formed is used to keep track of how many unique characters in t
      // are present in the current window in its desired frequency.
      // e.g. if t is "AABC" then the window must have two A's, one B and one C.
      // Thus formed would be = 3 when all these conditions are met.
      int formed = 0;
      // Dictionary which keeps a count of all the unique characters in the current window.
      Map<Character, Integer> windowCounts = new HashMap<Character, Integer>();
      // ans list of the form (window length, left, right)
      int[] ans = {-1, 0, 0};
      while (r < s.length()) {
          // Add one character from the right to the window
          char c = s.charAt(r);
          int count = windowCounts.getOrDefault(c, 0);
          windowCounts.put(c, count + 1);
          // If the frequency of the current character added equals to the
          // desired count in t then increment the formed count by 1.
          if (dictT.containsKey(c) && windowCounts.get(c).intValue() == dictT.get(c).intValue()) {
              formed++;
          }
          // Try and co***act the window till the point where it ceases to be 'desirable'.
          while (l <= r && formed == required) {
              c = s.charAt(l);
              // Save the smallest window until now.
              if (ans[0] == -1 || r - l + 1 < ans[0]) {
                  ans[0] = r - l + 1;
                  ans[1] = l;
                  ans[2] = r;
              }
              // The character at the position pointed by the
              // `Left` pointer is no longer a part of the window.
              windowCounts.put(c, windowCounts.get(c) - 1);
              if (dictT.containsKey(c) && windowCounts.get(c).intValue() < dictT.get(c).intValue()) {
                  formed--;
              }
              // Move the left pointer ahead, this would help to look for a new window.
              l++;
          }
          // Keep expanding the window once we are done co***acting.
          r++;   
      }
      return ans[0] == -1 ? "" : s.substring(ans[1], ans[2] + 1);
  }
}