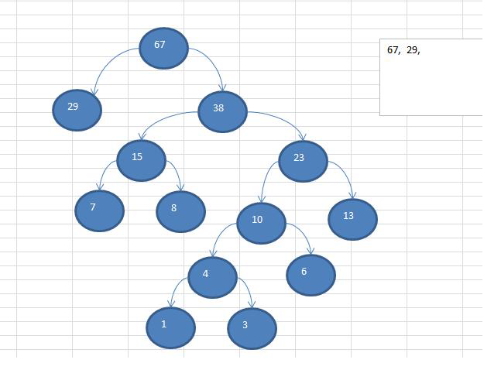
堆排序

基本概念

1)堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。
2)堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆,注意:没有要求结点的左孩子的值和右孩子的值的大小关系。
3)每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆
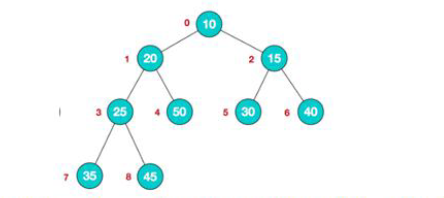
image.png
image.png
一般升序采用大顶堆，降序采用小顶堆

思路

1)将待排序序列构造成一个大顶堆
2)此时，整个序列的最大值就是堆顶的根节点。
3)将其与末尾元素进行交换，此时末尾就为最大值。
4)然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了
可以看到在构建大顶堆的过程中，元素的个数逐渐减少，最后就得到一个有序序列了

图解

建议去网上找,这里就不放了

代码

  1. package com.sgg.algorithm.sort;
  3. import java.util.Arrays;
  5. public class HeapSort {
  7.     public static void main(String[] args) {
  8.         int[] arr = {1,2,3,7,8,9,4,5,6};
  9.         sort(arr);
  10.         System.out.println(Arrays.toString(arr));
  11.     }
  13.     public static void sort(int[] arr) {
  14.         for (int i = arr.length / 2 - 1; i >= 0; i--) {
  15.             adjustHeap(arr, i, arr.length);
  16.         }
  18.         for (int i = arr.length - 1; i > 0; i--) {
  19.             swap(arr, 0, i);
  20.             adjustHeap(arr, 0, i);
  21.         }
  22.     }
  24.     public static void adjustHeap(int[] arr, int i, int length) {
  25.         int temp = arr[i];
  26.         for (int j = 2 * i + 1; j < length; j = j * 2 + 1) {
  27.             if (j + 1 < length && arr[j] < arr[j + 1]) {
  28.                 j++;
  29.             }
  30.             if (arr[j] > temp) {
  31.                 arr[i] = arr[j];
  32.                 i = j;
  33.             } else {
  34.                 break;
  35.             }
  36.         }
  37.         arr[i] = temp;
  38.     }
  40.     public static void swap(int[] arr, int a, int b) {
  41.         int temp = arr[a];
  42.         arr[a] = arr[b];
  43.         arr[b] = temp;
  44.     }
  45. }

赫夫曼树

概念

1)给定n个权值作为n个叶子结点，构造一棵二叉树，若该树的带权路径长度(wpl)达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree),还有的书翻译为霍夫曼树。
2)赫夫曼树是带权路径长度最短的树，权值较大的结点离根较近

定义

1)路径和路径长度：在一棵树中，从一个结点往下可以达到的孩子或孙子结点之间的通路，称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1，则从根结点到第L层结点的路径长度为L-1
2)结点的权及带权路径长度：若将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。结点的带权路径长度为：从根结点到该结点之间的路径长度与该结点的权的乘积
3)树的带权路径长度：树的带权路径长度规定为所有叶子结点的带权路径长度之和，记为WPL(weighted path length) ,权值越大的结点离根结点越近的二叉树才是最优二叉树。
4) WPL最小的就是赫夫曼树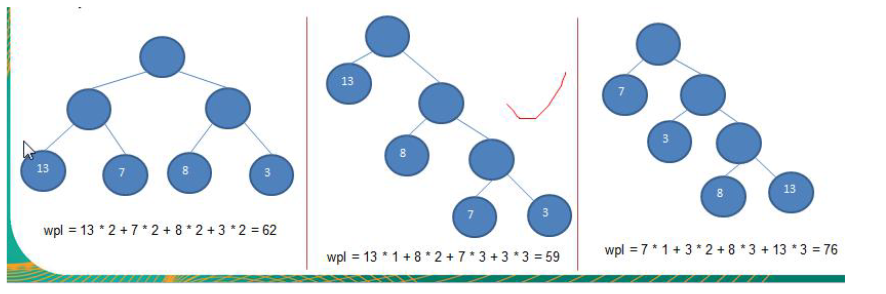
image.png

思路

  • 从小到大进行排序,将每一个数据，每个数据都是一个节点 ， 每个节点可以看成是一颗最简单的二叉树
  • 取出根节点权值最小的两颗二叉树
  • 组成一颗新的二叉树,该新的二叉树的根节点的权值是前面两颗二叉树根节点权值的和
  • 再将这颗新的二叉树，以根节点的权值大小 再次排序， 不断重复1-2-3-4的步骤，直到数列中，所有的数据都被处理，就得到一颗赫夫曼树

image.png

代码

  1. package com.sgg.datastructure.huffmantree;
  3. import java.util.ArrayList;
  4. import java.util.Collections;
  5. import java.util.List;
  7. public class HuffmanTree {
  8.     public static void main(String[] args) {
  9.         int[] arr = {13, 7, 8, 3, 29, 6, 1};
  10.         Node huffmanTree = createHuffmanTree(arr);
  11.         huffmanTree.preOrderPrint();
  12.     }
  14.     /**
  15.      * ● 从小到大进行排序,将每一个数据，每个数据都是一个节点 ， 每个节点可以看成是一颗最简单的二叉树
  16.      * ● 取出根节点权值最小的两颗二叉树
  17.      * ● 组成一颗新的二叉树,该新的二叉树的根节点的权值是前面两颗二叉树根节点权值的和
  18.      * ● 再将这颗新的二叉树，以根节点的权值大小 再次排序， 不断重复1-2-3-4的步骤，直到数列中，所有的数据都被处理，就得到一颗赫夫曼树
  19.      */
  20.     public static Node createHuffmanTree(int[] arr) {
  21.         List<Node> list = new ArrayList<>();
  22.         for (int i : arr) {
  23.             list.add(new Node(i));
  24.         }
  25.         while (list.size() > 1) {
  26.             doFun(list);
  27.         }
  28.         return list.get(0);
  29.     }
  31.     public static void doFun(List<Node> list) {
  32.         Collections.sort(list);
  33.         Node node0 = list.get(0);
  34.         Node node1 = list.get(1);
  35.         Node newNode = new Node(node0.value + node1.value);
  36.         newNode.left = node0;
  37.         newNode.right = node1;
  38.         list.remove(node0);
  39.         list.remove(node1);
  40.         list.add(newNode);
  41.     }
  42. }
  1. package com.sgg.datastructure.huffmantree;
  3. public class Node implements Comparable<Node> {
  4.     Integer value;
  5.     Node left;
  6.     Node right;
  8.     public Node(Integer value) {
  9.         this.value = value;
  10.     }
  12.     @Override
  13.     public String toString() {
  14.         return "Node{" +
  15.                 "value=" + value +
  16.                 '}';
  17.     }
  19.     @Override
  20.     public int compareTo(Node o) {
  21.         return this.value - o.value;
  22.     }
  24.     /**
  25.      * 前序遍历
  26.      */
  27.     public void preOrderPrint() {
  28.         System.out.println(this.value);
  29.         if (this.left != null) {
  30.             this.left.preOrderPrint();
  31.         }
  32.         if (this.right != null) {
  33.             this.right.preOrderPrint();
  34.         }
  35.     }
  38. }

赫夫曼编码

概念

  1. 赫夫曼编码也翻译为哈夫曼编码(Huffman Coding)，又称霍夫曼编码，是一种编码方式,属于一种程序算法
  2. 赫夫曼编码是赫哈夫曼树在电讯通信中的经典的应用之一。
  3. 赫夫曼编码广泛地用于数据文件压缩。其压缩率通常在20%～90%之间

  4. 赫夫曼码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法，称之为最佳编码

    原理

    通信领域中信息的处理方式,主要学习霍夫曼

  5. 定长编码

    1. 英文和数字和空格转成ascii码
    2. 空格作为分隔符?
    3. 40->359 40*8+39=359
  6. 变长编码
    1. 按照各个字符出现的次数进行编码,原则是出现的次数越多,编码越小
    2. 字符编码都不能是其他字符编码的前缀,不能重复匹配(解释二义性就失败了)
  7. 赫夫曼编码(无损压缩)
    1. 统计字符出现次数的权值
    2. 步骤
      1. 从小到大进行排序,将每一个数据，每个数据都是一个节点 ， 每个节点可以看成是一颗最简单的二叉树
      2. 取出根节点权值最小的两颗二叉树
      3. 组成一颗新的二叉树,该新的二叉树的根节点的权值是前面两颗二叉树根节点权值的和
      4. 再将这颗新的二叉树，以根节点的权值大小 再次排序， 不断重复1-2-3-4的步骤，直到数列中，所有的数据都被处理，就得到一颗赫夫曼树
    3. 编码
      1. 根据赫夫曼树，给各个字符,规定编码(前缀编码)， 向左的路径为0向右的路径为1
    4. 特性
      1. 无损压缩,压缩了62.9%
      2. 满足前缀编码,不会造成匹配的多义性
    5. 注意
      1. 注意,这个赫夫曼树根据排序方法不同，也可能不太一样，这样对应的赫夫曼编码也不完全一样，但是wpl是一样的，都是最小的,最后生成的赫夫曼编码的长度是一样
        1. 我们让每次生成的新的二叉树总是排在权值相同的二叉树的最后一个
        2. 我们让每次生成的新的二叉树总是排在权值相同的二叉树的最新一个

创建赫夫曼树

基本结构

  1. package com.sgg.datastructure.huffmancode;
  3. public class Node implements Comparable<Node> {
  4.     Byte data;//数据
  5.     int weight;//权值
  6.     Node left;
  7.     Node right;
  9.     public Node(Byte data, int weight) {
  10.         this.data = data;
  11.         this.weight = weight;
  12.     }
  14.     @Override
  15.     public String toString() {
  16.         return "Node{" +
  17.                 "data=" + data +
  18.                 ", weight=" + weight +
  19.                 '}';
  20.     }
  22.     @Override
  23.     public int compareTo(Node o) {
  24.         return this.weight - o.weight;
  25.     }
  27.     /**
  28.      * 前序遍历
  29.      */
  30.     public void preOrderPrint() {
  31.         System.out.println(this);
  32.         if (this.left != null) {
  33.             this.left.preOrderPrint();
  34.         }
  35.         if (this.right != null) {
  36.             this.right.preOrderPrint();
  37.         }
  38.     }
  39. }

数据压缩

解压缩

二叉排序树

平衡二叉树(AVL树）