栈的一个实际需求

请输入一个表达式
计算式:[722-5+1-5+3-3] 点击计算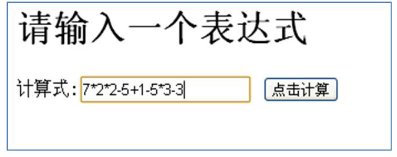
image.png
请问:计算机底层是如何运算得到结果的？
注意不是简单的把算式列出运算,因为我们看这个算式很简单
但是计算机怎么理解这个算式的(对计算机而言，它接收到的就是一个字符串)，我们讨论的是这个问题。

栈的介绍

1)栈的英文为(stack)
2)栈是一个先入后出(FILO-First In Last Out)的有序列表。
3)栈(stack)是限制线性表中元素的插入和删除只能在线性表的同一端进行的一种特殊线性表。允许插入和删除的
一端，为变化的一端，称为栈顶(Top)，另一端为固定的一端，称为栈底(Bottom)。
4)根据栈的定义可知，最先放入栈中元素在栈底，最后放入的元素在栈顶，而删除元素刚好相反，最后放入的元
素最先删除，最先放入的元素最后删除
5)图解方式说明出栈(pop)和入栈(push)的概念尚硅谷Java数据结构和算法

栈的应用场景

  1. 子程序的调用：在跳往子程序前，会先将下个指令的地址存到堆栈中，直到子程序执行完后再将地址取出，以回到原来的程序中。
  2. 处理递归调用：和子程序的调用类似，只是除了储存下一个指令的地址外，也将参数、区域变量等数据存入堆栈中。
  3. 表达式的转换[中缀表达式转后缀表达式]与求值(实际解决)。
  4. 二叉树的遍历。

  5. 图形的深度优先(depth一first)搜索法。

    栈的快速入门

  6. 用数组模拟栈的使用，由于栈是一种有序列表，当然可以使用数组的结构来储存栈的数据内容，
    下面我们就用数组模拟栈的出栈，入栈等操作。

  7. 实现思路分析,并画出示意图

    数组实现

    1. /**
    2. * 数组实现
    3. * 0.存储数据
    4. * 1.构造器
    5. * 2.满
    6. * 3.空
    7. * 4.push
    8. * 5.pop
    9. * 6.遍历
    10. */
    11. public class ArrayStack {
    12.  private int[] array;
    13.  private int size;
    14.  private int top=-1;
    16.  public ArrayStack(int size) {
    17.      this.size = size;
    18.      array = new int[size];
    19.  }
    21.  public int getSize() {
    22.      return size;
    23.  }
    25.  public boolean isFull(){
    26.      return top == size - 1;
    27.  }
    29.  public boolean isEmpty(){
    30.      return top == -1;
    31.  }
    33.  public void push(int val) {
    34.      if (isFull()) {
    35.          throw new RuntimeException("栈已满,无法push");
    36.      }
    37.      top++;
    38.      array[top] = val;
    39.  }
    41.  public int pop(){
    42.      if (isEmpty()) {
    43.          throw new RuntimeException("栈是空的,无法pop");
    44.      }
    45.      int result = array[top];
    46.      top--;
    47.      return result;
    48.  }
    50.  public void show(){
    51.      for (int i = top; i >=0 ; i--) {
    52.          System.out.printf("stack[%d]=%d\n",i,array[i]);
    53.      }
    54.  }
    56.  public static void main(String[] args) {
    57.      ArrayStack arrayStack = new ArrayStack(5);
    58.      arrayStack.push(1);
    59.      arrayStack.push(2);
    60.      arrayStack.push(3);
    61.      arrayStack.push(4);
    62.      arrayStack.push(5);
    63.      arrayStack.show();
    64.      System.out.println(arrayStack.pop());
    65.      System.out.println(arrayStack.pop());
    66.      System.out.println(arrayStack.pop());
    67.  }
    68. }

    第一次用双链表

    ```java package com.sgg.datastructure.stack;

/**

  • 链表实现
  • 0.存储数据
  • 1.构造器
  • 2.满
  • 3.空
  • 4.push
  • 5.pop

  • 6.遍历 */ public class LinkStackTwo { private StackNodeTwo top;

    public boolean isFull() {

    1.  return false;

    }

    public boolean isEmpty() {

    1.  return top == null;

    }

    public void push(int i) {

    1.  if (top == null) {
    2.      top = new StackNodeTwo(i);
    3.      top.next = top;
    4.      top.prev = top;
    5.  } else {
    6.      StackNodeTwo node = new StackNodeTwo(i);
    7.      top.next = node;
    8.      node.prev = top;
    9.      top = node;
    10.  }

    }

    public int pop() {

    1.  if (isEmpty()) {
    2.      throw new RuntimeException("空了");
    3.  }
    4.  int no = top.no;
    5.  if (top != top.prev) {
    6.      top = top.prev;
    7.  } else {
    8.      top = null;
    9.  }
    10.  return no;

    }

    public void show() {

    1.  StackNodeTwo temp = top;
    2.  while (true) {
    3.      System.out.printf("遍历%d\n",temp.no);
    4.      temp = temp.prev;
    5.      if (temp.prev == temp) {
    6.          System.out.println("遍历"+temp.no);
    7.          break;
    8.      }
    9.  }

    }

    public static void main(String[] args) {

    1.  LinkStackTwo linkStack = new LinkStackTwo();
    2.  linkStack.push(1);
    3.  linkStack.push(2);
    4.  linkStack.push(3);
    5.  linkStack.push(4);
    6.  linkStack.show();
    7.  System.out.println(linkStack.pop());
    8.  System.out.println(linkStack.pop());
    9.  System.out.println(linkStack.pop());
    10.  System.out.println(linkStack.pop());

    } }

  1. <a name="Adk4u"></a>
  2. ## 第二次看别人用单链表更合理
  3. ```java
  4. package com.sgg.datastructure.stack;
  6. /**
  7.  * 链表实现
  8.  * 0.存储数据
  9.  * 1.构造器
  10.  * 2.满
  11.  * 3.空
  12.  * 4.push
  13.  * 5.pop
  14.  * 6.遍历
  15.  */
  16. public class LinkStackOne {
  17.     private StackNodeOne top;
  19.     public boolean isEmpty() {
  20.         return top == null;
  21.     }
  23.     public void push(int i) {
  24.         StackNodeOne node = new StackNodeOne(i);
  25.         node.next = top;
  26.         top = node;
  27.     }
  29.     public int pop() {
  30.         if (isEmpty()) {
  31.             throw new RuntimeException("空");
  32.         }
  33.         int no = top.no;
  34.         top = top.next;
  35.         return no;
  36.     }
  38.     public void show() {
  39.         StackNodeOne temp = top;
  40.         while (temp != null) {
  41.             System.out.println("loop" + temp.no);
  42.             temp = temp.next;
  43.         }
  44.     }
  46.     public static void main(String[] args) {
  47.         LinkStackOne linkStack = new LinkStackOne();
  48.         linkStack.push(1);
  49.         linkStack.push(2);
  50.         linkStack.push(3);
  51.         linkStack.push(4);
  52.         linkStack.show();
  53.         System.out.println(linkStack.pop());
  54.         System.out.println(linkStack.pop());
  55.         System.out.println(linkStack.pop());
  56.         linkStack.push(5);
  57.         linkStack.push(6);
  58.         linkStack.push(7);
  59.         linkStack.show();
  60.     }
  61. }

利用栈,实现计算器

中缀直接计算

思路

1.遍历字符串,把数字和操作符分别放到2个栈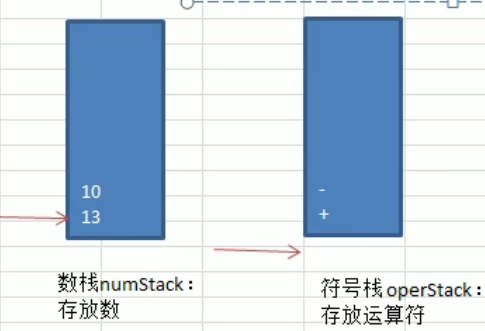
image.png
2.数字就是无脑入栈
3.操作符入栈有以下几种情况

  • 操作符栈顶为空
  • 当前操作符的优先级小于或者等于操作符栈顶的,取出栈顶,pop2个数,计算,入数栈,当前操作符入栈
  • 优先级大于,入栈

4.pop运算
5.只剩下一个就行

代码实现

代码有bug 先不管到时候用其他的实现
src=http---img3.doubanio.com-view-group_topic-l-public-p293455180.jpg&refer=http---img3.doubanio.jpg

后缀表达式

思路

3 4 + 5 × 6 -的计算
1.从左至右扫描，将3和4压入堆栈；
2.遇到+运算符，因此弹出4和3（4为栈顶元素，3为次顶元素，注意与前缀表达式做比较），计算出3+4的值，得7，再将7入栈；
3.将5入栈；
4.接下来是×运算符，因此弹出5和7，计算出7×5=35，将35入栈；
5.将6入栈；
6.最后是-运算符，计算出35-6的值，即29，由此得出最终结果。

代码

  1. public class 后缀表达式计算器 {
  3.     public static String cal(String expression) {
  4.         Stack<String> stack = new Stack<>();
  5.         List<String> list = StrUtil.split(expression, StrUtil.SPACE);
  6.         for (String str : list) {
  7.             if (NumberUtil.isNumber(str)) {
  8.                 stack.push(str);
  9.             }else {
  10.                 Integer pop1 = Integer.valueOf(stack.pop());
  11.                 Integer pop2 = Integer.valueOf(stack.pop());
  12.                 Integer result = calOne(pop1, pop2, str);
  13.                 stack.push(result+"");
  14.             }
  15.         }
  16.         String result = stack.pop();
  17.         System.out.printf("后缀表达式:%s = %s\n",expression,result);
  18.         return result;
  19.     }
  21.     private static Integer calOne(Integer pop1, Integer pop2, String str) {
  22.         Integer result = null;
  23.         switch (str) {
  24.             case "+":
  25.                 result = pop2 + pop1;
  26.                 break;
  27.             case "-":
  28.                 result = pop2 - pop1;
  29.                 break;
  30.             case "*":
  31.                 result = pop2 * pop1;
  32.                 break;
  33.             case "/":
  34.                 result = pop2 / pop1;
  35.                 break;
  36.             default:
  37.                 throw new RuntimeException("参数有误");
  38.         }
  39.         return result;
  40.     }
  42.     public static void main(String[] args) {
  43.         String expression = "3 4 + 5 * 6 -";//29
  44.         cal(expression);
  45.         String expression2 = "4 5 * 8 - 60 + 8 2 / +";//76
  46.         cal(expression2);
  47.     }
  48. }

结果

后缀表达式:3 4 + 5 6 - = 29
后缀表达式:4 5 8 - 60 + 8 2 / + = 76
用后缀表达式计算结果还是很简单的

中缀表达式->后缀表达式

思路

  1. 初始化两个栈：运算符栈s1和储存中间结果的栈s2；
  2. 从左至右扫描中缀表达式；
  3. 遇到操作数时，将其压s2；
  4. 遇到运算符时，比较其与s1栈顶运算符的优先级：
    1. 如果s1为空，或栈顶运算符为左括号“(”，则直接将此运算符入栈；
    2. 否则，若优先级比栈顶运算符的高，也将运算符压入s1；
    3. 否则，将s1栈顶的运算符弹出并压入到s2中，再次转到(4-1)与s1中新的栈顶运算符相比较；
  5. 遇到括号时：
    (1)如果是左括号“(”，则直接压入s1
    (2)如果是右括号“)”，则依次弹出s1栈顶的运算符，并压入s2，直到遇到左括号为止，此时将这一对括号丢弃
  6. 重复步骤2至5，直到表达式的最右边
  7. 将s1中剩余的运算符依次弹出并压入s2
  8. 依次弹出s2中的元素并输出，结果的逆序即为中缀表达式对应的后缀表达式

    代码

    ```java package com.sgg.datastructure.stack;

import cn.hutool.core.util.StrUtil;

import java.util.ArrayList; import java.util.Arrays; import java.util.List; import java.util.Stack;

public class 表达式 { public static List 中缀转后缀(String expression) { Stack operate = new Stack<>(); List result = new ArrayList<>();//可以用arraylist替代 List split = toInfixExpressionList(expression);//没有考虑超过2位数的数字拼接 for (String str : split) { if (StrUtil.isNumeric(str)) { result.add(str); } else if (isOperate(str)) { while (true) { if (operate.isEmpty() || StrUtil.equals(operate.peek(), “(“)) { operate.push(str); break; } else if (isPriority(str, operate.peek())) { operate.push(str); break; } else { String pop = operate.pop(); result.add(pop); } } } else if (StrUtil.equals(“(“, str)) { operate.push(str); } else if (StrUtil.equals(“)”, str)) { String ele; while (true) { ele = operate.pop(); if (StrUtil.equals(ele, “(“)) { break; } else { result.add(ele); } } } else { throw new RuntimeException(“参数有误”); } } while (!operate.isEmpty()) { String pop = operate.pop(); result.add(pop); } return result; }

  1. private static boolean isPriority(String str, String peek) {
  2.     return getScore(str) > getScore(peek);
  3. }
  5. private static int getScore(String str) {
  6.     switch (str) {
  7.         case "+":
  8.         case "-":
  9.             return 1;
  10.         case "*":
  11.         case "/":
  12.             return 2;
  13.         default:
  14.             throw new RuntimeException("参数有误");
  15.     }
  16. }
  19. public static boolean isOperate(String str) {
  20.     List<String> list = Arrays.asList("+", "-", "*", "/");
  21.     return list.contains(str);
  22. }
  24. public static List<String> toInfixExpressionList(String expression) {
  25.     List<String> result = new ArrayList<>();
  26.     String ele = "";
  27.     String[] split = StrUtil.split(expression, 1);
  28.     for (String raw : split) {
  29.         if (StrUtil.isNumeric(raw)) {
  30.             ele += raw;
  31.         } else {
  32.             if (StrUtil.isNotBlank(ele)) {
  33.                 result.add(ele);
  34.                 ele = "";
  35.             }
  36.             result.add(raw);
  37.         }
  38.     }
  39.     if (StrUtil.isNotBlank(ele)) {
  40.         result.add(ele);
  41.     }
  42.     return result;
  43. }
  46. public static void main(String[] args) {
  47.     String middle = "1+((2+3)*41)-20";
  48.     List<String> ex = 中缀转后缀(middle);
  49.     System.out.println(ex);
  50.     System.out.println(后缀表达式计算器.cal(StrUtil.join(StrUtil.SPACE, ex)));
  51. }

}

```

总结

思路挺难的,是数学和计算机思维,主要学应用和思想!