1. 面试题
  2. 技巧
  3. 位运算（以前用过）与异或运算（魔性）

定义与性质

  1. 异或运算：相同为0，不同为1
  2. 同或运算：相同以1，不同为0.

(能长时间记住的概率接近0%)

  1. 异或运算就记成**无进位相加**！（相加不进位）
  2. 性质：
    1. 0^N=N
    2. N^N=0
    3. A^B=B^A===>交换律
    4. (A^B)^C=A^(B^C)===>结合律
    5. 结合c和d，同样一批数，不管选择什么样的顺序，最终结果应该是一样的
  3. 无进位相加在多个数的情况下也适用，并且多个数无进位相加改变顺序不改变结果（偶数个1是0，奇数个1是1）

image.png

  1. 最根本的性质为无进位相加这一个性质
  2. 用途、作用、题目：
    1. 如何不用额外变量交换两个数？
    2. 一个数组中有-一种数出现了奇数次，其他数都出现了偶数次，怎么找到并打印这种数
    3. 怎么把一个int类型的数，提取出最右侧的1来
    4. 一个数组中有两种数出现了奇数次，其他数都出现了偶数次，怎么找到并打印这两种数
    5. 一个数组中有一种数出现K次，其他数都出现了M次，（M>1,K<M）找到出现了K次的数,。要求：额外空间复杂度O(1)，时间复杂度O(N)。

如何不用额外变量交换两个数（额外变量+求和交换+异或交换）

  1. 综合运用异或的性质
  2. 主要使用N^N=0和0^N=N
  3. 异或运算的效率高于加减法的效率
  4. 位运算效率最高！！！
  5. 证明：

image.png

  1. ❗注意点：只有在a和b指的是**两块不同的内存区域**时，这种交换的方法才会生效；假如在一个内存位置进行交换，会将这个内存位置刷为0；一直是同一个变量在与自己做异或运算并赋值给自己（即第一步将自己变为0，后两部都为0^0=0）

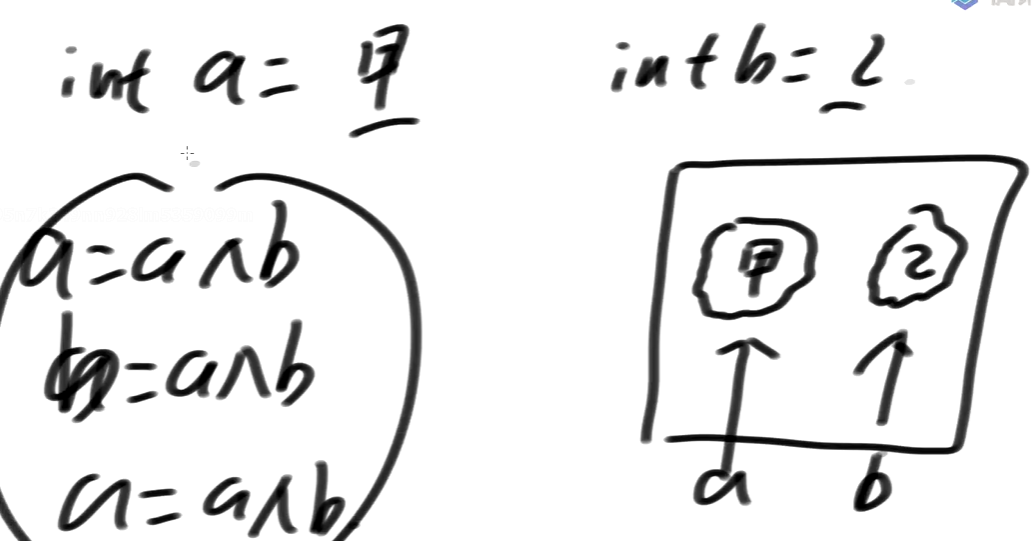
image.png image.png

  1. 有时候不要装逼，要注意使用条件，老老实实写交换；要上游可以保证不是对同一内存进行交换才可以这么用，不能保证最好不要这么用；拿捏不住尺寸，最好还是老老实实写原来的交换
  2. 在java中这么写其实没什么好处，但面试官可能会问这种恶心的，自己当了面试官不要这么问🤔
  3. 底层程序员、写操作系统的程序员、用汇编语言的程序员会经常用到这种操作！！！
  4. 底层一般全是位运算，上层程序员很少用（同事看不懂就离谱）（编译器优化？），注重性能的地方一般这么用
  5. 脚本语言或者一些优化过的语言有可能位运算和加减运算一样快也是有可能的！
  1. a = a ^ b;        //int tmp = a;
  2. b = a ^ b;        //a = b;
  3. a = a ^ b;        //b = tmp;

一个数组中有一种数出现了奇数次，其他数都出现了偶数次，怎么找到并打印这种数

  1. 哈希表词频统计，每种词记录出现的频数===>装逼失败，优化空间复杂度===>用一个变量找到
  2. 异或运算处理：初始化一变量eor=0，一次把所有值都与eor异或起来，最终的eor就是我们要求的结果（即奇数次的数字）
  3. 使用了异或运算的交换律和结合律：
    1. 偶数个同一数据异或起来结果为0
    2. 奇数个同一数据异或起来结果为该数据本身
  4. 不是装逼，这种方法确实好，只要一个变量即可（额外空间复杂度降为O(1)===>常数空间）

怎么把一个int类型的数，提取出最右侧的1来（常规操作）

  1. 这是一个常规操作，虽然现在看起来蛋疼，但是这种方式是大量使用到的
  2. 题意：将该数写成二进制的形式，只保留住最后一位1，其余为都变为0，这就是想要的数
  3. 解答：结果=a&(-a)=a&(~a+1)
  4. 原理1（补码角度）：从补码的角度考虑，对a取反加1就是求a的相反数的补码（取反包括了符号位，不包括符号位就是a的补码===>正数的补码是本身，负数的补码……）；又因为计算机中整数以补码的形式存在，并且取反包括了符号位，所以能够在相与的过程中将前面的位都置为0，而最后一位1因为加了1所以仍旧保持1===>负数补码的便捷求法：符号位保持为1，保持最后一位1不变，将除最后一位1所在位之前的所有位都取反
  5. 原理2（直观角度）：取反的时候将最后一位1的左边的每一位都取反了，最后一位1会被搞成0，最后一位1右侧所有的0都会变为1===>相当于最后一位1左侧都取相反状态，并且把最后一位1打散了（拆散：最后一位1会被搞成0，最后一位1右侧所有的0都会变为1，用0进行分隔）；对打散的状态再加个1还原回来（拧回来，合回来）；最后一“与”就得到了结果（最后一位1）
  6. 在机器中整数是按补码形式存储的，正数的补码是他本身，负数的补码是将除符号位外的部分取反再整体加1

image.png

一个数组中有两种数出现了奇数次，其他数都出现了偶数次，怎么找到并打印这两种数

  1. 两种数出现了奇数次，因为是两种数，所以这两种数一定不一样
  2. 将所有的数与到eor上去，结果为eor=a^b;
  3. 因为a和b不相等，所以eor≠0;===>找eor中找为1的位置（哪个都行）===>刚才求得了最右的1（提取出一个数最右侧的1）
  4. 为1的位置说明a的该位置和b的该位置不一样
  5. 将整个数组分为如下两类（对于arr中所有的数）：
    1. 上述4中位置上为1的数；
    2. 上述4中位置上为0的数；
    3. 设a的位置为1，b的位置为0；还是a的位置为0，b的位置为1；这两种都是一样的，反正这两种必然分开
    4. 这两类中包括那些出现了偶数次的数
  6. 再设一变量eor’，eor’=上述5中两类中某一类中的元素异或起来的值===>这样就得到了两个出现奇数次的数的其中一个（把其中一个给拽出来了）
  7. 最后再将eor^eor’，结果就为另一出现奇数次的数
  8. 这样两个数都被得到了
  9. 通过异或之后的某一位为1的位将数组分类，其中两个出现奇数次的数分别位于这两类中，并且其余的数也被分配到这两类中去了且都为偶数个，不会对结果产生影响===>最根本的目的就是为了将出现奇数次的两个数分离开来（分离为1不为1的目的就在于此，不是为了避免同一位上不同造成的影响—->这没有影响）
  10. 正负数都一样===>因为用补码表示，可以统一计算！
  11. eor’中的’在java中不合法
  12. 假设a为小的那个，b为大的那个该怎么比===>直接用大于号和小于号？
  13. 举例：a=6，b=10

一个数组中两种数出现了奇数次-min.gif

  1. package class01;
  3. public class Code07_EvenTimesOddTimes {
  5.     // arr中，只有一种数，出现奇数次
  6.     public static void printOddTimesNum1(int[] arr) {
  7.         int eor = 0;
  8.         for (int i = 0; i < arr.length; i++) {
  9.             eor ^= arr[i];
  10.         }
  11.         System.out.println(eor);
  12.     }
  14.     // arr中，有两种数，出现奇数次
  15.     public static void printOddTimesNum2(int[] arr) {
  16.         int eor = 0;
  17.         for (int i = 0; i < arr.length; i++) {
  18.             eor ^= arr[i];
  19.         }
  20.         // eor = a ^ b ===> a和b是两种数
  21.         // eor != 0
  22.         // eor必然有一个位置上是1
  23.         // 0110010000
  24.         // 0000010000
  25.         int rightOne = eor & (~eor + 1); // 提取出最右的1
  26.         int onlyOne = 0; // eor'
  27.         for (int i = 0 ; i < arr.length;i++) {
  28.             //  arr[1] =  111100011110000
  29.             // rightOne=  000000000010000
  30.             if ((arr[i] & rightOne) != 0) {
  31.                 onlyOne ^= arr[i];
  32.             }
  33.         }
  34.         System.out.println(onlyOne + " " + (eor ^ onlyOne));
  35.     }
  37.     // 该方法用于统计N的二进制中1出现的次数（个数）
  38.     public static int bit1counts(int N) {
  39.         int count = 0;
  41.         //   011011010000
  42.         //   000000010000     1
  44.         //   011011000000
  45.         // 
  49.         while(N != 0) {
  50.             int rightOne = N & ((~N) + 1);
  51.             count++;
  52.             N ^= rightOne;
  53.             // N -= rightOne
  54.         }
  57.         return count;
  59.     }
  62.     public static void main(String[] args) {
  63.         int a = 5;
  64.         int b = 7;
  66.         a = a ^ b;
  67.         b = a ^ b;
  68.         a = a ^ b;
  70.         System.out.println(a);
  71.         System.out.println(b);
  73.         int[] arr1 = { 3, 3, 2, 3, 1, 1, 1, 3, 1, 1, 1 };
  74.         printOddTimesNum1(arr1);
  76.         int[] arr2 = { 4, 3, 4, 2, 2, 2, 4, 1, 1, 1, 3, 3, 1, 1, 1, 4, 2, 2 };
  77.         printOddTimesNum2(arr2);
  79.     }
  81. }

一个数组中有一种数出现K次，其他数都出现了M次，（M>1,K<M）找到出现了K次的数。要求：额外空间复杂度O(1)，时间复杂度O(N)。

  1. 额外空间复杂度O(1)的意思是说用有限几个变量就能做出来，而不是只能用一个变量
  2. 任何一个数都能转换为数组形式的二进制状态===>用长度为32的数组额外空间复杂度依旧为O(1)
  3. 负数没影响=>因为我们是用状态信息来搞的
  4. 思路：
    1. 定义一个长度为32的数组（存放所有数中各位置为1出现的次数）===>int类型，假如词频统计过多也可以使用long类型
    2. 将每一个数（int类型）都转换为数组形式的二进制状态并将其加到a中定义的数组中去
    3. 对所定义的数组进行遍历
      1. 假如某一位可以整除M，则出现K次的那个数该位置上为0
      2. 假如某一位不可以整除M，则出现K次的那个数该位置上为1
      3. 因为有M>1与K<M的限制，所以不存在K是M的倍数的关系；并且一个数出现了K次，多个数出现了M次，所以一共有多个数的个数*M+K个数
  5. 代码中虽然有一个双层循环，但是内层循环是固定为32次的，只有外层循环需要根据数组大小而产生变化，所以最高阶依然是n，去掉常数后依旧为O(n)
  6. 先开始通过&分离每一位，最后通过|设置进去(相加也行，因为每一位只操作一次并且都是加1，不会出现进位)
  7. 用对数器能够最快提高自己的能力===>用对数器做测试，有oj用oj
  1. package class01 ;
  2. public class Code08_ _KM {
  4.     // 使用对数器验证代码是否正确
  5.     // 对数器的代码想写多烂就写多烂，只要能保证对就行，不对也可以调
  6.     // 先写经典解，用hash表法进行解题：统计词频
  7.     public static int test(int口 arr, int k, int m) {
  8.         HashMap<Integer, Integer> map = new HashMap<>O);
  9.         for (int num : arr) {
  10.             if (map.containsKey(num)) {
  11.                 map.put( num, map. get(num) + 1);
  12.             } else {
  13.                 map.put(num, 1);
  14.             }
  15.         }
  16.         for (int num : map.keySet()) {    // 获取键的集合
  17.             if (map.get(num) == k) {    // 看键所对应的值是否为K
  18.                 return num;
  19.             }
  20.         }
  21.         return -1;
  22.     }
  26.     //请保证arr中，只有一种数出现了K次，其他数都出现了M次
  27.     public static int onlyKTimes(int[] arr, int k, int m) {
  28.         int[] t = new int[32];
  29.         // t[0] 0位置的1出现了几个
  30.         // t[i] i位置的1出现了几个
  31.         for (int num : arr) {
  32.             for(inti=0;i<=31;i++){
  33.                 t[i]+=(num>>i)&1;
  34.             }
  35.         }
  36.         int ans = 0;
  37.         for(int i=0; i<32; i++){
  38.             if (t[i] % m != 0){    //在第i位上，有1
  39.                 ans|=(1 << i);     
  40.             }
  41.         return ans;
  42.     }
  44.     // 随机生成数组
  45.     public static int[] randomArray(int maxKinds， int range, int k, int m) {
  46.         int ktimeNum = randomNumber(range);
  47.         // 2===>至少两种数
  48.         int numKinds = (int)(Math.random() * maxKinds) + 2;
  49.         //k * 1 + (numKinds - 1) * m===>总个数（数组长度）
  50.         int[] arr = new int[k + (numKinds - 1) * m];
  51.         int index = 0;
  52.         for( ;index < k;index++) {
  53.             arr[index] = ktimeNum;
  54.             numKinds--;
  55.         }
  56.         numKinds--;
  57.         HashSet<Integer> set = new HashSet<>() ;
  58.         set.add(ktimeNum);|
  59.         while(numKinds != 0) {
  60.             int curNum = 0;
  61.             do {
  62.                 curNum = randomNumber(range);
  63.             }while(set.contains(curNum));
  64.             set.add(curNum);
  65.             numKinds-- ;
  66.             for(inti=0; i<m; i++){
  67.                 arr[index++] = curNum;
  68.             }
  69.         }// arr填好了
  71.         // 打乱数组（太有顺序了）
  72.         for (int i = 0; i < arr.length; i++) {
  73.             // i位置的数,我想随机和j位置的数做交换
  74.             int j = (int)(Math.random() * arr.length);// 0 ~ N-1
  75.             int tmp = arr[i];
  76.             arr[i] = arr[j];
  77.             arr[j] = tmp;
  78.         }
  79.         return arr; 
  80.     }
  83.     // 题目升级===>出现了k次就返回出现了k次的数，没有出现k次就返回-1
  84.     public static int onlyKTimesPlus(int[] arr, int k, int m) {
  85.         int[] t = new int[32];
  86.         // t[0] 0位置的1出现了几个
  87.         // t[i] i位置的1出现了几个
  88.         for (int num : arr) {
  89.             for(inti=0;i<=31;i++){
  90.                 t[i]+=(num>>i) & 1;
  91.             }
  92.         }
  93.         int ans = 0;
  94.         for(int i=0; i<32; i++){ 
  95.             // 题目升级===>出现了k次就返回出现了k次的数，没有出现k次就返回-1
  96.             if(t[i] % m == 0) {
  97.                 continue;
  98.             }
  99.             if(t[i] % m == k) {
  100.                 ans |= (1 << i);
  101.             }else {
  102.                 return -1;
  103.             }
  104.             /**
  105.             错误写法
  106.             if (t[i] % m != 0 && t[i] % m == k) {
  107.                 ans |= (1 << i);
  108.             } else {
  109.                 return -1;
  110.             }
  111.             */
  112.         }
  113.         return ans;
  114.     }
  116.     // 随机生成数组
  117.     public static int[] randomArrayPlus(int maxKinds， int range, int k, int m) {
  118.         int ktimeNum = randomNumber(range);
  120.         //真命天子出现的次数
  121.         // 以0.5（50%）的概率决定是k次，还是一个随机次的但是一定比m小的次数
  122.         int times = Math.random() < 0.5 ? k : ((int)(Math.random() * (m - 1)) + 1);
  124.         // 2===>至少两种数
  125.         int numKinds = (int)(Math.random() * maxKinds) + 2;
  126.         //k * 1 + (numKinds - 1) * m===>总个数（数组长度）
  127.         // 参数k没用了
  128.         int[] arr = new int[times + (numKinds - 1) * m];
  129.         int index = 0;
  130.         for( ;index < k;index++) {
  131.             arr[index] = ktimeNum;
  132.             numKinds--;
  133.         }
  134.         numKinds--;
  135.         HashSet<Integer> set = new HashSet<>() ;
  136.         set.add(ktimeNum);|
  137.         while(numKinds != 0) {
  138.             int curNum = 0;
  139.             do {
  140.                 curNum = randomNumber(range);
  141.             }while(set.contains(curNum));
  142.             set.add(curNum);
  143.             numKinds-- ;
  144.             for(inti=0; i<m; i++){
  145.                 arr[index++] = curNum;
  146.             }
  147.         }// arr填好了
  149.         // 打乱数组（太有顺序了）
  150.         for (int i = 0; i < arr.length; i++) {
  151.             // i位置的数,我想随机和j位置的数做交换
  152.             int j = (int)(Math.random() * arr.length);// 0 ~ N-1
  153.             int tmp = arr[i];
  154.             arr[i] = arr[j];
  155.             arr[j] = tmp;
  156.         }
  157.         return arr; 
  158.     }
  161.     // [-range, +range]
  162.     public static int randomNumber(int range) {
  163.         return ((int)(Math.random() * range) + 1) - ((int)(Math.random() * range) + 1);
  164.     }
  167.     public static void main(String[] args) {
  168.         //int[] arr={4,3,1,3,3，1,1,4};
  169.         //int k=2;
  170.         //int m=3;
  171.         //System.out.println(onlyKTimes(arr, 2, 3));
  172.         // int kinds = 100;
  173.         int kinds = 4;
  174.         Lnt range = 200;
  175.         int testTime = 100000;
  176.         int max = 9;
  177.         System.out.print1n("测试开始");
  178.         for (int i = 0; i < testTime; i++) {
  179.             int a = (int)(Math.random() * max) + 1; //a 1~ 9
  180.             int b = (int)(Math.random() * max) + 1;//b1~9
  181.             // 让随机生成的两个数其中小的为k，大的为m
  182.             int k = Math.min(a, b);
  183.             int m = Math.max(a, b);
  184.             //k<m
  185.             if (k == m) {
  186.                 m++;    // 保证m比k大
  187.             }
  188.             int[] arr = randomArray(kinds, range, k, m);
  189.             int ans1 = test(arr, k, m);
  190.             int ans2 = onlyKTimes(arr, k, m);
  191.             if(ans1 != ans2) {
  192.                 System.out.println("出错了! ");
  193.             }
  194.         }
  195.         System.out.print1n("测试结束");
  196.     }
  197. }
  1. 用哈希表的方法时复杂度是O(n)，而用定义的长度为32的数组时复杂度为O(1)
  2. 通过对数器发现，上述代码中的onlyKTimesPlus方法在特殊情况时，仍旧有问题，边界情况仍需仔细考虑：
    1. 因为t二进制形式的数组初始化为全0，在遇到出现k次的数恰好是0时，就会出现问题；会造成0与其他出现m次的数据进行相同的处理（即continue忽略掉），会不断地触发continue===>因此会漏掉出现k次的刚好为0这种情况。
    2. 初始化为-1也不行，因为都是为1，这样或的时候就没有意义了；倒是可以考虑与0与一下，将能被m整除的位置上的和0与一下（随机应变===>实现同一种功能，代码有很多种写法）
  3. 有可能有的情况下就是写不出完美的代码的，就是需要打补丁才行！（虽然不好看，但是依然完成了任务）
  4. 解决方案：最后ans=0时检查一下，是不是0出现了k次（有更好的方式，单独遍历一回也没事）
  2. }
  3.  // 题目升级===>出现了k次就返回出现了k次的数，没有出现k次就返回-1
  4.     public static int onlyKTimesPlus(int[] arr, int k, int m) {
  5.         int[] t = new int[32];
  6.         // t[0] 0位置的1出现了几个
  7.         // t[i] i位置的1出现了几个
  8.         for (int num : arr) {
  9.             for(inti=0;i<=31;i++){
  10.                 t[i]+=(num>>i) & 1;
  11.             }
  12.         }
  13.         int ans = 0;
  14.         for(int i=0; i<32; i++){ 
  15.             // 题目升级===>出现了k次就返回出现了k次的数，没有出现k次就返回-1
  16.             if(t[i] % m == 0) {
  17.                 continue;
  18.             }
  19.             if(t[i] % m == k) {
  20.                 ans |= (1 << i);
  21.             }else {
  22.                 return -1;
  23.             }
  24.         }
  25.         if(ans == 0){
  26.             int count = 0;
  27.             for (int num : arr) {
  28.                 if(num == 0){
  29.                     count++ ;
  30.                 }
  31.             }
  32.             if (count != k)
  33.                 return -1;
  34.         }
  35.         return ans;
  36.     }

对数器能让你一看就知道哪错了（可以将出错的用例打印出来，方便调试与修改）

要复习、理解、写代码；要扩充题的！

左老师是个编剧