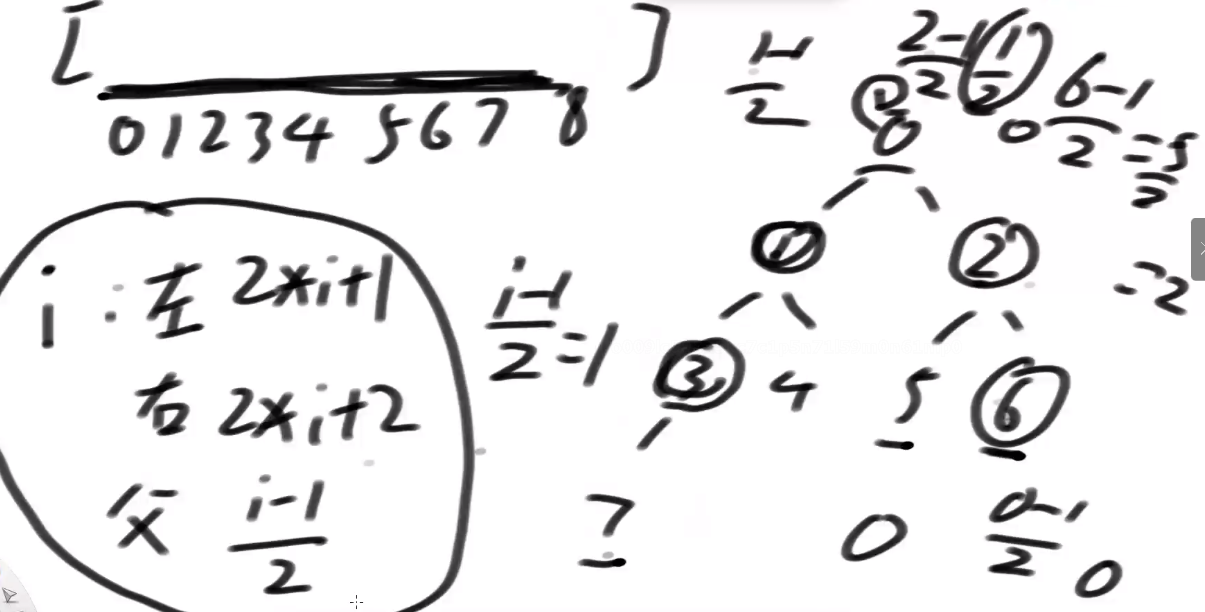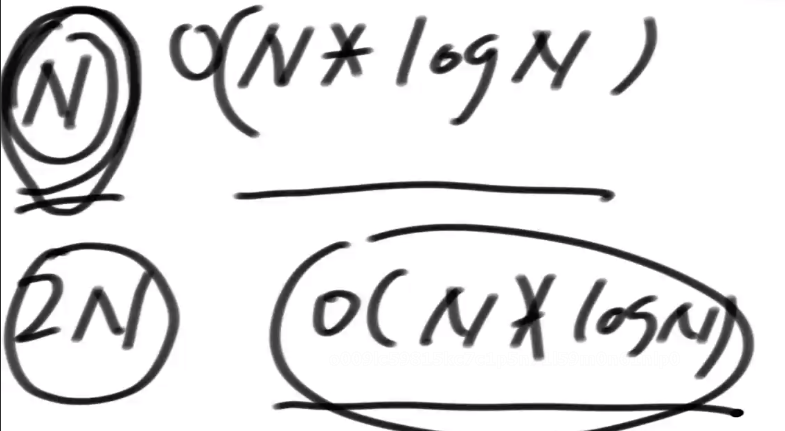比较器

比较器的本质就是重载比较运算符
比较器可以很好的应用在特殊标准的排序上
比较器可以很好的应用在根据特殊标准排序的结构.上
写代码变得异常容易，还用于范型编程
比如制定出自定义对象的比较规则
任何比较器：
1. compare方法里，遵循一个统一的规范：
  1. 返回负数的时候，认为第一个参数应该排在前面
  2. 返回正数的时候，认为第二个参数应该排在前面
  3. 返回0的时候，认为无所谓谁放前面
可以用在数组集合的排序上也可以用在有序表中
有序表中相同的key不会覆盖，而是直接忽略
lambda表达式中只有一条返回语句时，可以直接写要返回的内容

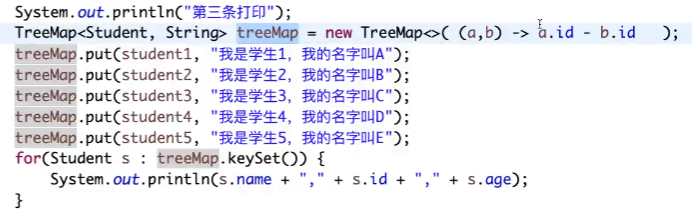
有序表中相同的key直接忽略，key是否相同取决于比较器的比较规则（假如是比较对象的id，id一样就说明一样，会忽略；而实际上这两个不是同一个对象！）
可以用对象的内存地址来进行比较

hashmap中的key为基本类型时会发生覆盖！

package class06;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Comparator;
import java.util.TreeMap;
public class Code01_Comparator {
    public static class Student {
        public String name;
        public int id;
        public int age;
        public Student(String name, int id, int age) {
            this.name = name;
            this.id = id;
            this.age = age;
        }
    }
    // 任何比较器：
    // compare方法里，遵循一个统一的规范：
    // 返回负数的时候，认为第一个参数应该排在前面
    // 返回正数的时候，认为第二个参数应该排在前面
    // 返回0的时候，认为无所谓谁放前面
    public static class IdShengAgeJiangOrder implements Comparator<Student> {
        // 根据id从小到大，但是如果id一样，按照年龄从大到小
        @Override
        public int compare(Student o1, Student o2) {
            return o1.id != o2.id ? (o1.id - o2.id) : (o2.age - o1.age);
        }
    }
    public static class IdAscendingComparator implements Comparator<Student> {
        // 返回负数的时候，第一个参数排在前面
        // 返回正数的时候，第二个参数排在前面
        // 返回0的时候，谁在前面无所谓
        @Override
        public int compare(Student o1, Student o2) {
            /*if(o1.id < o2.id) {
                return -1;
            } else if(o1.id > o2.id){
                return 1;
            } else {
                return 0;
            }*/
            return o1.id - o2.id;
        }
    }
    public static class IdDescendingComparator implements Comparator<Student> {
        @Override
        public int compare(Student o1, Student o2) {
            return o2.id - o1.id;
        }
    }
    // 先按照id排序，id小的，放前面；
    // id一样，age大的，前面；
    public static class IdInAgeDe implements Comparator<Student> {
        @Override
        public int compare(Student o1, Student o2) {
            return o1.id != o2.id ? o1.id - o2.id : (o2.age - o1.age);
        }
    }
    public static void printStudents(Student[] students) {
        for (Student student : students) {
            System.out.println("Name : " + student.name + ", Id : " + student.id + ", Age : " + student.age);
        }
    }
    public static void printArray(Integer[] arr) {
        if (arr == null) {
            return;
        }
        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i] + " ");
        }
        System.out.println();
    }
    public static class MyComp implements Comparator<Integer> {
        @Override
        public int compare(Integer o1, Integer o2) {
            return o2 - o1;
        }
    }
    public static class AComp implements Comparator<Integer> {
        // 如果返回负数，认为第一个参数应该拍在前面
        // 如果返回正数，认为第二个参数应该拍在前面
        // 如果返回0，认为谁放前面都行
        @Override
        public int compare(Integer arg0, Integer arg1) {
            return arg1 - arg0;
//            return 0;
        }
    }
    public static void main(String[] args) {
        Integer[] arr = { 5, 4, 3, 2, 7, 9, 1, 0 };
        Arrays.sort(arr, new AComp());
        for (int i = 0; i < arr.length; i++) {
            System.out.println(arr[i]);
        }
        System.out.println("===========================");
        Student student1 = new Student("A", 4, 40);
        Student student2 = new Student("B", 4, 21);
        Student student3 = new Student("C", 3, 12);
        Student student4 = new Student("D", 3, 62);
        Student student5 = new Student("E", 3, 42);
        // D E C A B
        Student[] students = new Student[] { student1, student2, student3, student4, student5 };
        System.out.println("第一条打印");
        Arrays.sort(students, new IdShengAgeJiangOrder());
        for (int i = 0; i < students.length; i++) {
            Student s = students[i];
            System.out.println(s.name + "," + s.id + "," + s.age);
        }
        System.out.println("第二条打印");
        ArrayList<Student> studentList = new ArrayList<>();
        studentList.add(student1);
        studentList.add(student2);
        studentList.add(student3);
        studentList.add(student4);
        studentList.add(student5);
        // N * logN
        studentList.sort(new IdShengAgeJiangOrder());
        for (int i = 0; i < studentList.size(); i++) {
            Student s = studentList.get(i);
            System.out.println(s.name + "," + s.id + "," + s.age);
        }
        // N * logN
        System.out.println("第三条打印");
        student1 = new Student("A", 4, 40);
        student2 = new Student("B", 4, 21);
        student3 = new Student("C", 4, 12);
        student4 = new Student("D", 4, 62);
        student5 = new Student("E", 4, 42);
        TreeMap<Student, String> treeMap = new TreeMap<>((a, b) -> (a.id - b.id));
        treeMap.put(student1, "我是学生1，我的名字叫A");
        treeMap.put(student2, "我是学生2，我的名字叫B");
        treeMap.put(student3, "我是学生3，我的名字叫C");
        treeMap.put(student4, "我是学生4，我的名字叫D");
        treeMap.put(student5, "我是学生5，我的名字叫E");
        for (Student s : treeMap.keySet()) {
            System.out.println(s.name + "," + s.id + "," + s.age);
        }
    }
}

完全二叉树

满的就是完全二叉树，不满也处在满的路上，而且是从左往右每一层依次变满的二叉树
空树是完全二叉树，只有根节点的也是完全二叉树，不能跳过左节点直接有右节点
表示完全二叉树：

经典的二叉树节点
从0 出发的一段连续的数组结构

任何i位置左孩子的位置在 2 * i + 1
任何i位置右孩子的位置在 2 * i + 2
任何i位置父节点的位置在（i - 1）/ 2
再加一个范围表示已经存在的大小

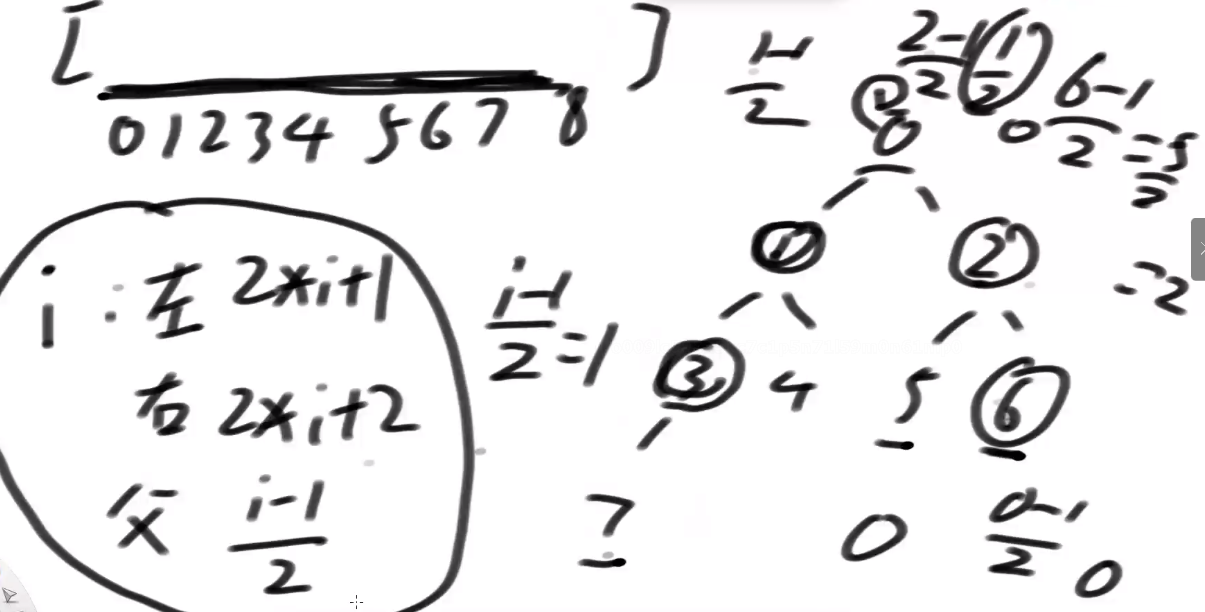
堆（优先队列）

堆是完全二叉树
大根堆：最大值为头部的值，每一棵子树都要满足这个（而不是整棵树中的最大值）
小根堆：最小值为头部的值，每一棵子树都要满足这个（而不是整棵树中的最大值）
任何一棵子树违规，那么他都不算堆了
不要左子树小于父节点，这是搜索二叉树，与堆无关
两个重要操作：heapinsert和heapify
系统中有现成的优先队列（PriorityQueue）===>默认是小根堆，基本类型可以不传比较器
中间有一个位置变化了，直接用heapinsert和heapify顺序调用，两个其实只发生一个（也可以互换顺序，两个只会发生一个，不发生的那个会进去检查，但是绝对不会出错）
堆结构中可以加重复值
复杂度：heapinsert和heapify都是O(logN)级别的（只与树的高度相关，最差沉到底是logN）

堆排序

给定一个无序数组，能不能调整成大根堆

整个数组中所有的数都调整成大根堆（假设一个一个给你）
将0位置的数与N-1位置的数做交换，最大值到N-1位置上了
将N-1位置断掉，size—
对新出现的换上来的顶部进行heapify
重复上述三个过程，直到size减为1（只剩一个数一定是排好序的）

复杂度为：O(N logN)（建堆是O(N logN)，互换再调整也是O(N logN)，加起来还是O(N logN)）
还有一种从下往上建堆的方法是O(N)的，但是堆排序仍突破不了O(N logN)，因为第二步（将大根堆的最顶上的元素换到最后在进行heapify）锁死了，不可能比O(N logN)之前更好
基于比较的排序中最好复杂度为O(N * logN)，有不基于比较的排序

分析复杂度

定性分析
增加数据量时，整个过程的复杂度是不是原来的那个

数据量波动的时候，怎么算复杂度===>开始的时候没有达到那么高的高度却以那么高的高度进行计算
用数据量增加常数法（N加倍即数据量加倍，复杂度是不会变化的）

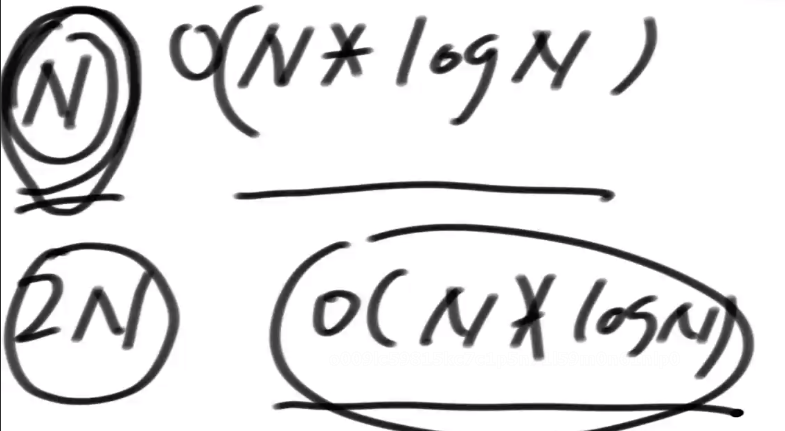
N logN是数据量为N时的上限，只要确定数据量为2N时的下限也是N logN即可
N * logN为什么是上限？因为有的没有那么高也算那么高了，以最坏情况估计logN
N * logN为什么是下限？因为2N时后一半的N一定有logN那么高了，以最好情况估计logN
夹逼===>数据量扩倍法（常用方法）

3. 从下往上建堆的方法===>O(N)

将之前无序的数组就看成是完全二叉树
将最底层的子树（叶结点）都用heapify调整成大根堆（向下沉调整成大根堆）
从下向上变成大根堆

具体实现上只要对数组从最后一个元素的位置进行heapify，遍历到位置0即可
❓最底层的数据最多，但是不用下沉，成本低了？？？

实质：

上->下：一个节点承担一层，两个节点承担两层，四个节点承担三层……

大量节点是高度增加之后加上去的，高度越高承担的节点越多

下->上：大量节点是层数少的，而少量的节点才是层数高的

用户一下子把数组给出才可以用从下往上，假如用户一个一个给你，只能从上向下（没办法一股脑去做）；而数组排序可以一下子把数组给你
堆排序中可以只含有heapify方法的，可以不要heapinsert
堆结构必须要有heapinsert
错位相减是计算技巧（分母一样，可以构成等比数列）===>幂级数收敛计算

附加题

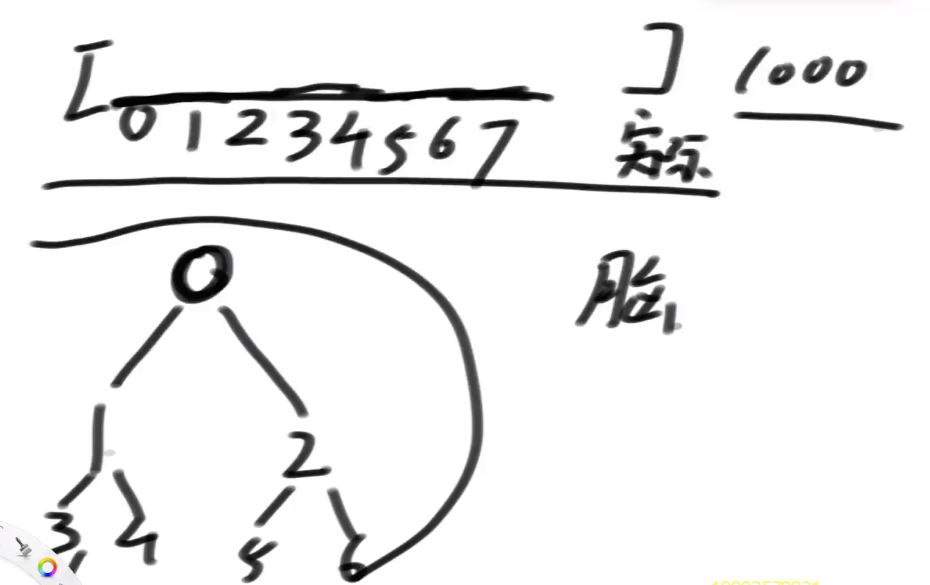
有一相对有序的数组（给出k，表示某一数与原来他应该所在的位置的的最大距离）
构建一个小根堆（先将数组中前k+1个数放到堆中去，小根堆最大为k+1），可以用系统实现的PriorityQueue
将小根堆中弹出的第一个数放到数组的0位置上去，一定是对的；并且将之前的后一个数也放到小根堆中去
弹出一个数放到1位置，再后一个数放到堆中去
………………（加一个弹一个）
复杂度：O(NlogK) ===>比O(NlogN)好
最后不够了，没法加了；只需要将栈弹空，把数组剩下的几个位置填满就完成了
额外空间复杂度是O(K+1)
解耦，先heapify，再heapinsert，不能将他们混合杂糅起来，那样太抽象了，写不出来

🤏随想

系统中的优先队列===>假如堆中一个元素的值发生了变化（甚至不知道是大了还是小了）===>从7位置开始看看能不能进行heapinsert（7），然后看看能不能进行heapify（7）；两个方法顺序调用，调用完成之后，整个堆就变成了正常的样子===>两个必然只执行一个！！！顺序调用两个其实只发生一个，也可以先2后1
系统中的优先队列默认是小根堆，可以通过定义比较器将其定义为大根堆（将比较器传到优先队列中去）
成员变量定义时初始化和之后初始化（构造器或者代码块）的区别https://blog.csdn.net/weixin_43271086/article/details/91470725

第一阶段

堆和堆排序

比较器

完全二叉树

堆（优先队列）

堆排序

分析复杂度

3. 从下往上建堆的方法===>O(N)

附加题

🤏随想