1. 评估算法优劣的核心指标是什么？
    1. 常数项时间（实现细节决定）
    2. 时间复杂度（流程决定）===>最大的核心指标，但是不是唯一的（有其他的指标）
      1. 常数时间的操作
      2. 确定算法流程的总操作数量与样本数量之间的表达式关系【写算法流程时一定要分解到小动作都是常数时间的，然后看看这些小动作的数量关系（求和、求承继、……）写出表达式来】
      3. 只看表达式的最高阶项的部分
    3. 额外空间复杂度（流程决定）
  2. 最重要的是时间复杂度，其次重要的是额外空间复杂度
  3. 递归的复杂度
  4. 左神github代码：github.com/algorithmzuo

常数操作（常数项?时间、常数时间）===>常数时间的操作

  • 固定时间的操作
  • 由实现细节决定
  • 与数值的大小、复杂程度无关
    • 1+1和1234+1234的计算复杂度一样
    • 寻址操作，数组寻址a[200w]和a[800w]一样（数组在逻辑上是连续的结构===>可以算出一个偏移量===>寻址虽然可能会有很少的跳转但是基本上时间是不变的，依然是常数操作）
      • 单链表不是固定时间操作，不是常数操作
  • 常见的常数时间的操作
    • 常见的算术运算（+、-、*、、、%等）
    • 常见的位运算（>>、>>>、<<、|、&、^等）
    • 赋值、比较、自增、自减操作等
    • 数组寻址操作
    • 执行时间是固定的操作都是常数时间的操作，时间不是固定的都不是常数时间的操作
    • 不是常数时间的操作必须分解为常数时间的操作，然后才可以去估计算法（不是常数时间还得往下分解）
      • 以for循环对单链表进行便利打印（使用get）为例===>O(n2)（也是迭代器比循环快、好、效率高的原因）

image.png

  1.   - 在链表中按顺序找到一个打印（“指针”后移一次O(1)，打印一次O(1)）===>总共O(n)

image.png

  • 感觉自己写的不错但是慢的原因：有可能写的某一条指令不是常数时间的操作（每一条指令都是常数时间的操作好一点），在分析时，没有分解为常数时间的操作，最终导致（时间复杂度）估计不准
  • 自己估流程必须保证每一个操作都是常数时间的操作，这样估计才准

时间复杂度

  1. 列出算法流程：在整个算法流程中，假设数据量为n，执行完整个流程，常数操作的数量是什么关系
  2. 如何确定算法流程的总操作数量与样本数量之间的表达式关系?
    1. 想象该算法流程所处理的数据状况，要按照最差情况来。
    2. 把整个流程彻底拆分为一个个基本动作，保证每个动作都是常数时间的操作。
    3. ❓如果数据量为N，看看基本动作的数量和N是什么关系。?===>按照表达式求和或者求乘积或者等差数列或者求别的（写出关于数据量的表达式—->复杂度表达式）
  3. 如何确定算法流程的时间复杂度?
    1. 当完成了表达式的建立，只要把最高阶项留下即可。低阶项都去掉,高阶项的系数也去掉。
    2. 记为: O(忽略掉系数的高阶项)
  4. 以选择排序为例：
    1. 第一次0~n-1中的最小值与0位置的数交换
      1. n个数看一遍（看n次），找最小值（n-1次比较）
      2. 最小值放到0位置 O(1）===>一次交换
    2. 第二次1~n-1中的最小值与1位置的数交换
      1. n-1个数看一遍（看n-1次），找最小值（n-2次比较）
      2. 最小值放到1位置 O(1）===>一次交换
    3. 第一次2~n-1中的最小值与2位置的数交换
    4. ……
  5. 估计时间复杂度列流程时，一定要精确到常数操作的流程（分解算法流程一定要分解到底）
  6. 不要默认某个算法步骤就是O(1)的，看清楚这个步骤是不是O(1)，拿捏不住必须搞清楚，不能略过，不然算复杂度会出错
  7. 上例选择排序中第一次看+比较n个常数项时间、第二次看+比较n-1个常数项时间、第三次看+比较n-2个常数项时间、……===>等差数列===>结果为an2+bn+c形式（a、b、c为常数）
  8. 上例选择排序中每一次交换的常数项时间均为1，所以加起来就为n
  9. 将5和6的结果加起来，依然可以写成an2+bn+c形式（a、b、c为常数）
  10. 表达式除了跟数据量有关之外，都是常数
  11. 复杂度：只要最高阶，并且前面的系数也不要===>O(n2)
  12. 复杂度只关心最高阶是什么！
  13. 估计得很粗糙，因为Big O定义的只要最高阶即可，所以可以粗糙一点
  14. 常数操作不受数据量影响，所以不用管常数操作
  15. 粗糙还有意义吗？
    1. 粗糙也有意义，一个三阶常数（项）小，一个二阶常数（项）很大，即便如此，在复杂度O(Big O) - 图3时，三阶必然比二阶大（此时只跟最高阶有关）（必然是发散的，只是看谁的发散速度快===>执行时间慢）
  16. 注意：
    1. 算法的过程，和具体的语言是无关的。
    2. 想分析一个算法流程的时间复杂度的前提，是对该流程非常熟悉
    3. 一定要确保在拆分算法流程时，拆分出来的所有行为都是常数时间的操作。这意味着你写算法时，对自己的用过的每一一个 系统api,都非常的熟悉。否则会影响你对时间复杂度的估算。
    4. 将O(n2)的看成O(1)估算会错！比如将冒泡排序看成1步……
  17. 时间复杂度的意义：
    1. 抹掉了好多东西，只剩下了一个最高阶项啊，那这个东西有什么意义呢?
    2. 时间复杂度的意义在于：
      1. 当我们要处理的样本量很大很大时，我们会发现低阶项是什么不是最重要的；每一项的系数是什么，不是最重要的。真正重要的就是最高阶项是什么。
      2. 这就是时间复杂度的意义，它是衡量算法流程的复杂程度的一种指标，该指标只与数据量有关，与过程之外的优化无关。

选择排序

  • 第一轮：从0开始找到最小值放到0位置
  • 第二轮：从1开始找到最小值放到1位置
  • 第三轮：从2开始找到最小值放到2位置
  • 第四轮：…… ```java package class01;

import java.util.Arrays;

public class Code01_SelectionSort {

  1. public static void selectionSort(int[] arr) {
  2.     if (arr == null || arr.length < 2) {
  3.         return;
  4.     }
  5.     // 0 ~ N-1
  6.     // 1~n-1
  7.     // 2
  8.     // 谁到n-1由外层循环的i控制
  9.     for (int i = 0; i < arr.length - 1; i++) { // i ~ N-1
  10.         // 最小值在哪个位置上  i～n-1
  11.         // 默认i位置是最小值的位置
  12.         int minIndex = i;
  13.         // 从i+1开始遍历找最小值（周而复始--->完成排序）
  14.         for (int j = i + 1; j < arr.length; j++) { // i ~ N-1 上找最小值的下标 
  15.             minIndex = arr[j] < arr[minIndex] ? j : minIndex;
  16.         }
  17.         swap(arr, i, minIndex);
  18.     }
  19. }
  21. public static void swap(int[] arr, int i, int j) {
  22.     int tmp = arr[i];
  23.     arr[i] = arr[j];
  24.     arr[j] = tmp;
  25. }
  27. // for test
  28. // Arrays工具类的排序方法
  29. public static void comparator(int[] arr) {
  30.     Arrays.sort(arr);
  31. }
  33. // for test
  34. // 生成随机数组
  35. public static int[] generateRandomArray(int maxSize, int maxValue) {
  36.     // Math.random()   [0,1)  
  37.     // Math.random() * N  [0,N)
  38.     // (int)(Math.random() * N)  [0, N-1]
  39.     int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
  40.     for (int i = 0; i < arr.length; i++) {
  41.         // [-? , +?]
  42.         arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
  43.     }
  44.     return arr;
  45. }
  47. // for test
  48. public static int[] copyArray(int[] arr) {
  49.     if (arr == null) {
  50.         return null;
  51.     }
  52.     int[] res = new int[arr.length];
  53.     for (int i = 0; i < arr.length; i++) {
  54.         res[i] = arr[i];
  55.     }
  56.     return res;
  57. }
  59. // for test
  60. // 为了测试两个排完序的数组是否一样
  61. public static boolean isEqual(int[] arr1, int[] arr2) {
  62.     if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
  63.         return false;
  64.     }
  65.     if (arr1 == null && arr2 == null) {
  66.         return true;
  67.     }
  68.     if (arr1.length != arr2.length) {
  69.         return false;
  70.     }
  71.     for (int i = 0; i < arr1.length; i++) {
  72.         if (arr1[i] != arr2[i]) {
  73.             return false;
  74.         }
  75.     }
  76.     return true;
  77. }
  79. // for test
  80. public static void printArray(int[] arr) {
  81.     if (arr == null) {
  82.         return;
  83.     }
  84.     for (int i = 0; i < arr.length; i++) {
  85.         System.out.print(arr[i] + " ");
  86.     }
  87.     System.out.println();
  88. }
  90. // for test
  91. public static void main(String[] args) {
  92.     int testTime = 500000;
  93.     int maxSize = 100;
  94.     int maxValue = 100;
  95.     boolean succeed = true;
  96.     for (int i = 0; i < testTime; i++) {
  97.         int[] arr1 = generateRandomArray(maxSize, maxValue);
  98.         int[] arr2 = copyArray(arr1);
  99.         selectionSort(arr1);
  100.         comparator(arr2);
  101.         if (!isEqual(arr1, arr2)) {
  102.             succeed = false;
  103.             printArray(arr1);
  104.             printArray(arr2);
  105.             break;
  106.         }
  107.     }
  108.     System.out.println(succeed ? "Nice!" : "Fucking fucked!");
  110.     int[] arr = generateRandomArray(maxSize, maxValue);
  111.     printArray(arr);
  112.     selectionSort(arr);
  113.     printArray(arr);
  114. }

}

  1. <a name="ItOcA"></a>
  2. ### 冒泡排序
  3. > 冒泡排序.
  4. > 过程:
  5. > 在arr[0 ~ N-1]范围上:
  6. > arr[0]和rr[1].谁大谁来到1位置; arr[1]和rr[2],谁大谁来到2位置-arr[N-2]和arr[N-1].谁大谁来到N-1位置
  7. > 在arr[0~N-2]范围上，重复上面的过程，但最后一步是arr[N-3]和arr[N-2].谁大谁来到N-2位置
  8. > 在arr[0~N-3]范围上，重复上面的过程，但最后-步是arr[N-4]和arr[N-3j,谁大谁来到N-3位置
  9. > 最后在arr[0~ 1]范围上，重复上面的过程，但最后-步是ar[0]和arr[1].谁大谁来到1位置
  10. > 估算:
  11. > 很明显，如果arr长度为N，每一步常数操作的数量，依然如等差数列一般
  12. > 所以，总的常数操作数量= a*(N^2)+ b+N+c(a、b、c都是常数)
  13. > 所以冒泡排序的时间复杂度为0(N^2)。
  15. - 第零个和第一个谁大谁跑到后面去（大的位于后面）
  16. - 第一个和第二个谁打谁往后
  17. - ……
  18. - 一轮下来最大的数就冒到最后去了===>冒泡排序名称的由来
  19. - n-1轮后排序完成
  20. - 复杂度要抹去很多东西===>模糊化处理
  21.    - n个O(1)
  22.    - n-1个O(1)
  23.    - n-2个O(1)
  24.    - ……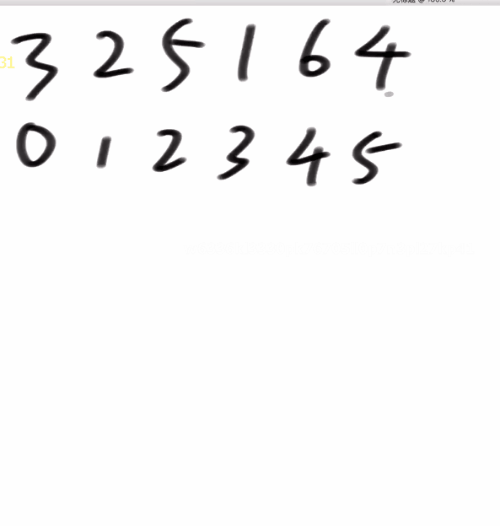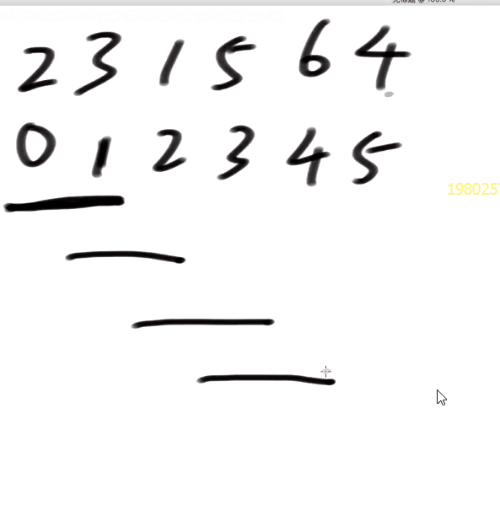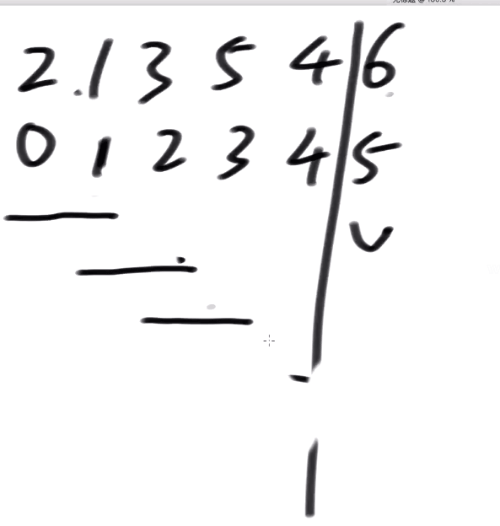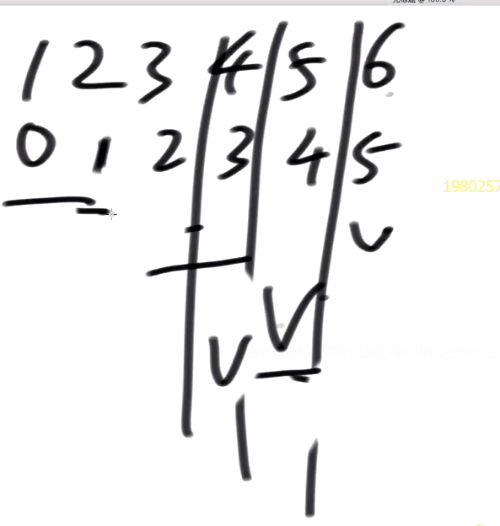
  25. - 等差感出来===>O(n2)
  27. ![冒泡排序2.gif](https://cdn.nlark.com/yuque/0/2021/gif/22850845/1633711064140-f453ce2b-b60f-4f88-9f3e-0223d9fa9d8c.gif#clientId=u48793030-b6a0-4&from=ui&id=u09ffa143&margin=%5Bobject%20Object%5D&name=%E5%86%92%E6%B3%A1%E6%8E%92%E5%BA%8F2.gif&originHeight=526&originWidth=500&originalType=binary&ratio=1&size=966022&status=done&style=none&taskId=u365834eb-d2e4-46ab-9695-7e2c8d36481)
  28. ```java
  29. package class01;
  31. import java.util.Arrays;
  33. public class Code02_BubbleSort {
  35.     public static void bubbleSort(int[] arr) {
  36.         if (arr == null || arr.length < 2) {
  37.             return;
  38.         }
  39.         // 0 ~ N-1
  40.         // 0 ~ N-2
  41.         // 0 ~ N-3
  42.         for (int e = arr.length - 1; e > 0; e--) { // 0 ~ e
  43.             for (int i = 0; i < e; i++) {
  44.                 if (arr[i] > arr[i + 1]) {
  45.                     swap(arr, i, i + 1);
  46.                 }
  47.             }
  48.         }
  49.     }
  51.     // 交换arr的i和j位置上的值
  52.     public static void swap(int[] arr, int i, int j) {
  53.         arr[i] = arr[i] ^ arr[j];
  54.         arr[j] = arr[i] ^ arr[j];
  55.         arr[i] = arr[i] ^ arr[j];
  56.     }
  58.     // for test
  59.     public static void comparator(int[] arr) {
  60.         Arrays.sort(arr);
  61.     }
  63.     // for test
  64.     public static int[] generateRandomArray(int maxSize, int maxValue) {
  65.         int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
  66.         for (int i = 0; i < arr.length; i++) {
  67.             arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
  68.         }
  69.         return arr;
  70.     }
  72.     // for test
  73.     public static int[] copyArray(int[] arr) {
  74.         if (arr == null) {
  75.             return null;
  76.         }
  77.         int[] res = new int[arr.length];
  78.         for (int i = 0; i < arr.length; i++) {
  79.             res[i] = arr[i];
  80.         }
  81.         return res;
  82.     }
  84.     // for test
  85.     public static boolean isEqual(int[] arr1, int[] arr2) {
  86.         if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
  87.             return false;
  88.         }
  89.         if (arr1 == null && arr2 == null) {
  90.             return true;
  91.         }
  92.         if (arr1.length != arr2.length) {
  93.             return false;
  94.         }
  95.         for (int i = 0; i < arr1.length; i++) {
  96.             if (arr1[i] != arr2[i]) {
  97.                 return false;
  98.             }
  99.         }
  100.         return true;
  101.     }
  103.     // for test
  104.     public static void printArray(int[] arr) {
  105.         if (arr == null) {
  106.             return;
  107.         }
  108.         for (int i = 0; i < arr.length; i++) {
  109.             System.out.print(arr[i] + " ");
  110.         }
  111.         System.out.println();
  112.     }
  114.     // for test
  115.     public static void main(String[] args) {        
  116.         int testTime = 500000;
  117.         int maxSize = 100;
  118.         int maxValue = 100;
  119.         boolean succeed = true;
  120.         for (int i = 0; i < testTime; i++) {
  121.             int[] arr1 = generateRandomArray(maxSize, maxValue);
  122.             int[] arr2 = copyArray(arr1);
  123.             bubbleSort(arr1);
  124.             comparator(arr2);
  125.             if (!isEqual(arr1, arr2)) {
  126.                 succeed = false;
  127.                 break;
  128.             }
  129.         }
  130.         System.out.println(succeed ? "Nice!" : "Fucking fucked!");
  132.         int[] arr = generateRandomArray(maxSize, maxValue);
  133.         printArray(arr);
  134.         bubbleSort(arr);
  135.         printArray(arr);
  136.     }
  138. }

插入排序

插入排序 过程: 想让arr[0~0]上有序，这个范围只有一个数，当然是有序的。 想让r[(0~1]上有序，所以从arr[1]开始往前看， 如果arr[1]<arr[0]I. 就交换。否则什么也不做。 想让arr[0~i]上有序，所以从arrQ]开 始往前看，ar[]这个数不停向左移动，-直移动到左边的数字不再比 自己大，停止移动。 最后-步，想让arr[0-N-1]上有序，arr[N- 1]这个数不停向左移动，一 直移动到左边的数字不再比自己 大，停止移动。 估算时发现这个算法流程的复杂程度，会因为数据状况的不同而不同。

如果某个算法流程的复杂程度会根据数据状况的不同而不同，那么你必须要按照最差情况来估计。 很明显，在最差情况下，如果arr长度 为N,插入排序的每一步常 数操作的数量，还是如等差数列- -般 所以，总的常数操作数量= a(N^2) + bN+c(a、b. c都是常数) 所以插入排序排序的时间复杂度为0(N^2)。

  • 使0~0上有序
  • 使0~1上有序，盯着1位置往前看，假如比前面的数小交换，再往前看，直到前面没有数了或者前面的数不比当前的数（最初时的最后一个数）大了
  • 使0~2上有序
  • ……
  • 使0~n-1上有序
  • 完成排序
  • 插入排序分好几种===>希尔排序调整步长的插入排序（这里是经典的插入排序 ）
  • 当数据状况会影响时间复杂度时，按最坏的数据状况来估计时间复杂度===>事实上Big O就是最坏情况下的时间复杂度（Ω是平均下的时间复杂度，复杂度O(Big O) - 图4是最好情况下的时间复杂度）===>不做学术不要管（渐近紧上界）
  • 类似打牌时摸牌从最后插入到合适的顺序的位置
  • 与冒泡排序区别很大，冒泡排序不管数据状况，即使在很有序的情况下也很固定，每次都要比较只是不要交换；虽然不用交换，但比较的次数没有少，按表达式算最高阶依然是n2；在数据状况很好的情况下依然为===>O(n2)

插入排序4-min.gif

  1. package class01;
  3. import java.util.Arrays;
  5. public class Code03_InsertionSort {
  7.     public static void insertionSort(int[] arr) {
  8.         if (arr == null || arr.length < 2) {
  9.             return;
  10.         }
  11.         // 0~0 有序的
  12.         // 0~1 有序的
  13.         // ……
  14.         // 0~i 想有序
  15.         // 0~n-1有序
  16.         for (int i = 1; i < arr.length; i++) { // 0 ~ i 做到有序
  17.             for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
  18.                 // j+1永远是我们盯着的那个数（新要排序的数）
  19.                 // j为j+1左边的数
  20.                 swap(arr, j, j + 1);
  21.             }
  22.         }
  23.     }
  25.     // i和j是一个位置的话，会出错
  26.     // 通过异或运算交换两个数 
  27.     // 位运算速度快
  28.     public static void swap(int[] arr, int i, int j) {
  29.         arr[i] = arr[i] ^ arr[j];
  30.         arr[j] = arr[i] ^ arr[j];
  31.         arr[i] = arr[i] ^ arr[j];
  32.     }
  34.     // for test
  35.     public static void comparator(int[] arr) {
  36.         Arrays.sort(arr);
  37.     }
  39.     // for test
  40.     public static int[] generateRandomArray(int maxSize, int maxValue) {
  41.         // Math.random() ->  [0,1) 所有的小数，等概率返回一个
  42.         // Math.random() * N -> [0,N) 所有小数，等概率返回一个
  43.         // (int)(Math.random() * N) -> [0,N-1] 所有的整数，等概率返回一个
  44.         int[] arr = new int[(int) ((maxSize + 1) * Math.random())]; // 长度随机 
  45.         for (int i = 0; i < arr.length; i++) {
  46.             arr[i] = (int) ((maxValue + 1) * Math.random()) 
  47.                     - (int) (maxValue * Math.random());
  48.         }
  49.         return arr;
  50.     }
  52.     // for test
  53.     public static int[] copyArray(int[] arr) {
  54.         if (arr == null) {
  55.             return null;
  56.         }
  57.         int[] res = new int[arr.length];
  58.         for (int i = 0; i < arr.length; i++) {
  59.             res[i] = arr[i];
  60.         }
  61.         return res;
  62.     }
  64.     // for test
  65.     public static boolean isEqual(int[] arr1, int[] arr2) {
  66.         if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
  67.             return false;
  68.         }
  69.         if (arr1 == null && arr2 == null) {
  70.             return true;
  71.         }
  72.         if (arr1.length != arr2.length) {
  73.             return false;
  74.         }
  75.         for (int i = 0; i < arr1.length; i++) {
  76.             if (arr1[i] != arr2[i]) {
  77.                 return false;
  78.             }
  79.         }
  80.         return true;
  81.     }
  83.     // for test
  84.     public static void printArray(int[] arr) {
  85.         if (arr == null) {
  86.             return;
  87.         }
  88.         for (int i = 0; i < arr.length; i++) {
  89.             System.out.print(arr[i] + " ");
  90.         }
  91.         System.out.println();
  92.     }
  94.     // for test
  95.     public static void main(String[] args) {
  96.         int testTime = 500000;
  97.         int maxSize = 100; // 随机数组的长度0～100
  98.         int maxValue = 100;// 值：-100～100
  99.         boolean succeed = true;
  100.         for (int i = 0; i < testTime; i++) {
  101.             int[] arr1 = generateRandomArray(maxSize, maxValue);
  102.             int[] arr2 = copyArray(arr1);
  103.             insertionSort(arr1);
  104.             comparator(arr2);
  105.             if (!isEqual(arr1, arr2)) {
  106.                 // 打印arr1
  107.                 // 打印arr2
  108.                 succeed = false;
  109.                 break;
  110.             }
  111.         }
  112.         System.out.println(succeed ? "Nice!" : "Fucking fucked!");
  114.         int[] arr = generateRandomArray(maxSize, maxValue);
  115.         printArray(arr);
  116.         insertionSort(arr);
  117.         printArray(arr);
  118.     }
  120. }

额外空间复杂度

  1. 你要实现一个算法流程，在实现算法流程的过程中，你需要开辟一些空间来支持你的算法流程。
  2. 作为输入参数的空间，不算额外空间。（用户给你的东西不算做额外空间）（参数）
  3. 作为输出结果的空间，也不算额外空间。（用户要求返回的东西也不算额外空间）（返回值）return new int[n];—->不算额外空间
  4. 要实现算法构造的辅助数组就算额外空间了！
  5. 程序员自主空间，和用户无关的空间
  6. 因为这些都是必要的、和现实目标有关的。所以都不算。
  7. 但除此之外，你的流程如果还需要开辟空间才能让你的流程继续下去。
  8. 这部分空间就是额外空间。
  9. 如果你的流程只需要开辟**有限几个变量**，额外空间复杂度就是0(1)。===>常数（项）空间的额外空间
  10. 也要按照最坏情况估计
  11. 例子：求出现次数最多的数字===>用hashmap统计（最坏情况n—->O(n)）；字母表法也行（用数组存，数字作为下标，数组值作为个数）

算法流程的常数项(与最开始的常数操作的常数时间是不一样的)

  1. 这里是指算的时间复杂度的表达式的常数项之间进行比较（插入比冒泡好，在某些情况下插入排序更好）
  2. O(n)实现的再丑再冗余也比O(n2)好
  3. 但是两个算法的时间复杂度一样的时候就要进入拼常数时间的阶段了
  4. 简称拼常数项
  5. 比拼方式：实测
    1. 放弃理论分析，生成随机数据直接测。
    2. 为什么不去理论分析?（不需要理论，因为用理论很难估计）
      1. 不是不能纯分析，而是没必要。因为不同常数时间的操作，虽然都是固定时间，但还是有快慢之分的。
      2. 比如，位运算的常数时间原小于算术运算的常数时间，这两个运算的常数时间又远小于数组寻址的时间。（+<^;/<+;……）（都是常数时间但是有的快有的慢）
    3. 所以如果纯理论分析，往往会需要非常多的分析过程。都已经到了具体细节的程度，莫不如交给实验数据好了。
  6. 面试、比赛、刷题中，一个问题的最优解是什么意思?
    1. 时间复杂度尽可能低
    2. 在a基础上空间复杂度尽可能低（优化），在最低时间复杂度的基础上尽可能地优化空间复杂度
    3. 不包括常数优化（面试或比赛时不会卡常数时间的，样本只要你时间和空间复杂度做到即可）
    4. 做题时不用管（比如用异或代替加法更优，这是实现上的优化细节，可以不用管）
    5. 仁者见仁，智者见智（常数时间加分，常数时间在最优解之外===>只比最高项）
    6. 一般情况下，认为解决一个问题的算法流程，在时间复杂度的指标上，一定要尽可能的低，先满足了时间复杂度最低这个指标之后，使用最少的空间的算法流程，叫这个问题的最优解。一般说起最优解都是忽略掉常数项这个因素的，因为这个因素只决定了实现层次的优化和考虑，而和怎么解决整个问题的思想无关。

常见时间复杂度的排名

常见的时间复杂度: 排名从好到差: O(1)===>3+5 O(logN) O(N) O(N*logN) O(N^2) O(N^3) …… O(N^K) O(2^N) O(3^N) …… O(K^N)===》递归决策，递归有多条分支的情况下有可能出现这种复杂度 O(N!)

递归的复杂度（时间、空间）

见之后的题目专题……

算法和数据结构学习的大脉络

  1. 知道怎么算的算法(流程规定的特别精确，不管什么数据流程都被规定好了，明确知道怎么去算===>3+5、5+6)
  2. 知道怎么试的算法（最重要的）（图灵祖师爷===>奠定了怎么试的算法）
  3. 两种类型在面试中一半一半对半开！
  4. 我们所有的题目讲解，对于大脉络的实践贯穿始终

数学知识

🌟排列组合 等差数列

🤏随想

  1. 排序一般从小到大
  2. 从大到小一般为逆序