加强堆

最大线段重合问题（用堆的实现）

给定很多线段，每个线段都有两个数组[start, end]，表示线段开始位置和结束位置，左右都是闭区间 规定: 1)线段的开始和结束位置一定都是整数值 2)线段重合区域的长度必须>=1 返回线段最多重合区域中，包含了几条线段

敏感度问题：学了东西之后，遇到题目，想不到用什么东西解的===>只能通过练习来搞定（系统学习班中有大量的题，实战会在刷题班）

1. 笨方法
   1. 求出所有线段中最小的开始位置和最大的结束位置
   2. 遍历最小与最大之间的.5，分别看有多少线段包含这些.5的
   3. 最终的答案在b中的结果中，即所有答案中的最大值
   4. 因为由题意，重叠区域必包含.5（可以拿.1、.2、……但是不能用整数点统计，因为那样可能不包含重叠区域）

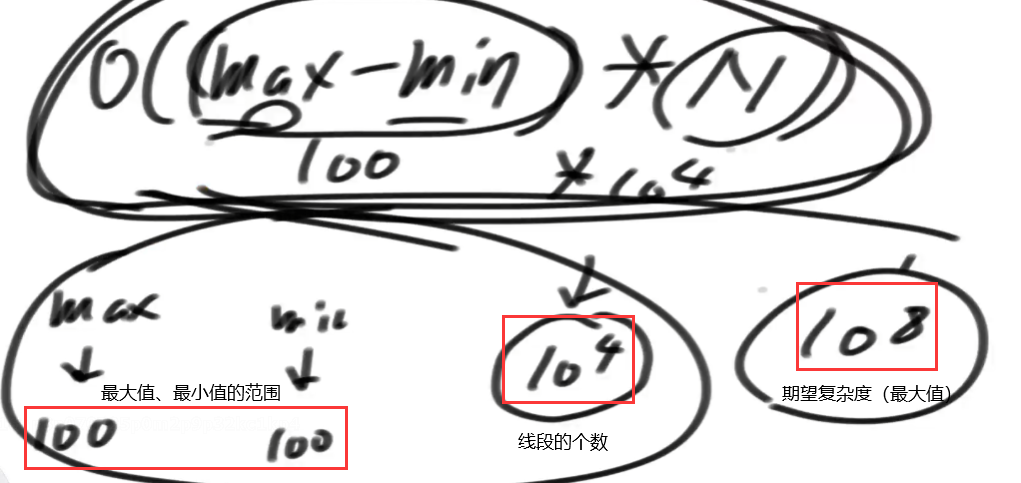
1. 复杂度：（max-min）个.5，每一个.5都需要遍历
   1. O((max-min)*N)

1. 好的办法
   1. 根据每一线段开始位置排序，可以用比较器
   2. 准备小根堆（最小的值放在根节点）
   3. 遍历每一个线段===>将小根堆中≤线段左端点的值弹出
   4. 弹出之后再把c中线段结尾的值放入堆中
   5. 此时小根堆中有几个数就是答案
   6. 重复上述d、e，求出所有线段所对应的答案
   7. 最终的答案为f中最大的值
   8. 为什么用小根堆：因为小根堆调整快（依次弹出/加进去小的在最上面）
2. 结论：
   1. 任何一个重合区域，所有线段不管是什么成分，只要是重合区域，这个重合区域的左边界必是某个线段的左边界
   2. 考察每一个线段的左边界，假设他是重合区域的左边界，求出该左边界向右的最大贯数量就是答案
   3. b中的贯穿数量是以当前左边界为开始，看小根堆中（即之前的左边界在当前的左边界左边的线段）的右边界是否能够贯穿当前的左边界===>求出的数量就是以此左边界为左边界的重合区域的数量
3. 为什么左边界相同的线段，有边界换顺序不影响结果？
   1. 因为反正都要求的
   2. 先出现后出现都没有关系（完全没关系）
   3. 同样左边界的线段先计算的线段的有边界在之后计算相同左边界的线段的时候绝对不会弹出，因此会将这条线段算进去，最终还是计算了，所以不会有影响
   4. 因为求max，不会有影响
   5. 该出去的迟早要出去？？？

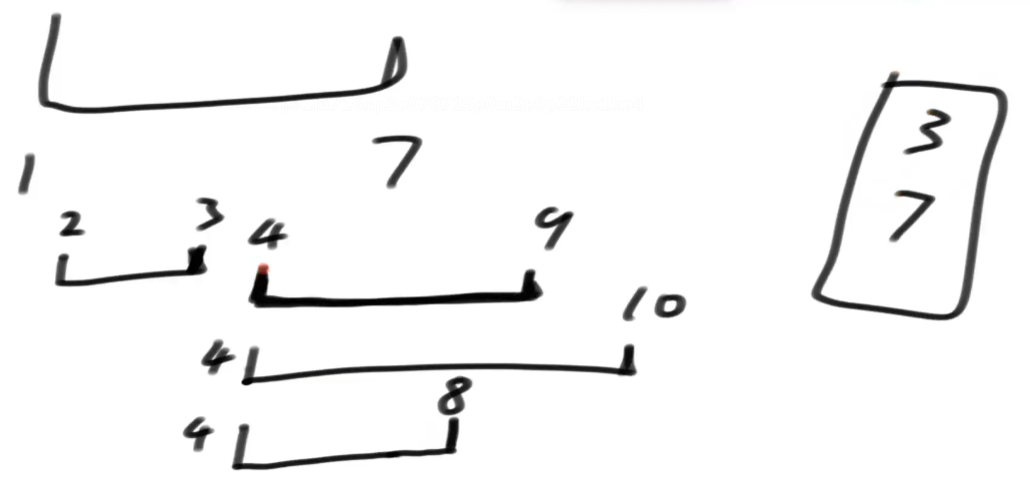
1. 执行到某一步时，之前的线段都是全了的，而不影响的线段都是弹出去的，留下的必然是满足条件（能够贯穿、会影响的）的线段
2. 整个问题就是一种贪心的思想===>贪心策略的证明（必要的）===>这题不难证
3. 复杂度：O(N*logN)===>虽然有两层循环，但是对于每一个线段都只进一次堆，并且只出一次堆，总共2N次，而每一次进堆和出堆调整的时候都是O(logN)；而且还有排序的O(NlogN)；以及初始化一些操作

4. 最差情况：每次都需要从底向上换，复杂度为O(logN)，而不是O(1)

   手动改写堆(非常重要) !

   系统提供的堆（PriorityQueue）无法做到的事情: 1)已经入堆的元素，如果参与排序的指标方法变化，系统提供的堆无法做到时间复杂度O(logN)调整! 都是O(N)的调整! 2)系统提供的堆只能弹出堆顶，做不到自由删除任何一个堆中的元素，或者说，无法在时间复杂度O(logN)内完成!一定 会高于O(logN) 根本原因：无反向索引表

5. 排在堆中数据的属性发生了变化：此时该节点要发生相应的移动===>系统提供的堆不支持这样的改动

6. 对于系统的堆，该了一个字段之后，这个堆就属于无效堆了，因为系统中的堆不知道你哪改了哪没改
7. 系统实现的堆无法高效地调整好===>没有反向索引表
8. 数组本身就是一张索引表===>即0位置上放的是什么，1位置上放的是什么……
9. 但是没有没有某一元素放在哪的反向索引表
10. 假如将b改变了，都知道要将b移动，但是不知道b在哪；只能遍历找到b的位置，找到b后才能看能不能往上或者往下做调整，至少为O(N)===>假如有反向索引表，那么可以直接查，再去调整就是O(logN)的代价
11. 系统没有反向索引表，只能自己手写===>PriorityQueue的底层源码===>没有反向索引表===>没法高效地做到以O(logN)更新堆中的某一个元素！（也可以做到，但是复杂度高O(N)，要去遍历找修改点的位置）
12. 各种语言有各种语言的特点===>java语言偏应用，一般堆的应用就是加入和弹出，这样就能满足需求了（面对这样一个简单的场景没有增加反向索引的动力），假如再加一个反向索引表就需要维护还要费内存===>c++的委员会可能会提供这样的包，虽然也不在c++原生库中===>有的语言有反向索引表，有的语言有
13. 加强堆仍然能够有重复值===>在比较器中，如果内部的值一样，那么对内存地址也做比较就行了===>这种处理方法可能是有序表中的处理方法===>而优先队列或者加强堆中是在heapinsert和heapify中进行了特殊处理才使相同值得对象可以同时存在的！！！
14. peek等边界判断（堆中有没有元素）交给用户去判断
15. ❓拿地址和他的值一起来参与比较！？？？===>就不会被覆盖掉
16. T一定是要非基础类型===>因为hashmap不认比较器，它里面传的基本类型的key会自动将其覆盖掉===>即使其他的结构可以认相同的值，但是用hashmap实现的反向索引表不认这个
17. 前面一个视频中提到了一个对象的内存地址进行比较！

1. 对于上面的问题，可以考虑包一层（包装一下）
2. 包一层之后就有自己的内存地址了！！！（基础类型可能因为缓存的原因没有自己的内存地址）
3. 包装的那个类Inner只有自己可见，只要是为了绕基本类型的值传递

1. heapify和heapinsert绝对只会发生一个！！！？？？上节课
2. 中间值变化过程与remove掉一个中间值的过程
3. heapinsert向上；heapify向下
4. 没有删掉子树这个概念（因为堆必然是完全二叉树）
5. 边界情况：最后一个元素就是我们要删除的元素

模拟抽奖系统（候选区、得奖区）

1. 暴力：两个堆倒来倒去===>业务搞清楚，先模拟出这个过程（流程），不用任何优化（之后看有什么问题再去优化他）

数据量大小、长度、值的范围等===>推测写什么样的算法能过

c++：1~2s
java：2~4s
表示代码的指令条数在108~109以内
一般这么多以内即可（结论）
不写代码就知道能不能过
数组长度为103，假如想出一个O(N2)的算法一定能过===>可以通过这种方法反推需要什么算法
不管什么样的oj都不会差太大的数量级===>cpu是线性增长的
算法题不可能多线程去跑！都是单线程！
如下算法复杂度只与N有关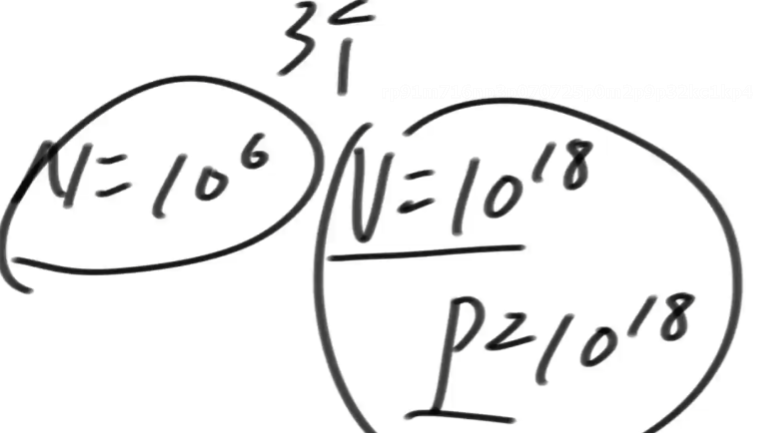

牛课上有这种范围，leetcode上没有
O(1)就是一条指令
空间复杂度也会有上限

笔试中可以通过数据量或者其他的一些时间限制或空间复杂度来推断该算法题中使用的方法
面试中要尽量用最优解去解，更考察思维轨迹，面试官可能调范围，让你想别的算法
面试更灵活
面试的算法题没有笔试出现的题难（笔试中的最后两道题不是给一般人做的，一般是给比赛的人做的）
前面的题做的很好，最后两道题也做出来了，会发ssp
谷歌的传统
facebook最初的六道题（做出一道就可以面试），只招三种人：谷歌退下来的、名校毕业、员工只能推荐一个人

🤏随想

Math.max的复杂度是O(1)的

ArrayList的set和get是O(1)，虽然有扩容，但仍是O(1)

包装模式？？？===>外观模式就是门面模式Facade

学东西不能觉得这样有道理就行，不要不在意，一定要放在心上===>记住！！！

要会自己造轮子才行！！！！