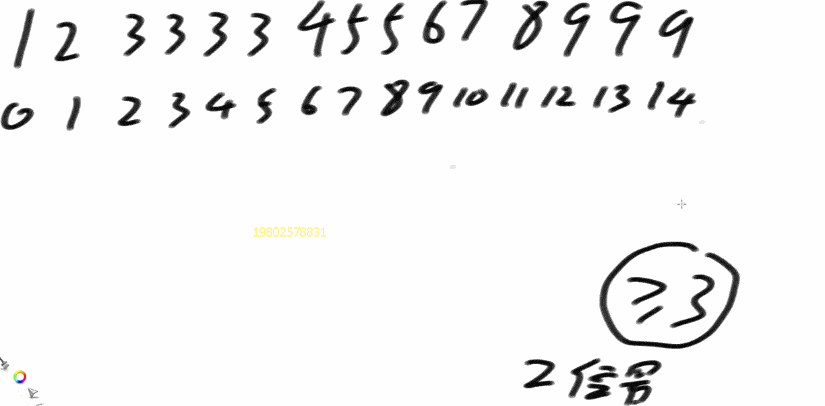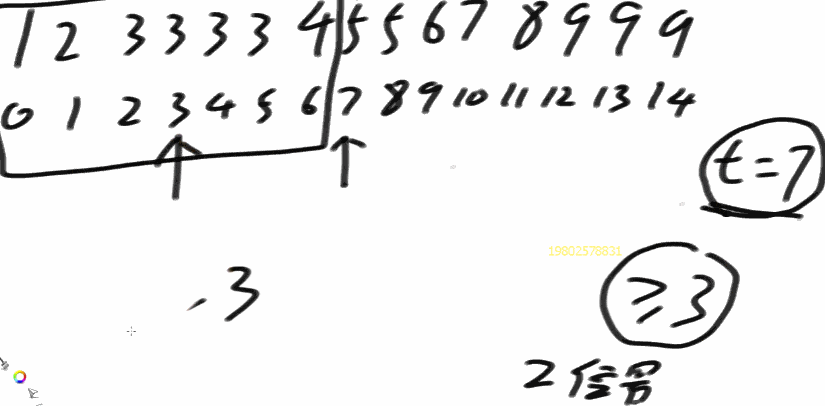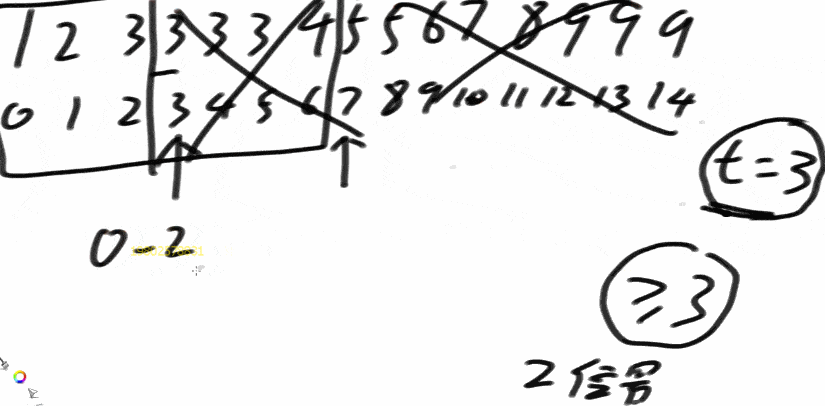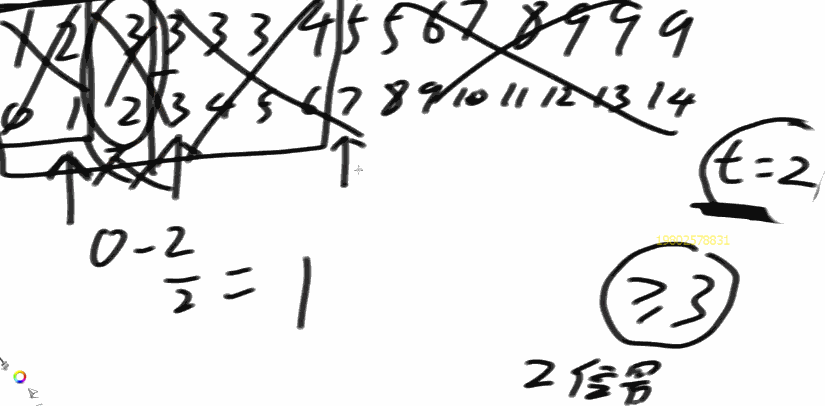1. 经常见到的类型是在一个有序数组上,开展二分搜索，但有序真的是所有问题求解时使用二分的必要条件吗？
  1. 不

，只要能正确构建左右两侧的淘汰逻辑，你就可以二分**。**

  1. 边界条件需要注意，可能会写出错的边界
  2. 经典案例：二分法查找值===>有序，一次砍一半
  3. 复杂度：O(log2N)===>一次砍一半，一共砍log2N次，每找到一次看一眼决定怎么砍的都是O(1)的
  4. 以10为底lg，以e为底ln，以2为底log，以其他为底logx
  5. 长度非2的整次方时也是O(log2N)，因为复杂度忽略常数项……
  6. 有序的一定能二分，无序的也有可能能二分

经典题型

  1. 在一个有序数组中，找某个数是否存在
  2. 在一个有序数组中，找>=某个数最左侧的位置
    1. 二分到最后，一定是到没有数的
    2. 砍一半，砍掉的一半知道是否满足条件，但是另一半不知道
    3. 一定会二分到死，到最后，在这过程中用一变量记录着出现的答案，最后一和答案就是最终答案
  3. 在一个有序数组中，找<=某个数最右侧的位置
  4. 局部最小值问题
    1. 无序数组（包含正负和0）
    2. 任意相邻的数不相等
    3. 0位置只要小于1位置就是局部最小
    4. n-1位置只要小于n-2位置就是局部最小
    5. 其他位置n不仅要比n-1小还要比n+1小才是局部最小
    6. 在无序数组中只要找到这样一个局部最小就行（不管哪一个、有多少），只要找一个局部最小的位置即可，返回一个即可（不管返回哪一个）
  5. 二分不一定要有序才能二分（见4）
    1. 数据状况特殊的情况
    2. 问的问题本身很特殊—->局部极小值
    3. 满足上述两个条件可能有特殊的优化
    4. 优化角度
      1. 数据本身
      2. 问的问题
    5. 只要构建一种排他性的策略，左右两侧有一半肯定有，另一半可能有或可能没有，将那一半不确定的砍掉即可，留下肯定有的那一半
    6. 只要能构建排他性的条件（东西），不一定数组有序，题目就能二分！
  6. 二分的循环条件中是小于的时候表示至少要两个数（最后一次left等于了right，所以最后还要判断left是不是满足条件或者直接返回left；注意：放缩即左右选取是在while循环体内进行的，通过判断选择砍哪一半，直到最后砍到只剩一个元素为止直接跳出，而下面一种方式是将最后一个元素依然包括在循环体内判断然后直接返回的），二分的循环条件中是小于等于的时候表示至少一个数（这时所有的判断都在while循环以内，直接return结果）

一个有序数组中，找某个数是否存在

  1. package class01;
  3. public class Code04_BSExist {
  5.     public static boolean exist(int[] sortedArr, int num) {
  6.         if (sortedArr == null || sortedArr.length == 0) {
  7.             return false;
  8.         }
  9.         int L = 0;
  10.         int R = sortedArr.length - 1;
  11.         int mid = 0;
  12.         // L..R
  13.         // L~R上至少有两个数时才进行二分，所以退出的时候可能还有一个数没有验，所以要把这最后一个数验一下
  14.         while (L < R) {
  15.             // mid = (L+R) / 2;
  16.             // L 10亿  R 18亿
  17.             // 数值太大了会造成溢出，会出错！、
  18.             // 使用这种写法可以避免溢出
  19.             // 相减不会溢出，除以更不会溢出；并且R没有溢出，加上相减的一半也不会溢出
  20.             // l/2+r/2应该也可以，但两次除效率低；在都是奇数的情况下要处理好===>边界条件调整好可以搞
  21.             // l/2不是裸的l/2，出来后可能要加工一下（加1、减1这样）
  22.             // N/2 = N>>1（带符号右移）
  23.             // 位运算比除法、乘法快
  24.             // 能优化一点小常数就优化一点小常数
  25.             // mid = L + (R - L) / 2
  26.             // N / 2    N >> 1
  27.             mid = L + ((R - L) >> 1); // mid = (L + R) / 2
  28.             if (sortedArr[mid] == num) {
  29.                 return true;
  30.             } else if (sortedArr[mid] > num) {
  31.                 R = mid - 1;
  32.             } else {
  33.                 L = mid + 1;
  34.             }
  35.         }
  36.         // L~R上至少有两个数时才进行二分，所以退出的时候可能还有一个数没有验，所以要把这最后一个数验一下
  37.         // while (L < R) {}都对，只不过这两种情况下逻辑的边界条件不一样===>处理方式不一样但都对
  38.         // 边界条件必不可少，仁者见仁智者见智
  39.         return sortedArr[L] == num;
  40.     }
  42. }

在一个有序数组中，找>=某个数最左侧的位置

  1. 二分到最后，二分到没有数的
  2. 图中t为最终答案，所以当中间位置不是大于等于3的时候，t不更新
  3. t是用来记录答案的，与mid中间位置无关！！！
  4. 思路二分：看mid所对应的数是不是大于等于那个数的
    1. 假如大于等于，记录下这时的mid，并且砍掉右半部分，留下左半部分，进行下一次二分，直到L>R
    2. 假如小于，保存最终答案的那个变量不更新，砍掉左半部分，留下右半部分，进行下一次二分，直到L>R
    3. 最终结果保存在变量t中

二分找大于等于某个数最左侧的位置1-min.gif

  1. package class01;
  3. import java.util.Arrays;
  5. public class Code05_BSNearLeft {
  7.     // 在arr上，找满足>=value的最左位置
  8.     public static int nearestIndex(int[] arr, int value) {
  9.         int L = 0;
  10.         int R = arr.length - 1;
  11.         int index = -1; // 记录最左的对号
  12.         // 至少一个数时可以二分（注意边界条件）
  13.         while (L <= R) {
  14.             // 只剩一个数时，算mid的时候仍然是mid=L=R（此时L或者R无论是谁再变化一下都会造成L>R跳出循环）
  15.             int mid = L + ((R - L) >> 1);
  16.             if (arr[mid] >= value) {
  17.                 index = mid;
  18.                 R = mid - 1;
  19.             } else {
  20.                 L = mid + 1;
  21.             }
  22.         }
  23.         // 返回结果
  24.         return index;
  25.     }
  27.     // for test
  28.     public static int test(int[] arr, int value) {
  29.         for (int i = 0; i < arr.length; i++) {
  30.             if (arr[i] >= value) {
  31.                 return i;
  32.             }
  33.         }
  34.         return -1;
  35.     }
  37.     // for test
  38.     public static int[] generateRandomArray(int maxSize, int maxValue) {
  39.         int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
  40.         for (int i = 0; i < arr.length; i++) {
  41.             arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
  42.         }
  43.         return arr;
  44.     }
  46.     // for test
  47.     public static void printArray(int[] arr) {
  48.         if (arr == null) {
  49.             return;
  50.         }
  51.         for (int i = 0; i < arr.length; i++) {
  52.             System.out.print(arr[i] + " ");
  53.         }
  54.         System.out.println();
  55.     }
  57.     public static void main(String[] args) {
  58.         int testTime = 500000;
  59.         int maxSize = 10;
  60.         int maxValue = 100;
  61.         boolean succeed = true;
  62.         for (int i = 0; i < testTime; i++) {
  63.             int[] arr = generateRandomArray(maxSize, maxValue);
  64.             Arrays.sort(arr);
  65.             int value = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
  66.             if (test(arr, value) != nearestIndex(arr, value)) {
  67.                 printArray(arr);
  68.                 System.out.println(value);
  69.                 System.out.println(test(arr, value));
  70.                 System.out.println(nearestIndex(arr, value));
  71.                 succeed = false;
  72.                 break;
  73.             }
  74.         }
  75.         System.out.println(succeed ? "Nice!" : "Fucking fucked!");
  76.     }
  78. }

一个有序数组中，找<=某个数最右侧的位置

局部最小值问题

  1. 单独看0位置是不是小于1位置，是就是局部最小
  2. 单独看n-1位置是不是小于n-2位置，是就是局部最小
  3. 假如上面两个都没有满足那么趋势是这样的情况 \…………/ ，中间怎么变化不知道，但必然有局部最小值

二分局部最小值-min.gif

  1. 先看中点位置，假如mid两边都比mid大，那么返回mid
  2. 如果不成立（从1到n-2二分）
    1. 假如mid的左边比mid小，而右边比mid大，那么 \……/mid/……/ ，则左侧必然存在局部最小，右边不确定，砍掉右侧，保留左侧
    2. 假如mid的左边比mid大，而右边比mid小，那么 \……\mid\……/ ，则右侧必然存在局部最小，左边不确定，砍掉左侧，保留右侧
    3. 假如mid的左边比mid大且右边比mid大，那么 \……/mid\……/ ，则两侧都必然存在局部最小，这时随便砍掉一侧，保留一侧即可
    4. 假如mid的左边比mid小，而右边比mid小，那么 \……\mid/……/ ，则mid就是局部最小值，此时返回mid即得结果（下图中的高度代表大小）

二分局部最小值讨论-min.gif

  1. 左右都小时（即mid比左右都大时），选左选右都可以，只要找到一个即可，不需要判断谁更小了
  1. package class01;
  3. public class Code06_BSAwesome {
  5.     public static int getLessIndex(int[] arr) {
  6.         if (arr == null || arr.length == 0) {
  7.             return -1; // no exist
  8.         }
  9.         if (arr.length == 1 || arr[0] < arr[1]) {
  10.             return 0;
  11.         }
  12.         if (arr[arr.length - 1] < arr[arr.length - 2]) {
  13.             return arr.length - 1;
  14.         }
  15.         int left = 1;
  16.         int right = arr.length - 2;
  17.         int mid = 0;
  18.         while (left < right) {
  19.             mid = (left + right) / 2;
  21.             if (arr[mid] > arr[mid - 1]) {
  22.                 // 左右都小和左小右大的情况走这个分支
  23.                 right = mid - 1;
  24.             } else if (arr[mid] > arr[mid + 1]) {
  25.                 // 左大右小的情况走这个分支
  26.                 left = mid + 1;
  27.             } else {
  28.                 // 左右都大时走这个分支，即找到局部最小值了===>结束
  29.                 return mid;
  30.             }
  31.         }
  32.         return left;
  33.     }
  35. }