课程ppt

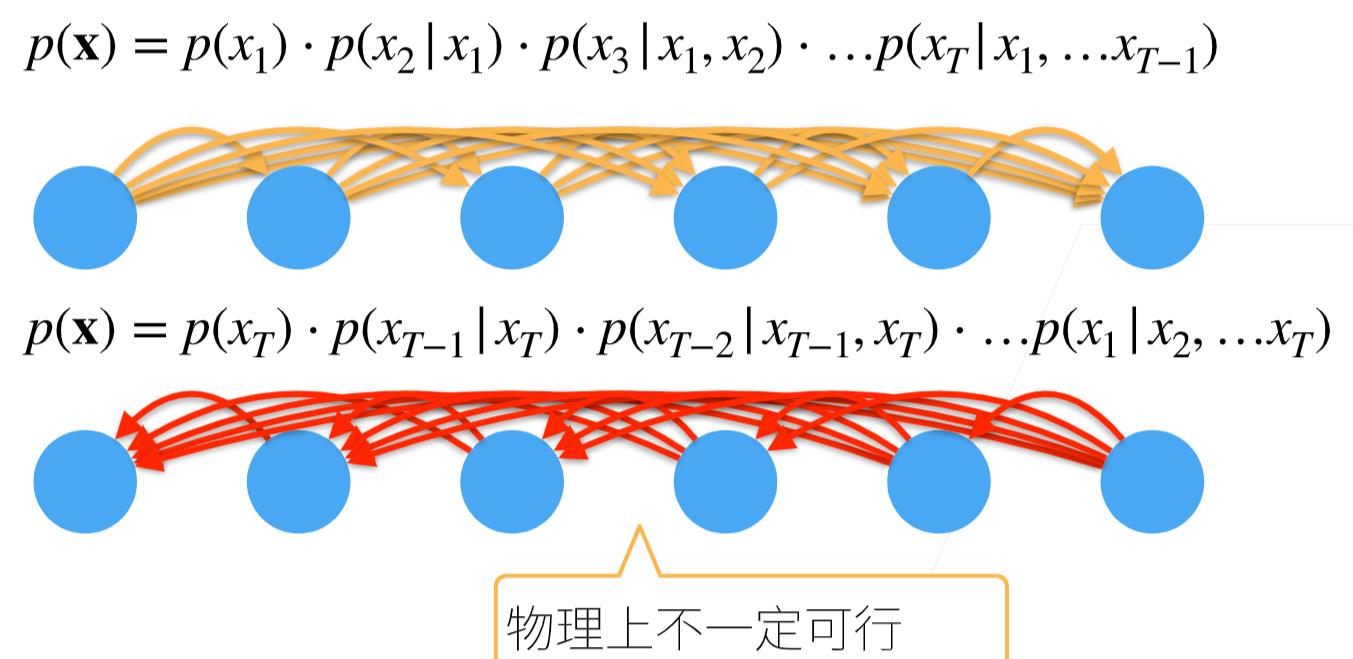
image.png
image.png
对见过的数据建模，也称自回归模型
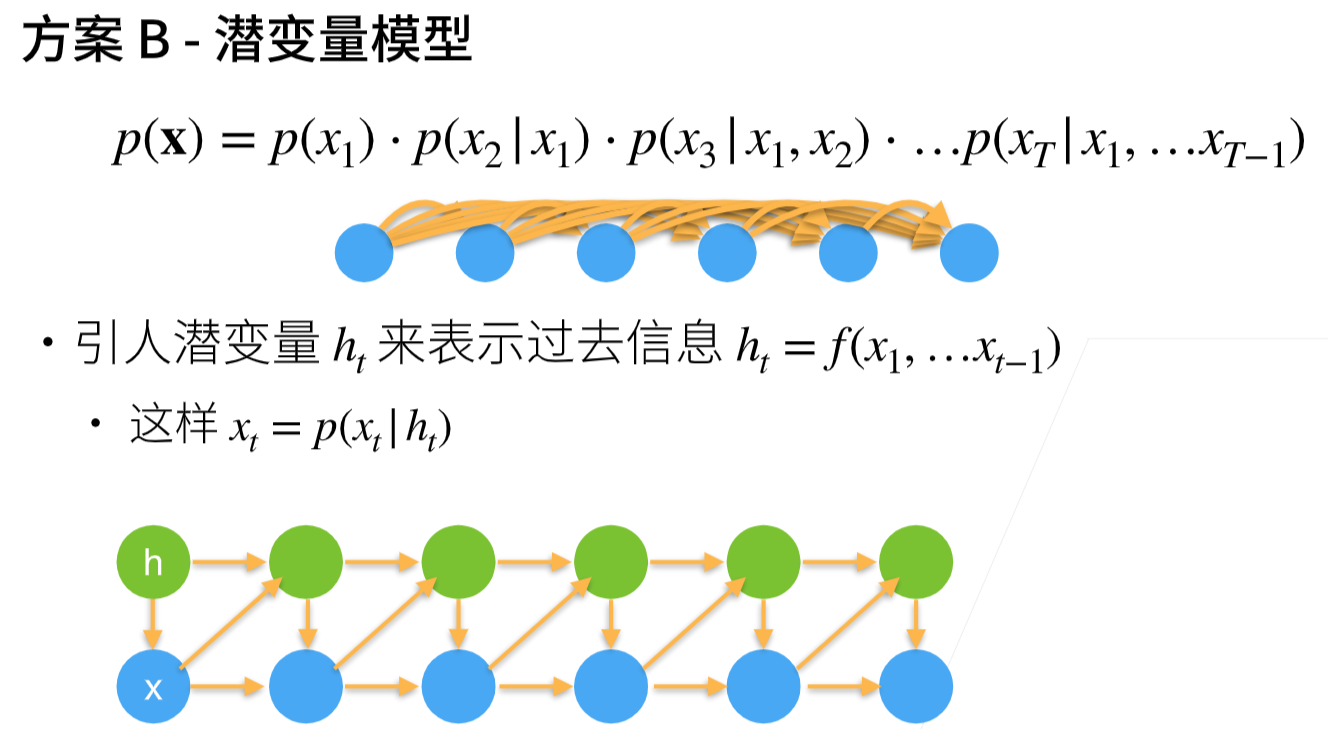
image.png

引入潜变量ht来表示过去信息，ht = f(x1,x2,…,xt-1)
xt = p(xt|ht)

模型1：
x’ 和前一个时间的x和潜变量h’有关
模型2：
h’和前一个时间的x和前一个时间的潜变量h有关

image.png
总结：

  • 时序模型中，当前数据跟之前观察到的数据相关
  • 自回归模型使用自身过去数据来预测未来
  • 马尔可夫模型假设当前只跟最近少数数据相关，从而简化模型
  • 潜变量模型使用潜变量来概括历史信息

part-3_1.pdf

代码

labels = x[tau:].reshape((-1, 1))
这里-1是指未设定行数，程序随机分配，所以这里-1表示任一正整数
所以reshape(-1,1)表示（任意行，1列）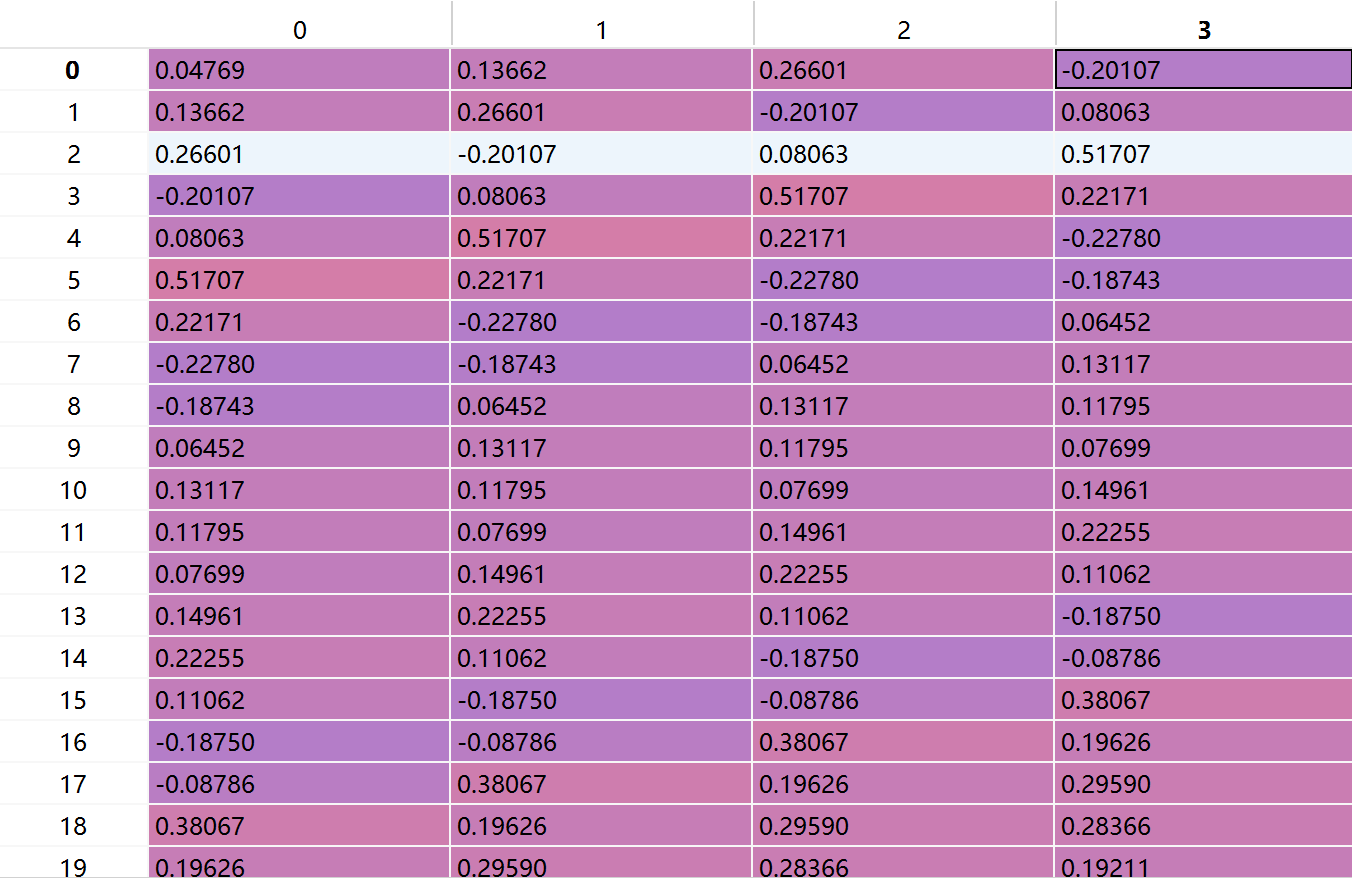
image.png

  1. import torch
  2. from torch import nn
  3. from d2l import torch as d2l
  5. # 序列模型
  6. # 使用正弦函数和一些可加性噪声来生成序列数据，时间步为1，2，..., 1000
  8. T = 1000
  9. time = torch.arange(1,T+1,dtype=torch.float32)
  10. x = torch.sin(0.01*time)+torch.normal(0,0.2,(T,))
  11. d2l.plot(time,[x],'time','x',xlim=[1,1000],figsize=(6,3))
  15. tau = 4
  16. features = torch.zeros((T - tau, tau))
  17. for i in range(tau):
  18.     features[:, i] = x[i:T - tau + i]
  20. labels = x[tau:].reshape((-1, 1))
  22. batch_size, n_train = 16, 600
  23. train_iter = d2l.load_array((features[:n_train], labels[:n_train]),
  24.                             batch_size, is_train=True)
  27. ### 使用一个相当简单的结构：只是一个拥有两个全连接层的多层感知机
  29. def init_weights(m):
  30.     if type(m) == nn.Linear:
  31.         nn.init.xavier_uniform_(m.weight)
  32. def get_net():
  33.     net = nn.Sequential(nn.Linear(4,10),nn.ReLU(),nn.Linear(10,1))
  34.     net.apply(init_weights)
  35.     return net
  37. loss = nn.MSELoss()
  40. def train(net,train_iter,loss,epochs,lr):
  41.     trainer = torch.optim.Adam(net.parameters(),lr)
  42.     for epoch in range(epochs):
  43.         for X,y in train_iter:
  44.             trainer.zero_grad() #梯度设为0
  45.             l = loss(net(X),y)
  46.             l.backward()
  47.             trainer.step()
  48.         print(f'epoch {epoch+1},'
  49.              f'loss {d2l.evaluate_loss(net,train_iter,loss)}')
  51. net = get_net()
  52. train(net,train_iter,loss,5,0.01)
  54. ### 模型预测下一个时间步
  55. onestep_preds = net(features)
  56. d2l.plot(
  57.     [time,time[tau:]],
  58.     [x.detach().numpy(),onestep_preds.detach().numpy()],
  59.     'time','x',
  60.     legend=['data','1-step preds'],
  61.            xlim=[1,1000],figsize=(6,3)
  62. )