Variable

Variable和Tensor本质上没有区别，不过Variable会被放入一个计算图中，然后进行前向传播，反向传播，自动求导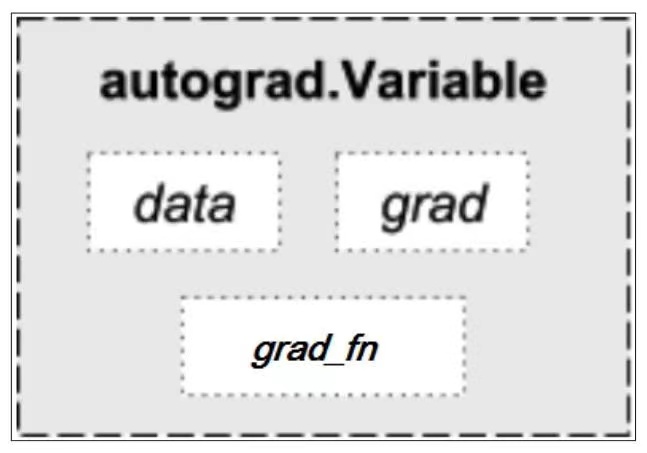

Variable有三个比较重要的属性：data, grad, grad_fn
通过data可以取出Variable里面tensor数值，
grad_fn表示的是得到这个Variable的操作，比如是加减还是乘除来得到的
gard是这个Variable的方向传播梯度

The Variable API has been deprecated: Variables are no longer necessary to use autograd with tensors. Autograd automatically supports Tensors with requires_grad set to True.
在最新的pytorh版本中已经被弃用

Pytorch自动求导机制

PyTorch会根据计算过程来自动生成动态图，然后可以根据动态图的创建过程进行反向传播，计算得到每个节点的梯度值。
为了能够记录张量的梯度，首先需要在创建张量的时候设置一个参数requires_grad = True, 意味着这个张量将会加入到计算图中，作为计算图的叶子节点参与计算，通过一系列的计算，最后输出结果张量，也就是节点。
几乎所有的张量创建方式都可以指定requires_grad=True这个参数，在后续的计算中得到的中间结果的张量都会被设置成requires_grad=True。
对于pytorch来说，每个张量都有一个grad_fn方法，这个方法包含着创建该张量的运算的导数信息。在反向传播过程中，通过传入后一层神经网络的梯度，该函数会计算出参与运算的所有张量的梯度。

自动求导机制实例

张量绑定的梯度张量在不清空的情况下会逐渐积累，这种特性在某些情况下是有用的，比如，需要一次性求很多迷你批次的累积梯度，但在一般情况下，不需要用到这个特性，所以要注意将张量的梯度清零。

计算图构建的启用和禁用

由于计算图的构建需要消耗内存和计算资源，在一些情况下，计算图并不是必要的，比如神经网络的推导。
在这种情况下，可以使用**torch.no_grad**上下文管理器，在这个上下文管理器的作用域进行的神经网络计算不会构建任何计算图。

另外还有一种情况是对于一个张量，我们在反向传播的时候可能不需要让梯度通过这个张量的节点，也就是新建的计算图要和原来的计算图分离，在这种情况下，可以使用张量的**detach**方法，通过调用这个方法，可以返回一个新的张量，该张量会为一个新的计算图的叶子节点，新的计算图和老的计算图相互分离，互不影响。

计算图

计算图是一种有向无环图像，用图形方式来表示算子与变量之间的关系
如表达式: z = wx +b
可以表示为：y=wx , z = y+b
其中x,w,b为变量，是用户创建的变量，不依赖于其他变量，故又称为叶子节点。
为了计算各叶子节点的梯度，需要把对应的张量参数requires_grad属性设置为True,这样就可以跟踪其历史记录
y, z 是计算得到的变量，非叶子节点
z为根节点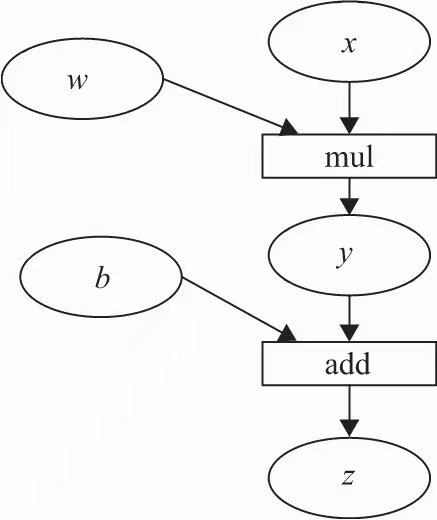

目标是更新各叶子节点的梯度，根据复合函数求导的链式法则：

PyTorch调用backward()方法，将自动计算各节点的梯度，这是一个反向传播过程
autograd沿着图2-10，从当前根节点z反向溯源，利用导数的链式法则，计算所有叶子节点的梯度，其梯度值累加到grad属性中。
对非叶子节点的计算操作记录在grad_fn中，叶子节点的grad_fn为None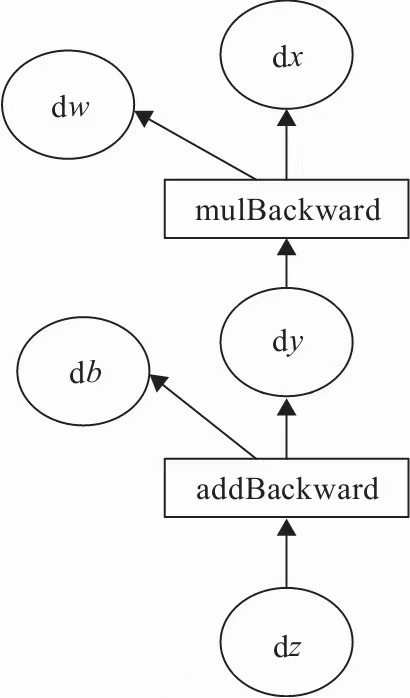

自动求导要点

1. 创建叶子节点的Tensor, 使用requires_grad参数指定是否对其的操作，以便之后利用backward()方法进行梯度求解。
2. 可利用requires_grad()方法修改Tensor的requires_grad属性。可以调用detach()或 with torch.no_grad(): ,将不再计算张量的梯度，跟踪张量的历史记录。这点在评估模型、测试模型阶段经常用到，