多元线性回归

我们使用 mtcars 数据集来演示。

  1. library(dplyr)
  2. df <- mtcars %>% select(-c(am, vs, cyl, gear, carb))
  3. View(df)
  1. 连续变量
    例如我们相同其中几个变量（disp ，hp ，dra，twt）来预测 mpg。
  1. model <- mpg ~ disp + hp + drat + wt
  2. fit <- lm(model, df)
  3. fit
  1. ## Call:
  2. ## lm(formula = model, data = df)
  3. ##
  4. ## Coefficients:
  5. ## (Intercept)         disp           hp         drat           wt  
  6. ## 29.148738     0.003815    -0.034784     1.768049    -3.479668

也可以通过下面方式查看更多细节

  1. summary(fit)
  2. anova(fit)

可视化

  1. par(mfrow=c(2,2))
  2. plot(fit)

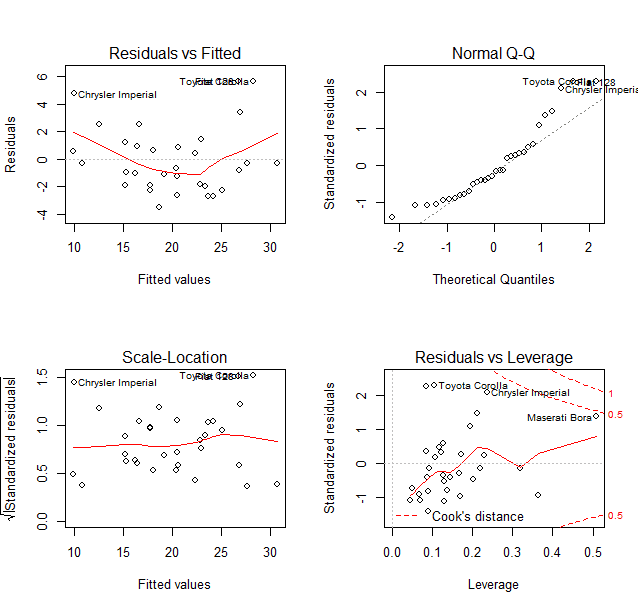
R 多元线性回归和逐步回归 - 图1

  1. 因子型变量
  1. model <- mpg~ disp + hp + drat + wt + cyl + vs+ am+ gear + carb
  2. df <- mtcars %>%
  3.   mutate(cyl = factor(cyl),
  4.          vs = factor(vs),
  5.          am = factor(am),
  6.          gear = factor(gear),
  7.          carb = factor(carb))
  8. summary(lm(model, df))

逐步回归

目的是筛选出最佳变量，更好拟合。下面是使用olsrr包自动筛选所有变量。

  1. library(dplyr)
  2. library(olsrr)
  4. df <- mtcars %>%
  5.   mutate(cyl = factor(cyl),
  6.          vs = factor(vs),
  7.          am = factor(am),
  8.          gear = factor(gear),
  9.          carb = factor(carb))
  11. model <- mpg~.
  12. fit <- lm(model, df)
  13. test <- ols_step_all_possible(fit)
  14. plot(test)

test结果中会给出所有变量组合，并给出了拟合度 rsquare 值。

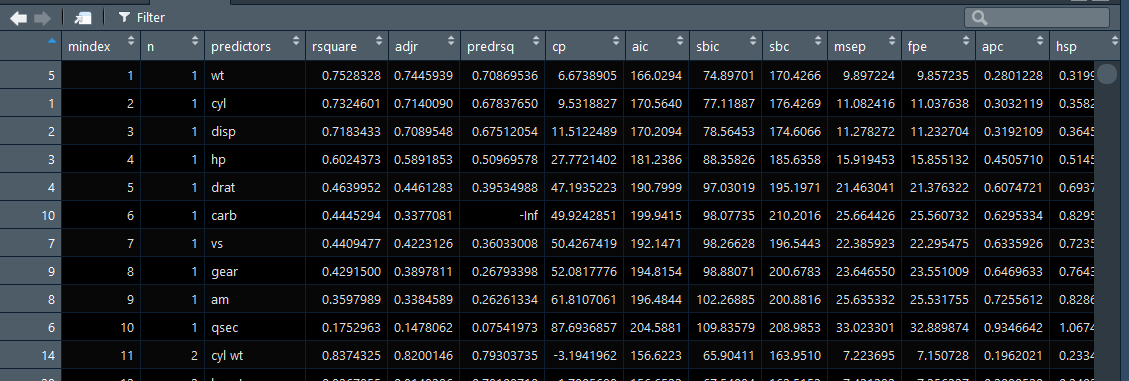
R 多元线性回归和逐步回归 - 图2

R-squared（值范围0-1）描述的 输入变量对输出变量的解释程度。在单变量线性回归中R-squared 越大，说明拟合程度越好。然而只要曾加了更多的变量，无论增加的变量是否和输出变量存在关系，则R-squared 要么保持不变，要么增加。So, 需要adjusted R-squared ,它会对那些增加的且不会改善模型效果的变量增加一个惩罚向。结论，如果单变量线性回归，则使用 R-squared评估，多变量，则使用adjusted R-squared。在单变量线性回归中，R-squared和adjusted R-squared是一致的。另外，如果增加更多无意义的变量，则R-squared 和adjusted R-squared之间的差距会越来越大，Adjusted R-squared会下降。但是如果加入的特征值是显著的，则adjusted R-squared也会上升。
作者：王发北
来源：CSDN
原文：https://blog.csdn.net/wwangfabei1989/article/details/80656668
版权声明：本文为博主原创文章，转载请附上博文链接！

下面我去试验下

我有65个变量，用这种方法需要多久，毕竟计算所有组合是很大的，我用服务器试一下，emmm
如果不行可要换其他回归策略了

试验结果

我宛如智障，一种排列组合C(65,33) = 3609714217008131600，更别说其他情况一起累加了，结果太大直接无法写入了，看下报错
R 多元线性回归和逐步回归 - 图3
当然有其他挑选变量的办法，有向前回归，向后回归和逐步回归，也有许多R包可以实现。我采用逐步回归，试了 MASS 包中的 stepAIC(fit, direction = “both”) 和 olsrr 包中的 ols_step_both_aic(fit)，结果一致。

参考